O Cone é uma das figuras que costuma aparecer nas questões de vestibulares! É importante saber sua definição, suas fórmulas, seus elementos e origem. Leia o resumo e treine seus conhecimentos com os exercícios sobre Cone. Ao final, haverá um gabarito para confirmar suas respostas!
Quer seguir diretamente para alguma parte? Clique em um dos tópicos abaixo:
- Definição: o que são Cones?
- Quais são os principais elementos do Cone?
- Fórmulas das Áreas e Volumes do Cone.
- Os 10 melhores exercícios sobre Cone!
- Gabarito das questões sobre Cone.
Quando você terminar os exercícios de Cone, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil!
Definição: o que é um Cone?
O Cone é um sólido geométrico do tipo corpo redondo. Sua principal característica é ter uma única base circular de onde saem segmentos de reta que se unem em um único vértice logo acima.
Em outras palavras, seu formato é semelhante ao de uma pirâmide, só que com a base e o corpo arredondados.
Simples não é? Mas não para por aí…
É preciso conhecer seus elementos, suas fórmulas, entender as seções e os seus tipos. Só com todas essas informações é que conseguimos resolver os exercícios!
- Fizemos um artigo COMPLETO sobre o Cone, sua planificação, secções, tipos e muito mais!
Quais são os principais componentes do Cone?
Entender as definições é uma tarefa trabalhosa, mas conhecer os componentes do Cone vai te ajudar a entendê-lo. São eles:
- Base: no caso do cone, é um plano em que está a circunferência. Ela é uma superfície reta, ou seja, quando passamos a mão sentimos que está “liso”.
- Raio (r): o raio da base do cone é a distância entre o centro do cone e a sua face externa.
- Diâmetro (D): é a medida que liga as duas extremidades do círculo da base, passando pelo centro. Na prática, vale o dobro do raio (2r).
- Altura (h): é, literalmente, quanto mede a altura do cone. Na geometria, definimos como um segmento que liga o vértice superior à superfície da base, fazendo um ângulo de 90°.
- Eixo: é o segmento de reta que liga o vértice ao centro da base. Em alguns tipos de cone, ele coincide com a altura.
- Geratriz (g): é o segmento que liga o vértice ao ponto mais externo do círculo da base, só que passando pela superfície do cone. Portanto, não tem o mesmo valor que a altura. Ela é calculada usando pitágoras, junto ao raio e a altura.
- O Cone possui 2 faces (uma base e toda a parte curva no meio), 1 vértice e 1 aresta.
São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
Quais são as Fórmulas do Cone?
- Área da base:
Ab = π.r²
Em que:
Ab: área da base
π: 3,14
r: raio
- Área Lateral:
Al = π.r.g
Em que:
Al: área lateral
π: 3,14
r: raio
g: geratriz
- Área Total:
At = Ab + Al
ou
At = (π.r²) + (π.r.g)
Onde:
At: área total
Ab: área da base
Al: área lateral
π: 3,14
r: raio
g: geratriz
- Volume do Cone:
V = (Ab.h) / 3
ou
V = (π.r².h) /3
Onde:
V: volume
Ab: área da base
π: 3,14
r: raio
h: altura
- Volume do Tronco de Cone
V = (πh)/3 . (R² + Rr + r²)
Onde:
V: volume
π: 3,14
r: raio menor
R: raio maior
h: altura
Os 10 exercícios sobre Cone!
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Obrigado por ter lido até aqui!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1- (PUC-MG)
Um monte de areia tem a forma de um cone circular reto, com volume V= 4π m³. Se o raio da base é igual a dois terços da altura desse cone, pode-se afirmar que a medida da altura do monte de areia, em metros, é:
a) 2.
b) 3.
c) 4.
d) 5.
Questão 2- (Cefet-PR)
O raio da base de um cone circular reto mede 3 m e o perímetro de sua seção meridiana mede 16 m. O volume desse cone mede:
a) 8π m³.
b) 10π m³.
c) 14π m³.
d) 12π m³.
e) 36π m³.
- Você já fez 20% das questões sobre Cone. Continue assim!
Questão 3- (PUC-RS)
O raio da base de um cone circular reto e a aresta da base de uma pirâmide quadrangular regular têm a mesma medida. Sabendo que suas alturas medem 4 cm, então a razão entre o volume do cone e o da pirâmide é:
a) 1.
b) 4.
c) 1/π.
d) π.
e) 3π.
Questão 4- (Fuvest 2006)
Um cone circular reto está inscrito em um paralelepípedo reto retângulo, de base quadrada, como mostra a figura.
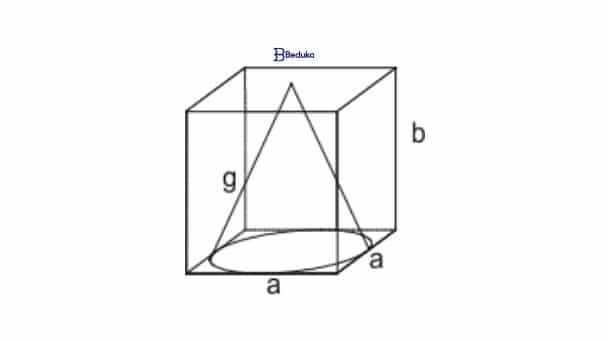
A razão b/a entre as dimensões do paralelepípedo é 3/2 e o volume do cone é π. Então, o comprimento g da geratriz do cone é:
a) 5.
b) 6.
c) 7.
d) 10.
e) 11.
Questão 5- (UECE – adaptada)
Um cone circular reto, cuja medida da altura é h, é secionado por um plano paralelo à base. Assim, formam-se duas partes: um cone menor acima, cuja medida da altura é h/5, e um tronco de cone logo abaixo.
A razão entre as medidas dos volumes do cone maior e do cone menor é:
a) 15.
b) 45.
c) 90.
d) 125.
- Nossa! Você já fez metade das questões de Cone. Vamos lá!
Questão 6- (Cefet- SC)
Dado um copo em forma de cilindro e outro de forma cônica de mesma base e altura. Se eu encher completamente o copo cônico com água e derramar toda essa água no copo cilíndrico, quantas vezes terei que fazê-lo para encher completamente esse copo?
a) Apenas uma vez.
b) Duas vezes.
c) Três vezes.
d) Uma vez e meia.
e) É impossível saber, pois não se sabe o volume de cada sólido.
Questão 7- (Mackenzie)
Um frasco de perfume, que tem a forma de um tronco de cone circular reto de raios 1 cm e 3 cm, está totalmente cheio. Seu conteúdo é despejado em um recipiente que tem a forma de um cilindro circular reto de raio 4 cm, como mostra a figura.
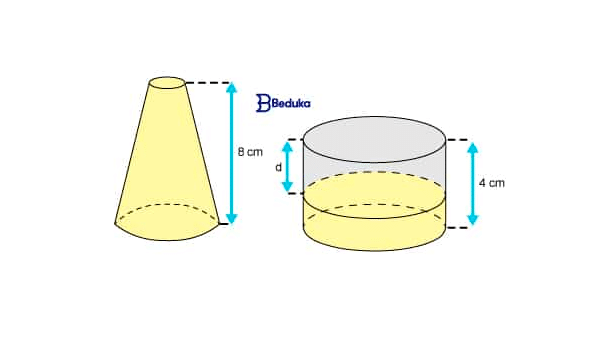
Se d é a altura da parte não preenchida do recipiente cilíndrico e, adotando-se π = 3, o valor de d é:
a) 10/6.
b) 11/6.
c) 12/6.
d) 13/6.
e) 14/6.
Questão 8- (UFRN)
Um abajur em formato de cone equilátero está sobre uma escrivaninha, de modo que, quando aceso, projeta sobre esta um círculo de luz (veja a figura abaixo).
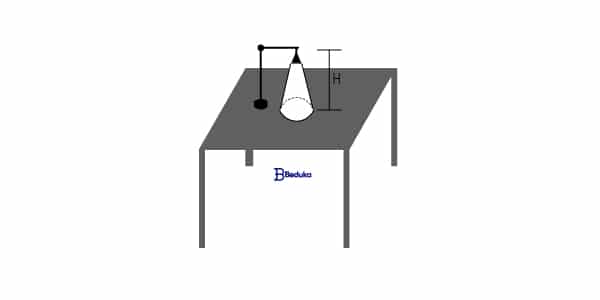
Se a altura do abajur, em relação à mesa, for H = 27 cm, a área do círculo iluminado, em cm2 será igual a:
a) 225π.
b) 243π.
c) 250π.
d) 270π.
- Ufa! Agora só faltam mais dois exercícios de Cone!
Questão 9- (UFG)
A terra retirada na escavação de uma piscina semicircular de 6 m de raio e 1,25 m de profundidade foi amontoada, na forma de um cone circular reto, sobre uma superfície horizontal plana. Admita que a geratriz do cone faça um ângulo de 60° com a vertical e que a terra retirada tenha volume de 20% maior do que o volume da piscina. Nessas condições, a altura do cone, em metros, é de:
a) 2,0.
b) 2,8.
c) 3,0.
d) 3,8.
e) 4,0.
Questão 10 – (Fuvest)
Deseja-se construir um cone circular reto com 4cm de raio da base e 3cm de altura. Para isso, recorta-se, em cartolina, um setor circular para a superfície lateral e um círculo para a base. A medida do ângulo central do setor circular é:
a) 144°.
b) 192°.
c) 240°.
d) 288°.
e) 336°.
- Parabéns, você fez todos os exercícios sobre Cone. Confira agora o Gabarito:
Gabarito das questões sobre Cone
Exercício resolvido da questão 1 –
Alternativa correta: b) 3.
Exercício resolvido da questão 2 –
Alternativa correta: d) 12π m³.
Exercício resolvido da questão 3 –
Alternativa correta: d) π.
Exercício resolvido da questão 4 –
Alternativa correta: d) 10.
Exercício resolvido da questão 5 –
Alternativa correta: d) 125.
Exercício resolvido da questão 6 –
Alternativa correta: c) Três vezes.
Exercício resolvido da questão 7 –
Alternativa correta: b) 11/6.
Exercício resolvido da questão 8 –
Alternativa correta: b) 243π.
Exercício resolvido da questão 9 –
Alternativa correta: c) 3,0.
Exercício resolvido da questão 10 –
Alternativa correta: d) 288°.
- Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos exercícios sobre Cone? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.





