Os 10 melhores exercícios sobre Troncos de Cone e Pirâmide com o Gabarito!

Que a geometria é uma das queridinhas dos vestibulares você já sabe. Inclusive, é normal os alunos conhecerem bem os sólidos geométricos. Mas você domina as fórmulas dos troncos? Leia o resumo para relembrar e treine com os exercícios sobre Troncos de Cone e Pirâmide. Ao final, haverá um gabarito para confirmar suas respostas!

Quer seguir diretamente para alguma parte? Clique em um dos tópicos abaixo:

• Definição: o que são troncos de Cone e Pirâmide?
• Quais são suas fórmulas?
• Lista com os 10 melhores exercícios sobre Troncos!
• Gabarito dos exercícios de Troncos.

Não sabe como organizar seus estudos? Apresentamos o Plano de Estudos Beduka! Com ele, você conseguirá adequar a sua rotina ao seu tempo de aprendizado.

Definição: o que são troncos de Cone e Pirâmide?

Existe uma prática comum na geometria espacial que é a de fazer seções (cortes) nos sólidos geométricos. É como se passássemos uma lâmina em diferentes ângulos para ver qual figura se forma na superfície do corte.

Existem vários possíveis cortes que podemos fazer em um Cone ou em uma Pirâmide. Quando retiramos a “tampa” de um deles, nos restará o seu tronco. 

• São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

Como é um Tronco de Cone?

Quando fazemos a seção transversal no cone, a figura formada na superfície do corte é uma circunferência. Porém, se retirarmos a “tampa” do cone, ou seja, a parte acima do corte, nos restará o tronco de cone.

Assim, a nova figura passa a ter duas bases: uma com círculo menor em cima e outra com um círculo maior embaixo. 

Não confunda com o Cilindro, pois ele mantém o diâmetro constante ao longo do sólido. O tronco de cone não, ele vai “afunilando”. Já já você verá imagens!

Como é um Tronco de Pirâmide?

Quando fazemos a seção transversal na pirâmide, a figura formada na superfície do corte é semelhante à da base. Porém, se retirarmos a “tampa” da pirâmide, ou seja, a parte acima do corte e que contêm o ápex, nos restará o tronco de pirâmide.

Assim, passa a ter duas bases: uma com o polígono menor em cima e outra com o polígono maior embaixo. 

Não confunda com os prismas, pois eles mantêm a apótema da base constante ao longo do sólido. O tronco de pirâmide não, ele vai “afunilando”. Já já você verá imagens!

Quais são as fórmulas do tronco de Cone e de Pirâmide?

A formação de troncos exige que dividamos os sólidos no meio. Ou seja, sempre forma um cone ou pirâmide menor em cima e o tronco abaixo.

Portanto, calcular a área total ou o volume de um tronco é o mesmo que pegar o valor do sólido inicial menos o do sólido menorzinho que se forma em cima.

Simples não é? 

Para isso, você precisa conhecer as fórmulas do Cone e da Pirâmide. 

Não deixe de ler esses dois artigos, mas nós já vamos te ajudar deixando as principais fórmulas aqui:

Como se calcula o Volume do Tronco de Cone?

A fórmula para fazer esse cálculo é a seguinte:

V = (πh)/3 . (R² + Rr + r²)

Onde:

• V: volume.
• π: 3,14.
• r: raio menor.
• R: raio maior.
• h: altura.

Como se calcula o Volume do Tronco de Pirâmide?

Veja a seguir as fórmulas para se calcular o volume do tronco de pirâmide. 

Volume da Pirâmide

V_pir = 1/3 (A_b.h)

Onde:

• V_pir = volume.
• A_b = área da base.
• h = altura.

Volume do Tronco de Pirâmide

V_tronco = V₁ – V₂

Em que:

• V_tronco = volume do tronco da pirâmide.
• V₁ = volume da pirâmide original.
• V₂ = volume da mini pirâmide formada acima do tronco.

Os 10 exercícios sobre Troncos de Cone e Pirâmide!

Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.

Obrigado por ter lido até aqui!

Quando acabar de resolver as atividades, estude para o Enem com o Simulado Beduka. É gratuito e pode ser personalizado com as matérias que você quiser!

Questão 1- (Mackenzie) 

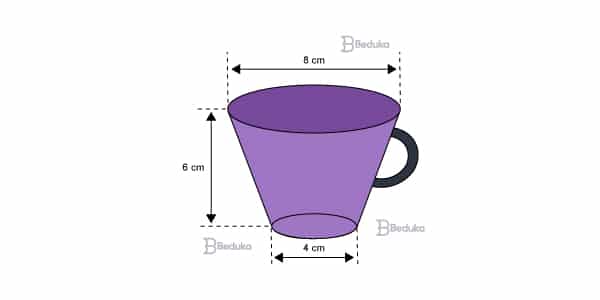
Uma xícara de chá tem a forma de um tronco de cone reto, conforme a figura. Supondo π = 3, o volume máximo de líquido que ela pode conter é:

a) 168 cm³. 

b) 172 cm³.

c) 166 cm³.

d) 176 cm³.

e) 164 cm³.

Questão 2- (FUVEST) 

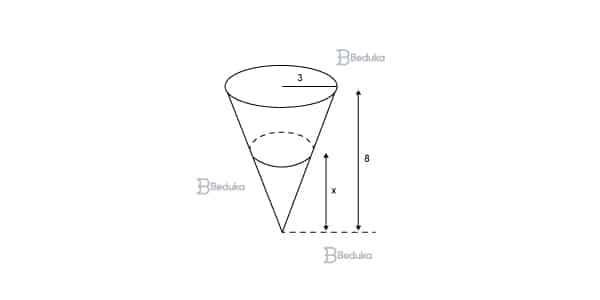
Um copo em forma de cone com altura 8 cm e raio da base 3 cm. Queremos enchê-lo com quantidades iguais de suco e de água. Para que isso seja possível, qual deve ser a altura x atingida pelo primeiro líquido colocado no copo?

a) 8/3 cm.

b) 6 cm.

c) 4 cm.

d) 4√3 cm.

e) 4 ³√4 cm.

• Já chegamos a 20% dos exercícios sobre Troncos de Cone e Pirâmide. Vamos lá!

Questão 3- (Enem)

Na alimentação de gado de corte, o processo de cortar a forragem, colocá-la no solo, compactá-la e protegê-la com uma vedação denomina-se silagem. Os silos mais comuns são os horizontais, cuja forma é a de um prisma reto trapezoidal, conforme mostrado na figura.

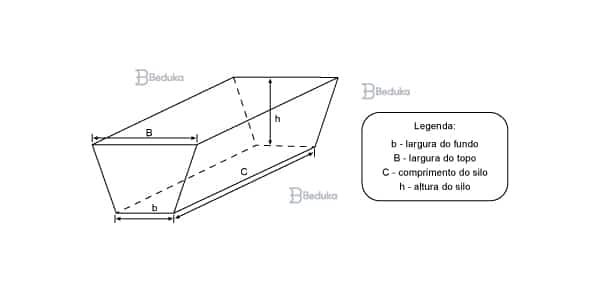
Considere um silo de 2 m de altura, 6 m de largura de topo e 20 m de comprimento. Para cada metro de altura do silo, a largura do topo tem 0,5 m a mais do que a largura do fundo. Após a silagem, 1 tonelada de forragem ocupa 2 m3 desse tipo de silo.

Após a silagem, a quantidade máxima de forragem que cabe no silo, em toneladas, é

a) 110.

b) 125.

c) 130.

d) 220.

e) 260.

Questão 4- (PUC) 

Corta-se uma pirâmide de 12 cm de altura por um plano paralelo à base, distando 4 cm desta. A razão entre a área da base e a área da seção é igual a:

a) 12/7 cm.

b) 7/4 cm.

c) 9/4 cm.

d) 7/9 cm.

e) 9/7cm.

Questão 5- (FATEC) 

Uma pirâmide regular, de 8 cm de altura, tem por base um quadrado cujos lados medem 12 cm. Ela é seccionada por um plano paralelo à base, que intercepta a altura no seu ponto médio. A área total do tronco de pirâmide obtido é, em centímetros quadrados, igual a:

a) 180.

b) 240.

c) 300.

d) 324.

e) 360.

• Você já chegou à metade dos exercícios sobre Troncos de Cone e Pirâmide. Não pare agora!

Questão 6- (PUC) 

Um tronco de pirâmide de bases quadradas tem 21 dm³ de volume. A altura do tronco mede 30 cm e o lado do quadrado de base maior, 40 cm. Então, o lado do quadrado de  base menor mede:

a) 6 cm.

b) 8 cm. 

c) 10 cm.

d) 12 cm.

e) 14 cm.

Questão 7- (Enem)

Em São Paulo, no Parque do Ibirapuera, há um monumento de concreto chamado de Obelisco aos Heróis de 1032, uma homenagem aos que morreram na Revolução Constitucionalista de 1932. Esse monumento tem a forma de um tronco de pirâmide de base quadrada e tem 72m de altura. Suas bases possuem arestas de 9m e 7m.

Determine o custo de concreto utilizado na construção do Obelisco sabendo que o preço do metro cúbico de concreto utilizado na obra é de R$ 250,00.

a) R$ 800.000,00.

b) R$ 1.000.000,00.

c) R$ 1.158.000,00.

d) R$ 1.500.000,00.

e) R$ 2.200.000,00.

Questão 8- (Mackenzie) 

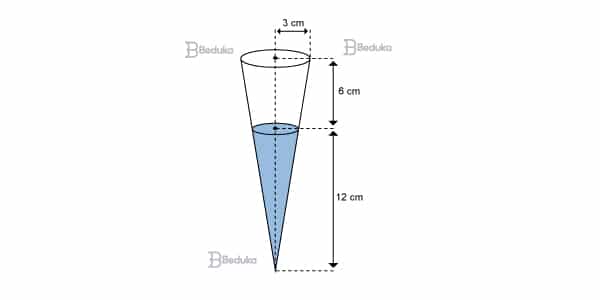
A figura representa o sorvete “choconilha”, cuja embalagem tem a forma de um cone circular reto. O cone é preenchido com sorvete de chocolate até a altura de 12 cm e, o restante, com sorvete de baunilha. Adotando π = 3, o número máximo de sorvetes que é possível embalar, com 2 litros de sorvete de baunilha e 1 litro de sorvete de chocolate, é:

a) 21.

b) 22.

c) 18.

d) 17.

e) 19.

• Ufa! Só faltam mais duas questões sobre Troncos de Cone e Pirâmide. Continue!

Questão 9- (Enem)

Uma empresa precisa comprar uma tampa para o seu reservatório, que tem a forma de um tronco de cone circular reto, conforme mostrado na figura. 

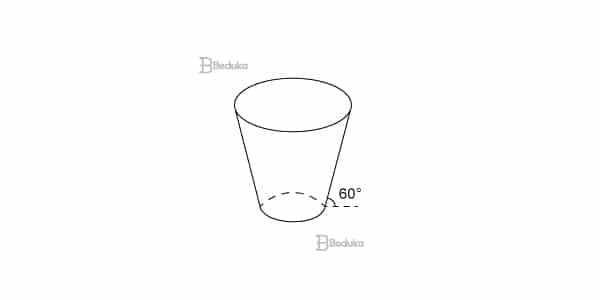
Considere que a base do reservatório tenha raio r = 2√3m e que sua lateral faça um ângulo de 60° com o solo. 

Se a altura do reservatório é 12 m, a tampa a ser comprada deverá cobrir uma área de:

a) 12 m². 

b) 108 m². 

c) (12 + 2√3)²π m².

d) 300π m².

e) (24 + 2√3)²π m².

Questão 10- (USJ-sp) 

Em um tronco de cone, os raios das bases medem 3 cm e 7 cm e a geratriz mede 5 cm. O volume desse tronco em centímetros cúbicos, é:

a) 39π.

b) 49π.

c) 69π.

d) 79π.

e) 58π.

• Parabéns, você fez todos os exercícios de Troncos de Cone e Pirâmide. Confira agora o Gabarito:

Gabarito das questões sobre Troncos de Cone e Pirâmide

Exercício resolvido da questão 1 –

Alternativa correta: a) 168 cm³. 

Exercício resolvido da questão 2 –

Alternativa correta: e) 4 ³√3 cm.

Exercício resolvido da questão 3 –

Alternativa correta: a) 110.

Exercício resolvido da questão 4 –

Alternativa correta: c) 9/4 cm.

Exercício resolvido da questão 5 –

Alternativa correta: e) 360.

Exercício resolvido da questão 6 –

Alternativa correta: c) 10 cm.

Exercício resolvido da questão 7 –

Alternativa correta: c) R$ 1.158.000,00.

Exercício resolvido da questão 8 –

Alternativa correta: d) 17.

Exercício resolvido da questão 9 –

Alternativa correta: b) 108 m². 

Exercício resolvido da questão 10 –

Alternativa correta: d) 79π.

Gostou dos nossos exercícios sobre Troncos de Cone e Pirâmide? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.