A humanidade sempre foi maravilhada com as Pirâmides do Egito. Inclusive, esse sólido é um dos poliedros mais versáteis da geometria, pois sua base pode ter vários formatos. Isso também influencia no cálculo da área, do volume, etc. Aprenda tudo sobre Pirâmides no nosso artigo e desvende seus mistérios!
Neste resumo sobre Pirâmides, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:
- Introdução: O que é a Geometria Espacial?
- Definição: o que é uma Pirâmide?
- Quais são os elementos da Pirâmide?
- Quais são os tipos de Pirâmide?
- Origem da Pirâmide: Planificação.
- Como são as Seções Transversais e Meridionais?
- O que é o Tronco de Pirâmide?
- Fórmulas da Pirâmide e de seu tronco: áreas e volumes.
Depois você pode testar o que aprendeu. É só fazer o nosso Simulado ENEM gratuito! Ele pode ser personalizado com as matérias que você quiser.
Introdução: o que é a Geometria Espacial?
A Geometria Espacial é a área da matemática que estuda os sólidos geométricos. Estamos falando daquelas formas que construímos com 3 dimensões (3D): altura, largura e profundidade.
Quando pegamos um sólido (que é tridimensional), é preciso girar em várias posições para tatear toda a sua superfície. Quando pegamos uma figura plana, existe uma só superfície.
Os sólidos podem ser classificados em poliedros (faces, arestas e vértices, tudo retinho) ou corpos redondos (possuem alguma superfície curva).
Hoje nós vamos falar da Pirâmide, que é um poliedro. Isso significa que ele pertence ao grupo dos que não “rolam”.
Antes de continuar, vale a pena lembrar da Geometria Plana, a parte que estuda as figuras 2D (largura e altura). É nela que estudamos os conceitos básicos (reta, linha, ponto, plano, altura, etc.) que também usaremos adiante.
Definição da geometria: o que é uma Pirâmide?
Uma pirâmide é um sólido geométrico do tipo poliedro, ou seja, não possui superfície curva. Elas sempre tem uma ponta em cima, de onde partem segmentos de reta até a base onde está apoiada. Sua base pode ter diferentes formatos!
Na verdade, quase todo mundo já viu e ficou fascinado com as pirâmides do Egito, que representam fielmente este sólido!
Agora que já entendemos a definição simples, vamos entender uma mais formal e matemática:
“Seja um plano α, um ponto V, de forma que V ∉ α, uma área poligonal S no plano α, chamamos de pirâmide a união dos segmentos de retas VP onde P ∈ S.”
- São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
Quais são os principais elementos da Pirâmide?
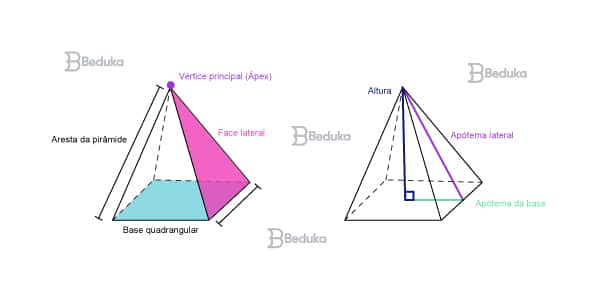
Entender as definições são tarefas trabalhosas, mas conhecer os componentes da Pirâmide vai te ajudar a entendê-la. São eles:
- Faces: são os “lados” ou “paredes” do sólido. Ela é uma superfície reta, ou seja, quando passamos a mão sentimos que está “liso”. Na matemática, são os diferentes planos que compõem a figura.
- Arestas: são os segmentos de reta que unem as faces. Podem ser classificadas em arestas da base (os lados do polígono da base) e arestas laterais (segmentos que unem o vértice superior da pirâmide até sua base).
- Vértice: são as “quinas” ou “pontas” da figura, o encontro entre duas arestas. É interessante notar que a pirâmide tem um vértice único na parte superior, chamado especificamente de ápex.
- Base: é o plano (ou face) em que o sólido está apoiado. No caso das pirâmides, há apenas 1 base e elas podem ter diversos formatos (triângulo, quadrado, etc.).
- Altura (h): é, literalmente, quanto mede a altura do sólido. Na geometria, definimos como um segmento de reta que liga o ápex até superfície da base, fazendo um ângulo de 90°.
- Eixo: é o segmento de reta que liga o vértice ao centro da base. Na maioria das pirâmides, ele coincide com a altura. Adiante, veremos um exemplo de quando isso não acontece.
- Apótema da pirâmide: é o segmento que liga o ápex até a base, passando pela face lateral. Ou seja, corresponde à altura de cada face lateral.
- Apótema da base: é o segmento que une o centro da base até uma de suas extremidades. Se a base fosse circular, diríamos ser o raio. Mas não é, portanto, cada polígono da base terá a sua própria apótema.
Quais são os tipos de Pirâmides e seus nomes?
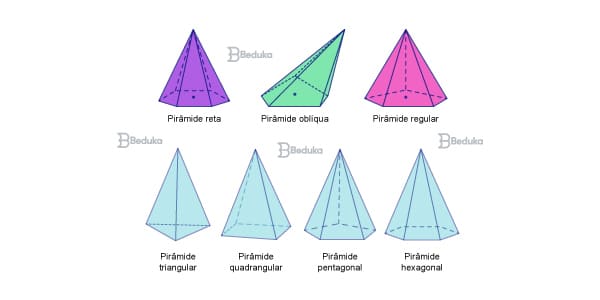
Como já demos o spoiler antes, você já imagina que há diferentes formatos de pirâmides. Eles dependem da inclinação de seu eixo, da relação entre suas medidas e do formato da base.
Conforme a inclinação
- Pirâmide Reta: quando o eixo e a altura são perpendiculares à base (formam um ângulo de 90º) e todas as apótemas são congruentes (têm o mesmo valor).
- Pirâmide Oblíqua: quando o eixo não é perpendicular à base da figura. Assim, algumas apótemas são maiores que as outras.
Conforme a base
- Pirâmide Triangular: sua base é um triângulo. Então, este sólido terá quatro faces: três faces laterais triangulares e a face da base, também triangular.
- Pirâmide Quadrangular: sua base é um quadrado ou retângulo. Então, terá cinco faces: quatro laterais triangulares e a face da base quadrangular.
- Pirâmide Pentagonal: sua base é um pentágono. Então, terá seis faces: cinco faces laterais triangulares e a face da base pentagonal.
- Pirâmide Hexagonal: sua base é um hexágono. Então, será composta por sete faces: seis faces laterais triangulares e face da base hexagonal.
Observe que o número de lados do polígono da base corresponde ao número de faces laterais da pirâmide. Então, as faces totais sempre serão o número de lados da base + 1.
Inclusive, as bases mudam de formado, mas as faces laterais sempre serão triangulares.
Conforme a relação entre suas medidas
Por fim, há as Pirâmides Regulares, caracterizadas por:
- A base é um polígono regular;
- A projeção ortogonal do vértice é o centro desse polígono.
- Todas as arestas laterais possuem a mesma medida;
- Todas as apótemas possuem a mesma medida;
- Todas as faces laterais são congruentes.
As irregulares não obedecem a todos esses padrões ao mesmo tempo.
Como criamos uma Pirâmide? Planificação!
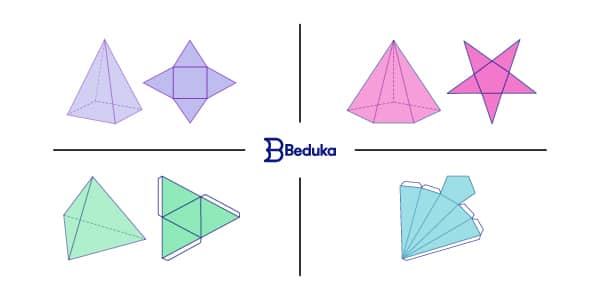
Na infância, é comum as escolas pedirem que os alunos façam sólidos geométricos. Você já fez isso, não fez?
O que os professores nos pedem é, justamente, montar o sólido a partir de sua planificação. Assim, a planificação é a tentativa de representar todas as partes dos sólidos em duas dimensões.
Para conseguir, é preciso ter boa visão espacial. Isso significa olhar para o conjunto de figuras planas e imaginar que você tirou do papel, cortou, dobrou, colou e conseguiu formar um sólido.
No caso da pirâmide, as planificações são formadas sempre por um polígono e vários triângulos, conforme o número de lados desse polígono. O polígono será a base, enquanto os triângulos formarão a superfície lateral.
Como são as Seções na Pirâmide?
Existe uma prática comum na geometria espacial que é a de fazer seções (cortes) nos sólidos. É como se passássemos uma lâmina em diferentes ângulos para ver qual figura se forma na superfície do corte.
Existem vários possíveis cortes que podemos fazer. Veja:
- Secção Meridional: é a intersecção entre o sólido e um plano vertical (contém o eixo). A figura formada em uma pirâmide sempre será um triângulo.
- Secção Transversal: é a intersecção entre o sólido e um plano horizontal (paralelo às bases). A figura formada em uma pirâmide sempre será um polígono de mesmo formato que a base, só que em dimensões menores.
O que é o Tronco de Pirâmide?
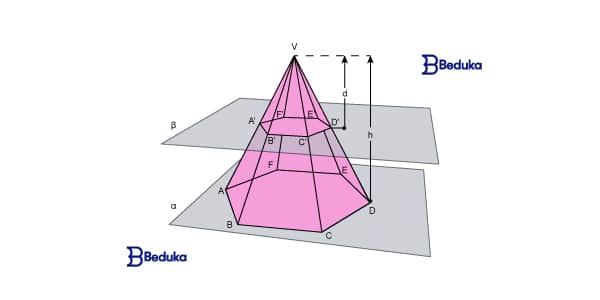
Quando fazemos a seção transversal na pirâmide, a figura formada na superfície do corte é semelhante à da base. Porém, se retirarmos a “tampa” da pirâmide, ou seja, a parte acima do corte e que contêm o ápex, nos restará o tronco de pirâmide.
Assim, passa a ter duas bases: uma com o polígono menor em cima e outra com o polígono maior embaixo. Não confunda com os prismas, pois eles mantêm a apótema da base constante ao longo do sólido. O tronco de pirâmide não.Ele vai “afunilando”.
A fórmula de seu volume é diferente, mostraremos no último tópico desse texto!
Como calcular área e volume da Pirâmide?
Ao lidar com sólidos geométricos, podemos calcular:
- Área da base: valor do preenchimento da superfície das bases.
- Área lateral: valor do preenchimento da superfície que “rola”.
- Área total: soma das duas anteriores.
- Volume: o preenchimento interno do sólido, como o quanto de água que cabe dentro.
Vamos conhecer as fórmulas para calcular as áreas e o volume da Pirâmide:
Fórmula das áreas da Pirâmide
- Área da base: depende do polígono que a formar.
Atri = (b.h) / 2
Aquad = b.h
Apent = P.a ou 5.l.a
Ahex = (P.a) / 2 ou 6 (l.√3) / 2
Em que:
Atri = Área do triângulo.
Aquad = Área de quadriláteros.
Apent = Área do pentágono.
Ahex = Área do hexágono.
b = base do triângulo.
h = altura do triângulo.
P = perímetro da base.
a = apótema da base.
l = lado da base.
- Área Lateral: sempre serão triângulos, tantos quanto o número de lados da base.
Al = n(b.h) / 2
Em que:
Al: área lateral.
n: número de lados da base ou número de faces laterais.
b: base do triângulo.
h: altura do triângulo.
- Área Total: é a soma da área da base e da área lateral.
At = Ab + Al
Em que:
At: área total.
Ab: área da base.
Al: área lateral.
Fórmula do Volume da Pirâmide
O volume de qualquer sólido com uma base e uma ponta em cima, seja poligonal ou corpo redondo, é dado por ⅓ do produto da área da base pela altura.
- Volume da Pirâmide:
Vpir = 1/3 (Ab.h)
Onde:
Vpir = volume.
Ab = área da base.
h = altura.
- Volume do Tronco de Pirâmide
Vtronco = V1 – V2
Em que:
Vtronco = volume do tronco da pirâmide.
V1 = volume da pirâmide original.
V2 = volume da mini pirâmide formada acima do tronco.
Gostou do nosso resumo com tudo sobre Pirâmide? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





