A Geometria Espacial é a área que estuda os sólidos geométricos, ou seja, aqueles que possuem três dimensões e não “cabem” no papel. Além de calcular a área, aprendemos uma novidade: como encontrar o volume. Neste resumo, você aprende tudo o que é importante saber: definições, exemplos e fórmulas.
Neste artigo sobre Geometria Espacial você encontrará todos os tópicos abaixo. Clique em um deles para ir direto ao assunto!
- O que é Geometria Espacial?
- Quais são as formas geométricas espaciais e seus tipos?
- A importante Relação de Euler!
- Para que serve o estudo da geometria espacial?
- Como calcular área total e volume dos sólidos?
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que é Geometria Espacial?
A Geometria Espacial é a área da matemática que estuda os sólidos geométricos. Esses são as formas que construímos com 3 dimensões: altura, largura e profundidade.
Por isso, surge a novidade de calcular não só a área total, mas também o volume do sólido.
Você já deve ter ouvido falar em Geometria Plana, que estuda as figuras 2D (como uma folha de papel, tem largura e altura). Apesar de diferentes, é importante compreendê-la para depois avançarmos à Geometria Espacial.
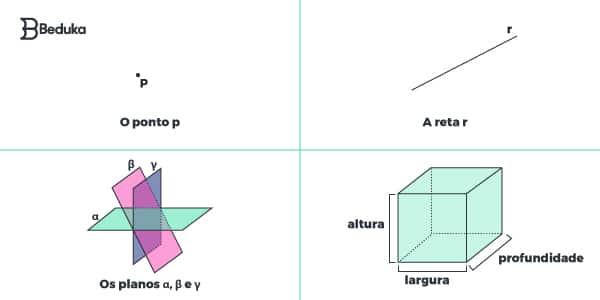
Os conceitos básicos de qualquer geometria são os mesmos: reta, ponto, plano. Vamos relembrá-los:
- Ponto: é aquilo que não tem partes, indivisível. Ele marca posição no espaço, junto às coordenadas.
- Reta: é um segmento infinito composto por pontos lineares, também é definida como a distância entre, no mínimo, 2 pontos.
- Linha: é semelhante à reta, mas tem a propriedade de formar curvas e nós sobre si mesma.
- Plano: é uma estrutura infinita que se estende em todas as direções, e cada plano determina uma medida: a altura pertence a um plano, o comprimento a outro e a profundidade a outro.
- Espaço: é a união dos 3 planos, o que garante o “efeito 3d”.
Ainda é importante relembrar alguns termos e relações entre esses elementos, porque eles podem aparecer em questões e explicações:
- Os pontos ainda podem ser coplanares quando pertencem ao mesmo plano e colineares quando pertencem a uma mesma linha.
- Quando as retas pertencem ao mesmo plano, elas podem ser paralelas, concorrentes ou coincidentes. Contudo, se não forem coplanares, elas serão chamadas de reversas.
- Já os planos, quando são paralelos, não compartilham nenhum ponto em comum. Quando eles se interceptam de alguma forma, são chamados de secantes, e quando há dois ocupando o mesmo espaço, são chamados de coincidentes.
- Por último, também podemos relacionar retas e planos, lembrando que elas podem pertencer ao plano, serem secantes (apenas tocá-lo em um ponto) ou serem paralelas (quando não possuem nada em comum).
Quais são as formas geométricas espaciais e seus tipos?
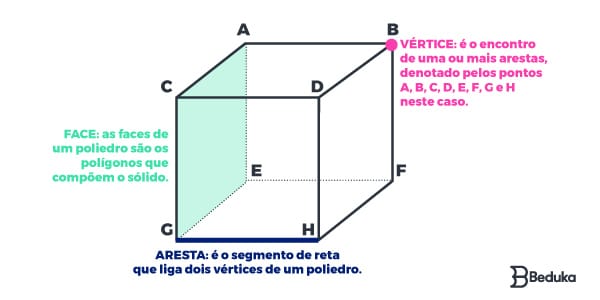
Como já foi dito, os sólidos geométricos são aqueles que possuem três dimensões. Além disso, devem ter pelo menos um dos três elementos seguintes: vértice, aresta e face.
Eles também podem ser classificados em tipos:
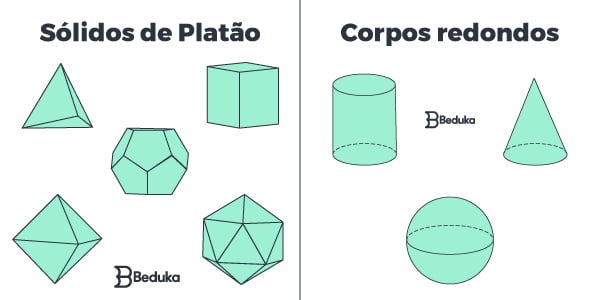
- Poliedros: são fechados e constituídos de faces poligonais, além de ter os 3 elementos (vértice, aresta e face). Exemplos: cubos, paralelepípedos, prismas, pirâmides, etc.
- Corpos redondos: também conhecidos como sólidos de revolução, possuem esse nome porque são criados ao tomar um plano e girá-lo, vendo qual figura forma em movimento. São aqueles que apresentam curvas e a sua medida específica é o raio (r). Exemplos: cilindro, cone, esfera (rotação do círculo), etc.
- Sólidos de Platão: são casos particulares de poliedros regulares, convexos, e congruentes que Platão teorizou e relacionou com os elementos da natureza. Os 5 sólidos clássicos são: tetraedro (pirâmide), hexaedro (cubo), octaedro (8 faces), dodecaedro (12 faces) e icosaedro (20 lados).
O que é Relação de Euler?
Um matemático chamado Euler percebeu que no poliedro havia uma relação constante entre o número de vértices (V), faces (F) e arestas (A).
A fórmula que descreve esse padrão é chamada de relação de Euler, e é dada pela expressão:
V – A + F = 2
Com essa relação é possível descobrir a quantidade de arestas que qualquer poliedro possui, se tivermos o número de faces e de vértices.
Exemplo
1) Maria disse que montaria a maquete de um poliedro com 20 lados, e para isso separou 30 palitos para servir de arestas. Ela ainda pegou 10 bolinhas de isopor para formar os vértices. Será possível montar este poliedro? Se não, quantas bolinhas de isopor faltariam?
Solução:
Primeiro, precisamos conferir se as quantidades que Maria reservou são suficientes para montar o poliedro. Faremos isso utilizando a relação de Euler:
V – A + F = 2
10 – 30 + 20 = 2
0 = 2 (???)
Portanto, concluímos que Maria não conseguiria montar um poliedro com esses materiais.
Agora, a questão pede qual é o número de vértices a mais para que ela conseguisse:
V – A + F = 2
V – 30 + 20 = 2
V = 2 + 30 – 20
V = 12
Dessa forma, será necessário que Maria arranje 2 bolinhas a mais, pois com 12 vértices a relação se verifica verdadeira!
Para que serve o estudo da Geometria Espacial?
Agora que você já entendeu do que se trata, deve ficar pensando qual é o sentido de fazer contas com esses elementos!
O estudo da Geometria Espacial serve como base do nosso dia a dia. Ele compreende as primeiras noções de espaço e tamanho.
Algumas situações em que é preciso ter a visão espacial, são:
Quando um engenheiro constrói um prédio, um arquiteto o esquematiza, ou até quando compramos uma bomba para encher a piscina.
Além disso, na matemática da escola e nas provas, ela serve para lidar com fórmulas e cálculos das dimensões dos sólidos: área e volume. É um assunto que costuma “cair” bastante!
- Vamos aprender como fazer esses cálculos:
Como calcular área total e volume dos sólidos?
Na Geometria Plana, o cálculo do preenchimento da figura era a área, enquanto o do contorno era o perímetro.
Na Geometria Espacial, nós também calculamos. A diferença é que, por ter mais dimensões, o preenchimento será o espaço ocupado internamente (volume) e os contornos serão as áreas das faces (área total).
Cubo: volume e área total
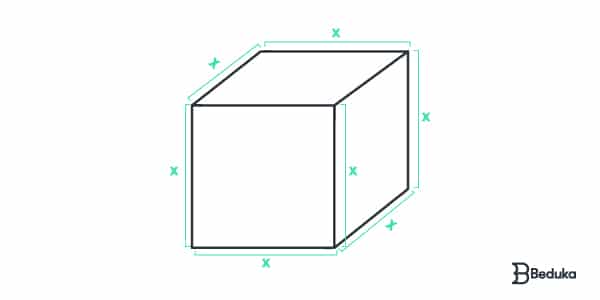
O cubo possui 6 faces de áreas iguais, portanto, a sua área total pode ser dada simplesmente por:
At = 6 . (lado)²
O volume do cubo é dado multiplicando os valores das três dimensões. Como o cubo é formado por arestas de medidas iguais, podemos calcular seu volume simplesmente como:
V = (aresta)³
Paralelepípedo volume e área total
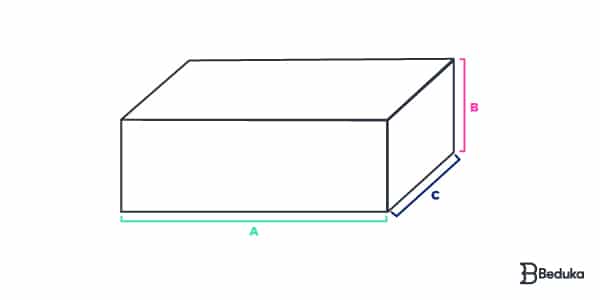
Se um paralelepípedo possui dimensões a, b, c; então:
At = 2ab + 2ac + 2bc
V = a . b . c
Prisma e Pirâmide: volume e área total
O volume e a área total do prisma e da pirâmide dependem do polígono que está na base.
Por isso usamos siglas para escrever a fórmula geral e é tão importante ter aprendido a geometria plana antes.
Antes demostrar as fórmulas, vamos fazer o combinado:
- Ab = área da base: pode ser um triângulo, quadrado, hexágono, etc.
- Al = área lateral: são retângulos nos prismas e triângulos nas pirâmides.
Exemplo: Prisma de base triangular (pbt)
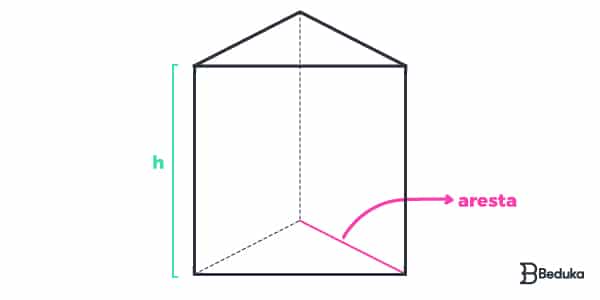
At (pbt) = 2Ab + Al
V (pbt) = Ab . h
(se as 2 bases são um triângulo, logo, ab será a área dos 2 triângulos!)
Exemplo: Pirâmide de base quadrada (pbq)
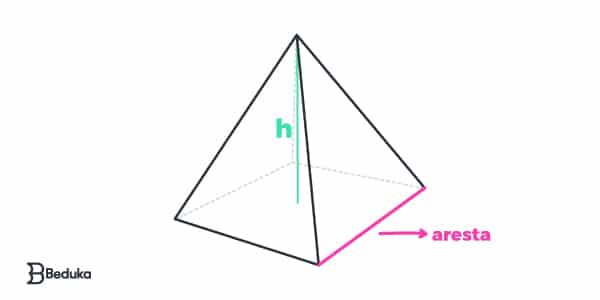
At (pbt) = Ab + Al
(se a base é um quadrado, ab será a fórmula da área do quadrado)
V (pbt) = ⅓ Ab . h
(diferente dos primas, a pirâmide sofre um afunilamento no volume, por isso, contabilizamos apenas ⅓ da área da base).
Cilindro: volume e área total
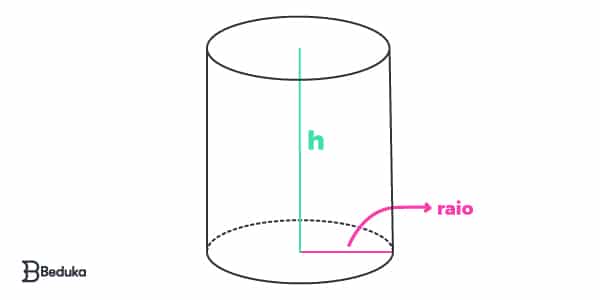
As medidas de corpos redondos são dadas pelo raio (r) e altura (h). Portanto, o cilindro será:
At = 2. π. r . (r + h)
V = π .r . 2 . h
Cone: volume e área total
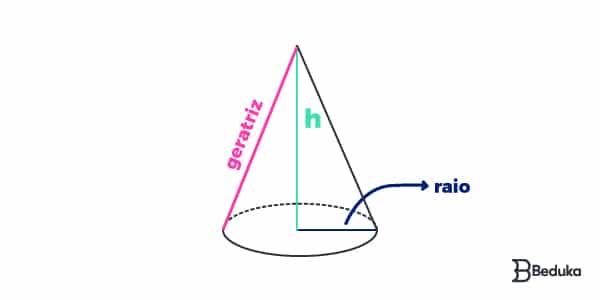
Para calcular a medida da área do cone precisamos, antes, descobrir a geratriz (g). Esse é o segmento que inicia na extremidade do vértice, percorre a superfície do cone e termina em um vértice da circunferência.
Para calcular a geratriz em um cone reto, basta utilizar trigonometria ou o teorema de pitágoras!
Depois, aplicamos os valor nas fórmulas do Cone:
At = π.r.(g + r)
V= 1/3 h.π.r²
Esfera: volume e área total
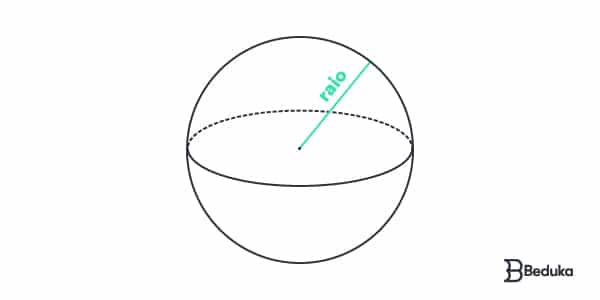
Esse é o mais diferente de todos pois não possui faces com planos definidos!
At = 4 . π . r²
V = 4 ⁄ 3. π . r³
Gostou do nosso artigo sobre Geometria Espacial? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





