Você já ouviu falar nas representações gráficas que são formadas por infinitos pontos, não fazem curva e são unidimensionais (só tem comprimento)? Essas são as retas! Dependendo das características, elas podem ser classificadas em concorrentes, paralelas, transversais, etc. Neste resumo sobre Retas, aprenda os seus tipos, derivações e fórmulas!
Neste resumo sobre retas, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:
- Introdução à Geometria.
- Resumo: O que são retas?
- Principais características das retas.
- Diferença entre reta, semirreta e segmento de reta.
- Quais são os 8 tipos de retas?
- As fórmulas das retas (equação geral e reduzida).
Depois você pode testar o que aprendeu, é só fazer o nosso Simulado ENEM gratuito! Ele pode ser personalizado com as matérias que você quiser.
Introdução: o que é a Geometria?
Antes de tudo, é preciso saber que a reta é um elemento da Geometria. Isso significa que estamos lidando com as representações gráficas (desenhos) da matemática.
O conceito de reta surge na Geometria Plana como consequência do conceito de ponto (literalmente um ponto em qualquer lugar, que marca uma posição identificada por letra maiúscula).
Os elementos citados acima são a base de tudo e logo explicaremos a relação entre eles!
As derivações da ideia de reta, como o segmento de reta, também estão presentes na Geometria Espacial. Fique tranquilo, pois nos próximos tópicos explicaremos os conceitos e daremos exemplos!
Por fim, as retas são muito usadas na Geometria Analítica, uma área que relaciona os desenhos com álgebra.
Nós só estamos querendo te mostrar que esse é um elemento muito básico e importante. Agora, vamos aprender e aprofundar nesses assuntos:
Resumo: O que são retas?
Na Geometria, as retas são definidas como o conjunto de pontos em sequência. Isso significa que elas são como um traço que não faz curva, então não podem ser chamadas de linha.
Já que todo o espaço possui inúmeros pontos possíveis, concluímos que as retas são ilimitadas. Assim, elas não tem começo nem fim. São infinitas!
Compreendido isso, podemos afirmar que as retas são unidimensionais. Em outras palavras, só podemos medir o seu comprimento e não conseguimos encontrar valores para profundidade ou altura.
O jeito mais comum de representar as retas por escrito é colocar um traço (com setas nas duas pontas) acima do nome de dois pontos que passam pela reta. Isso é para representar sua infinitude.
Além disso, o nome de cada reta é dado por letras minúsculas.
Note que é preciso ter, no mínimo, dois pontos para formar uma reta. Além disso, a reta que passa por esses dois pontos (A e B) é uma reta específica (a reta r). A reta que passa pelos pontos A e D, por exemplo, é outra.
Com isso, concluímos que por um ponto qualquer e sozinho, podem passar infinitas retas. Porém, quando determinamos os demais pontos, estamos identificando uma reta específica.
Dependendo de onde esses pontos estão alinhados, as retas podem estar em 3 posições diferentes: horizontal, vertical ou inclinada.
Resumo das principais características das retas
Essas características já foram explicadas nas frases em negrito anteriormente, mas fizemos um resumo em tópicos para te ajudar a memorizar:
- São infinitas;
- São unidimensionais;
- Não fazem curva;
- São representadas por letras minúsculas;
- Podem estar nas posições verticais, horizontais ou inclinadas;
- É preciso, no mínimo, dois pontos para se formar uma reta.
Aprenda como fazer resumos para te ajudar a rever cada matéria!
Diferença entre reta, semirreta e segmento de reta
Você já entendeu que a reta é infinita e é o alinhamento de pontos. Mas já imaginou o que fazer se eu quero analisar um pedaço específico dela?
Por isso, há os conceitos que se derivam da reta, chamados de segmentos de reta e semirreta.
Entenda as suas características:
O que são Semirretas?
As semirretas são encontradas dentro de uma reta, pois elas começam em um ponto pertencente à reta e analisamos tudo o que vem depois. Em outras palavras, elas têm início e não tem fim! É como se, em algum ponto, a reta sofresse um corte.
O jeito de representá-las é colocar um traço (com uma seta na ponta direita), acima das letras que representam dois pontos por onde passa. O primeiro ponto tem que ser onde a semirreta começa, o segundo é para indicar a direção que percorrerá.
- São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
O que são Segmentos de Reta?
O segmento de reta é definido como uma parte da reta que pode ser medida. Isso significa que pegamos a reta e delimitamos um segmento finito dentro dela. Por isso, o segmento de reta tem início e tem fim.
Outra definição para isso é: “a menor distância entre dois pontos”. Então, são esses segmentos que formam os lados e arestas das figuras geométricas!
O jeito de representá-los é colocar um traço (sem seta em nenhuma ponta), acima das letras que representam os dois pontos que o limitam. O primeiro ponto tem que ser onde o segmento começa, o segundo é onde ele termina
Quais são os tipos de retas que existem?
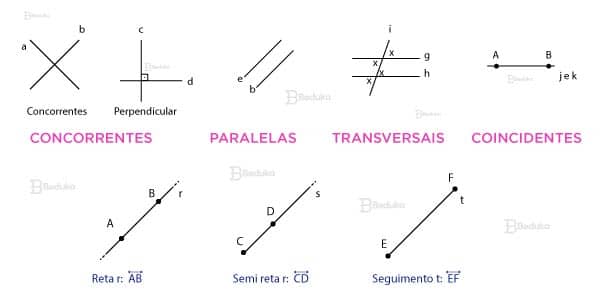
Durante os exercícios, você pode se deparar com nomes assim: “retas concorrentes” ou “retas paralelas”. Saber o que isso significa, como representar e suas consequências são essenciais para resolver bem a questão!
Se você não entendeu nada, fique tranquilo porque vamos te explicar cada um dos 8 tipos que existem.
Mesmo que você já saiba o que significam esses dois nomes acima, sugerimos que dê uma olhada nos outros seis! Só pra se certificar…
O que são retas Concorrentes (Perpendiculares e Oblíquas)?
Podemos afirmar que duas retas são concorrentes quando elas se cruzam em apenas um ponto comum. Como consequência, haverá a formação de um ângulo.
Quando o ângulo formado entre as duas retas for de exatamente 90° graus, também conhecido como ângulo reto), elas receberão o nome de Perpendicular.
As retas oblíquas são aquelas que são concorrentes, mas não são perpendiculares. Sendo assim, são livres para formar qualquer tipo de ângulo que não seja o de 90°.
O que são retas Paralelas?
Duas (ou mais) retas são chamadas de paralelas quando não existe nenhum ponto comum entre elas. Assim, elas não se cruzam e não formam nenhum ângulo. Estão perfeitamente alinhadas, lado a lado.
Se duas retas estiverem representadas com as partes visíveis não se cruzando, lembre-se de prolongar as retas para conferir. Se a prolongação delas se cruzar, então não será paralela, porque é infinita e uma hora se encontrará.
Essa é uma pegadinha que sempre cai! Mas só costuma acontecer quando as retas estão em inclinações diferentes.
O símbolo usado para representar duas retas paralelas são as barras duplas. Assim, se queremos dizer que as retas c e b são paralelas, escreveremos: c // b .
O que são retas Coincidentes?
Retas coincidentes são aquelas que possuem, no mínimo, dois pontos em comum. Como consequência, os demais também estarão.
Assim, podemos dizer que elas estão sobrepostas, ou seja, possuem todos os pontos em comum. Neste caso, o efeito que dá é vermos que elas ocupam o mesmo lugar, como se fossem uma reta só.
O que são retas Transversais?
As retas são chamadas de transversais quando analisamos duas paralelas cortadas por uma terceira e mesma reta oblíqua! A imagem que fica é como a do símbolo de “diferente”, assim: ≠.
Esse tipo de posição entre retas é muito importante porque cria uma relação de congruência entre os diversos ângulos formados.
O que são retas Coplanares?
Retas coplanares são aquelas que estão presentes no mesmo plano de um espaço, ou seja, no mesmo universo geométrico.
O que são retas Reversas?
Retas reversas são aquelas que estão em diferentes planos do espaço, cada uma sendo analisada em uma situação e local diferentes
Quais são as fórmulas das retas?
Se, na sua trajetória escolar, você ainda não viu as funções matemáticas, com certeza passará pelo assunto! Principalmente se tratando das funções de primeiro grau, que são as mais básicas!
Não por coincidência, o gráfico dessa função tem o formato de uma reta. E adivinha só? É porque a lei de formação de uma função de 1° grau segue o mesmo modelo que a equação reduzida da reta!
Não entendeu nada? Calma, vamos te explicar:
Qual é a Equação Geral da Reta?
Quando desenhamos uma reta no plano cartesiano, podemos escrever um cálculo que representa aquela reta, sua posição e inclinação.
Como as retas possuem a mesma característica, a estrutura dessa fórmula será a mesma para todas as retas. O que muda são os números que se referem às características próprias que diferenciam a reta “r” da “s”.
Assim, se soubermos a equação geral das retas, poderemos encontrar qualquer uma delas trocando apenas alguns elementos. Veja:
ax + by + c = 0
Nesta fórmula, os números dos pontos que a compõem são colocados no lugar de “x” e “y”, referindo às coordenadas. “a”, “b” e “c” são coeficientes que determinam outras características, como inclinação.
Na realidade, nós temos o costume de usar mais a fórmula reduzida, que é um resumo desta. Vamos vê-la:
Qual é a Equação Reduzida da Reta?
A equação reduzida da reta é dada por:
y = mx + n
Para encontrar a equação reduzida de uma reta, é necessário descobrir os valores do coeficientes m e n e montar a equação final!
Há ainda a possibilidade de encontrar o valor do coeficiente angular e conhecer um ponto. Só é preciso duas informações para encontrar o resto!
O coeficiente linear (n) é simples: basta saber que ele é o valor da ordenada (y) quando x = 0. Isso significa que n é onde a reta corta o eixo y, o ponto (0,n).
Para calcular o coeficiente angular (m) da reta, existem duas possibilidades:
- Saber que ele é igual à tangente do ângulo α:
m = tg α
- Usar a fórmula quando se tem dois pontos coordenados da reta:
Seja A(x1,y1) e B (x2,y2), então o coeficiente angular pode ser calculado por:
m = y2 – y1 / x2 – x1
Para tomar a decisão sobre qual método utilizar para calcular o coeficiente angular da reta, é necessário analisar quais são as informações que temos.
- Esse assunto pertence à Geometria Analítica, na qual você ainda pode descobrir outras fórmulas e possibilidades de relacionar retas com pontos e matrizes!
Gostou do nosso resumo de retas? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





