As funções matemáticas são regras que relacionam dois valores dependentes (x e y). Isso significa que para cada valor colocado em x, será gerado um valor em y. Os possíveis números em x e y são agrupados em conjuntos, respectivamente chamados de domínio e contradomínio. Existem algumas propriedades e certos gráficos para cada tipo de função!
Neste artigo sobre Funções Matemáticas, você encontrará:
- O que são funções: definição, exemplos e para quê serve.
- Elementos da Função: Domínio, Contradomínio e Imagem.
- Quais são os tipos de função?
- Bijetora, Sobrejetora, Injetora.
- Constante.
- De 1° Grau.
- De 2° Grau.
- Exponencial.
- Logarítmica.
- Par e ímpar.
- Crescente e decrescente.
- Trigonométrica.
- Como calcular e resolver uma função.
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que são Funções Matemáticas
As funções matemáticas são expressões numéricas e algébricas (números e letras) que possuem dois lados separados pelo sinal de igual (=) e obedecem uma regra, a lei de formação.
De um lado temos o “f(x)” que representa o valor final da função. Esse valor também pode ser representado por “y”. Do outro lado, temos a regra matemática, ou seja, um conjunto de números que rodeiam o valor “x”.
Todos os valores que desconhecemos são chamados de incógnitas e são representados por letras.
Quando usamos a expressão “em função de” gera uma ideia de relação entre as coisas. Portanto, ser uma função significa ter dependência, ou seja, o valor da função “f(x)” ou “y” se modifica à medida que modificamos o valor de “x”.
Por isso, devemos resolver as funções pensando nos pares ordenados (x , y) que se adequam àquela regra. A regra define a “cara” de cada função: como será o seu gráfico e qual a proporção que há entre x e y (se um será o dobro do outro, ou o triplo, ou outra razão).
Exemplo:

Para quê servem as Funções Matemáticas
As Funções servem para nos auxiliar a resolver problemas em que há muitas possibilidades. Elas nos apontam quais são os limites aceitáveis dentre as opções e também servem para formar previsões e estimar o resultado de um fenômeno.
- Portanto, o objetivo de se resolver uma função é descobrir os valores de interesse, de acordo com cada contexto dado.
Exemplo de 2 situações que se resolve com funções:
- Um biólogo observou que há uma população inicial de x bactérias hoje, e deseja saber qual será a quantidade daqui a 10 anos se elas continuarem se reproduzindo num determinado ritmo.
- Um padeiro produz uma quantidade de pães e quer dar descontos a cada grande quantidade vendida. Ele precisa calcular até que ponto esse desconto é vantajoso, pois pode não ser bom para o cliente ou levá-lo a ter prejuízo.
Elementos da função: Domínio, Contradomínio e Imagem
Para entender melhor, precisamos conhecer os componentes das funções. Veja:
- Os valores que podemos colocar em “x” são agrupados em um conjunto chamado Domínio (D).
- Todos os valores possíveis de serem gerados a partir disso são chamados de Contradomínio (CD).
- Mas, aqueles do CD que satisfazem a função (o y de cada x) pertencem ao conjunto chamado Imagem (I).
Observe o desenho abaixo para entender melhor:
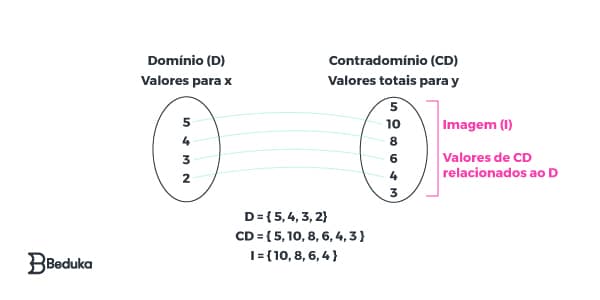
Existem duas condições para a relação entre conjuntos ser considerada função:
- O domínio deve ser exatamente igual ao conjunto de partida, ou seja, todo elemento de (D) é ponto de partida “das flechas”, os possíveis valores de “x”. Se houver um elemento de D que não “parta uma flecha”, não é uma função!
- Cada elemento de D só pode ter uma correspondência no conjunto CD. De forma figurada, só pode “partir 1 flecha” de cada elemento do Domínio. Se um valor em D tiver “duas flechas” saindo de si mesmo, não é uma função!
Quais são as Funções Matemáticas?
As funções podem ser classificadas de diversas formas:
- Quanto aos conjuntos (Injetora, Sobrejetora e Bijetora)
- Quanto ao desenho do gráfico (Crescente, Decrescente, Constante, Afim)
- Quanto à lei que a descreve (1° grau, 2° grau, Exponencial, Logarítmica, etc.)
Algumas funções podem ser de dois tipos ao mesmo tempo, ou seja, se completam como nome e sobrenome. Também existem outras que nunca podem ser 2 ao mesmo tempo.
Exemplo:
Funções de Primeiro Grau podem ser decrescentes e outras que são crescentes. Mas nunca existirá uma função exponencial que seja constante, pois uma lei de formação anula a outra.
Complexo não é? Por isso, vamos estudar cada tipo e suas características:
Função Injetora, Sobrejetora e Bijetora
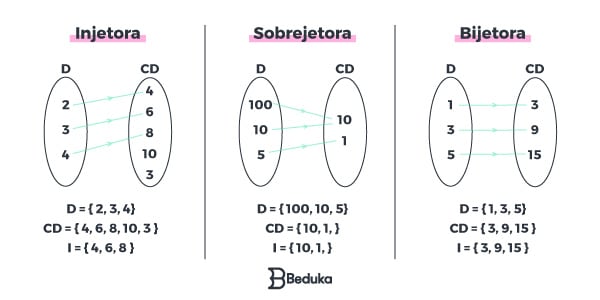
- Função Injetora
Cada elemento do Domínio possui um único elemento na Imagem e vice-versa. Porém, podem existir elementos do Contradomínio que não são Imagem, eles sobram no conjunto. Portanto, a Imagem é diferente do Contradomínio.
- Função Sobrejetora
Nesta função, cada elemento do Domínio possui um elemento na Imagem, mas pode acontecer de dois elementos do Domínio possuírem uma mesma imagem. O que não pode é um elemento do D possuir 2 imagens. Dessa forma, Imagem e o Contradomínio são iguais, não há sobra.
- Função Bijetora
Cada elemento do Domínio possui um único elemento na Imagem e vice-versa, só que não há elementos que sobram. Por isso, ela pega um aspecto da Injetora (um elemento da Imagem só pertence a um elemento do Domínio) e outro aspecto da Sobrejetora (não sobram elementos, imagem é igual ao contradomínio).
Função Constante
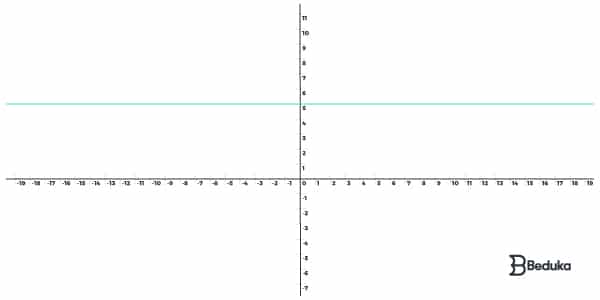
Na função Constante, qualquer número que colocar em x sempre resultará no mesmo valor de Y. Por esse motivo, o gráfico (resultados possíveis de cada par ordenado) é uma linha horizontal e reta.
Função de Primeiro Grau
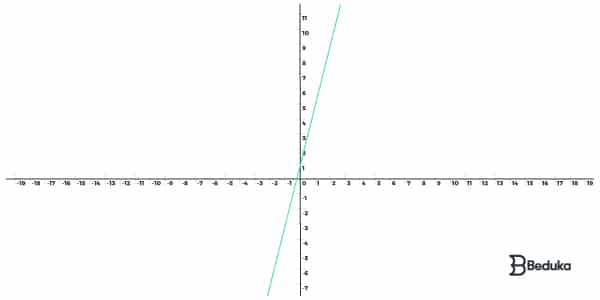
Uma função do primeiro grau é aquela em que a lei de formação pode ser escrita na seguinte maneira:
f(x) = ax + b
Além disso, o expoente que há na incógnita vale no máximo 1. Por isso é chamada de primeiro grau! Como consequência disso, seu gráfico é sempre uma reta.
As funções de primeiro grau podem ser chamadas de Afim e apresentam alguns tipos: Identidade ou Linear.
- Confira o artigo completo da função afim para se aprofundar nos cálculos, nos componentes da sua lei e veja exercícios resolvidos!
Função de Segundo Grau – Quadrática
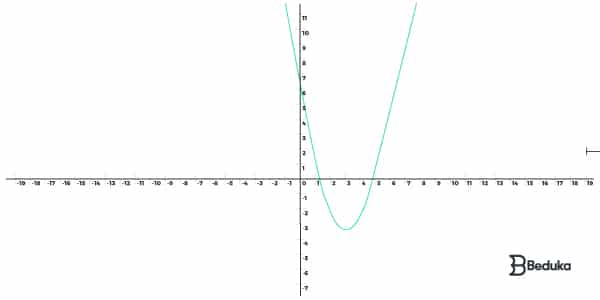
Uma função do segundo grau é aquela em que a lei de formação pode ser escrita na seguinte maneira:
f(x) = ax² + bx + c
Além disso, deve haver ao menos um expoente máximo valendo 2, na incógnita . Por isso é chamada de segundo grau! Como consequência disso, seu gráfico é sempre uma parábola.
Observe que o gráfico é composto por um segmento com duas características: uma crescente e outra decrescente. Observe também que ela pode ou não ser simétrica. Se for, pode ser do tipo par ou ímpar!
- Confira o artigo completo da função de segundo grau para se aprofundar nos cálculos, nos componentes da sua lei e na Fórmula de Bháskara!
Função Exponencial
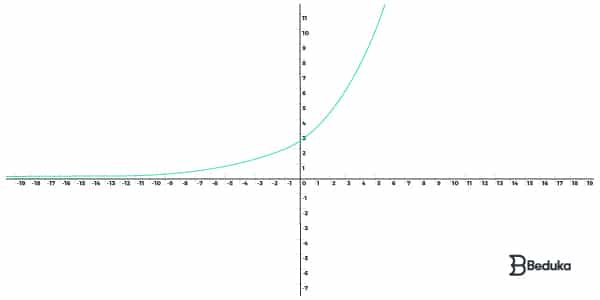
Uma Função Exponencial é caracterizada pela presença da variável (x) no expoente de uma base numérica, em que a lei de formação pode ser escrita na seguinte maneira:
f(x) = aˣ
Por esse motivo, o seu gráfico é como um braço de hipérbole.
- Confira o artigo completo da função exponencial para se aprofundar nos cálculos, nos componentes da sua lei e ver exercícios resolvidos!
Função Logarítmica
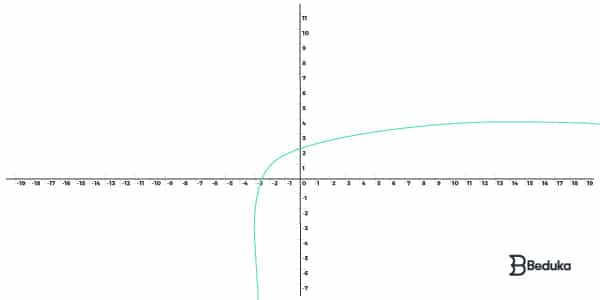
É toda função que possuir um logaritmo na sua lei de formação, seguindo as condições de existência:
f(x) = loga x
O Log é tido como operação inversa da exponenciação, da mesma forma, os gráficos também são inversos.
- Confira o artigo completo sobre funções logarítmicas para saber como resolver!
Função Par
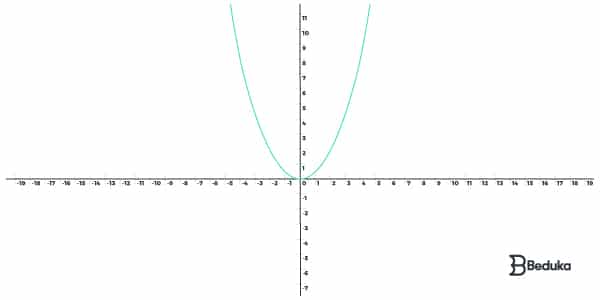
A função par é toda aquela que for simétrica em relação ao eixo vertical (y) do plano cartesiano. Ao analisar a linha que se forma interligando os possíveis resultados, vemos que elas são como um reflexo de um espelho.
Função Ímpar
A função ímpar é toda aquela que for simétrica em relação ao eixo horizontal (x) do plano cartesiano. Imagine que é uma folha de papel e você dobra bem no lugar do eixo indicado. Observe que as figuras de cada face se encontrarão!
Função Crescente e Decrescente
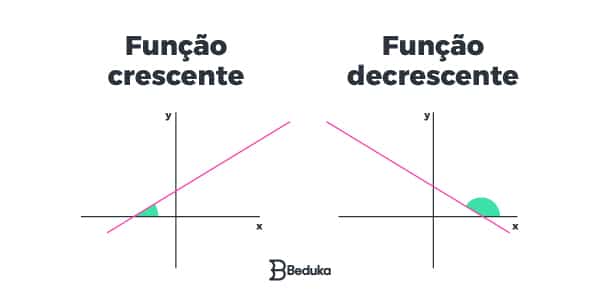
- Crescente: Função que ao aumentar o valor de x, gera um valor maior de y.
- Decrescente: Função que ao aumentar o valor de x, reduz o valor de y.
As funções de 1° grau, exponenciais e logarítmicas podem ser de um tipo ou de outro. Já as funções de 2° grau e trigonométricas, apresentam um gráfico que contém segmentos dos dois tipos ao mesmo tempo!
Função Trigonométrica
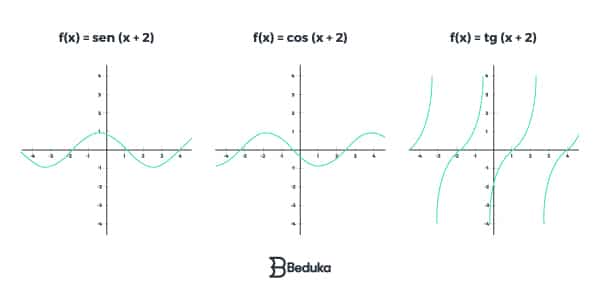
São funções angulares utilizadas no estudo dos triângulos ou fenômenos periódicos. Sua lei de formação sempre terá algum fator trigonométrico:
f(x) = sen x
f(x) = cos x
f(x) = tg x
Seu gráfico depende de qual dos 3 fenômenos se associa!
- Temos um artigo explicando tudo sobre as Funções trigonométricas!
Como calcular uma função – Resolvendo as funções matemáticas!
Para resolver qualquer função, basta saber a sua lei de formação, substituir os valores dados e encontrar os que faltam. Depois, resolvemos as funções como se fossem equações.
O passo a passo básico de toda resolução é:
- 1.Substituir valores dados
Saiba identificar o que cada incógnita representa na conta, leia o enunciado e substitui na lei de formação. Agora, você só terá que pôr a mão na massa e resolver as contas, seguindo as dicas:
- 2.Eliminar os parênteses fazendo as operações prioritárias
Algumas expressões podem estar escritas dentro de símbolos, como os parênteses ( ) , os colchetes [ ] e as chaves { }. Eles indicam a ordem: 1° resolvemos o que está dentro dos parênteses, 2° o que está dentro dos colchetes e 3° o que está dentro das chaves.
Se for impossível continuar resolvendo o que está em 1° lugar de prioridade, pulamos para o próximo passo. Apenas depois disso podemos resolver o que está fora.
Uma vez que identificamos as prioridades, podemos efetuar as operações. Elas também têm uma ordem: 1º potenciação e radiciação; 2º multiplicação e divisão e 3º soma e subtração.
Se existir mais de uma operação com a mesma prioridade, elas serão resolvidas da esquerda para direita.
- 3. Efetuar a transposição de termos
Após isso, para podermos trocar os termos e organizá-los em cada membro, devemos mudar o sinal que ele carregava para o seu oposto:
Aquilo que está negativo passa como positivo e vice-versa
O que está multiplicando passa dividindo e vice-versa
Se havia raiz quadrada, passa como potência de expoente ½ e vice-versa
Ao passar as incógnitas de lado, devemos mantê-las juntas aos seus coeficientes e à base em que está.
- 4. Reduzir os termos semelhantes
Depois disso, efetuamos as operações entre os termos semelhantes (número com número, letra com letra).
- 5. Isolar a incógnita e encontrar seu valor numérico
Quando não há mais nada a ser feito, aí isolamos a incógnita de um lado e aplicamos as propriedades ou operações para descobrir seu valor.
ATENÇÃO!!!
O que vai diferenciar na resolução de uma função para outra será as condições de existência de cada uma e quais os recursos matemáticos que utilizaremos para prosseguir com as contas.
Exemplo:
Quando nos depararmos com uma função exponencial, chegará um momento em que precisaremos do conhecimento da potenciação. Já nas funções logarítmicas, precisaremos das propriedades do logaritmo.
- Agora cabe a você estudar cada link que colocamos para se aprofundar nas propriedades de cada função.
Gostou do nosso artigo sobre Funções Matemáticas? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





