Resumo de Conjuntos Numéricos: de maneira simples e completa!

Essa é uma daquelas matérias que dá arrepios só de lembrar. Aprendemos tudo na decoreba, e o pior: seus símbolos nos acompanham por toda a vida escolar… Mas é hora de acabar com esse pesadelo. Que tal aprender tudo sobre os Conjuntos numéricos? Neste resumo, você vai entender o que são eles e como usá-los!

Neste resumo, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:

1. Resumo sobre o que são conjuntos numéricos?
2. Quais são os conjuntos numéricos?
3. Resumo do Conjunto dos Números Naturais (N)
4. Resumo do Conjunto dos Números Inteiros (Z)
5. Resumo do Conjunto dos Números Racionais (Q)
6. Resumo do Conjunto dos Números Irracionais (I)
7. Resumo do Conjunto dos Números Reais (R)
8. Gráfico da relação entre os Conjuntos Numéricos!

Organize seu tempo de estudos com o Plano de Estudos Beduka! Com ele você conseguirá encaixar uma rotina eficaz de estudos junto aos demais afazeres do dia. 

O que são Conjuntos Numéricos?

Bem, você deve estar cansado de saber que um Conjunto é o agrupamento de elementos, normalmente com as mesmas características. Quando esses elementos são números, então nós teremos um conjunto numérico! 

É bem claro que a matemática tem uma infinidade de números. A gente vai crescendo e aprendendo sobre frações, dízimas, números negativos, decimais… 

Eles são infinitos, mas cada tipo é mais fácil de ser usado em determinada situação, por causa de suas propriedades.

Por isso, nós aprendemos a agrupar os números, o que deu origem à matéria chamada de Teoria dos Conjuntos. Cada tipo de conjunto é representado por uma letra maiúscula.

• São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

Quais são os Conjuntos Numéricos?

Existem várias formas de agrupar os números em conjuntos. Tudo depende de qual característica observamos como a regra daquele grupo. 

Porém, alguns desses conjuntos são mais presentes na vida do estudante, por conta da frequência com que aparecem nas soluções matemáticas (e nas suas provas). 

São eles: 

• Conjuntos dos números Naturais;
• Conjuntos dos números Inteiros;
• Conjuntos dos números Racionais;
• Conjuntos dos números Irracionais;
• Conjuntos dos números Reais.

Calma! É mais simples do que parece. 

Agora nós vamos entender o que é cada um deles, ver exemplos e definições bem simples. Se você prestar bastante atenção, sairá sabendo a matéria num piscar de olhos. Nem vai doer! 

Vamos lá:

Conjunto dos Números Naturais (N)

O Conjunto dos Números Naturais é um grupo de números representados pela letra N. 

Esse foi o primeiro conjunto numérico que surgiu, quando as pessoas estavam fazendo contagens e precisavam dar símbolos que remetiam a valores. 

Por isso, ele é o mais simples e seus números seguem duas características ao mesmo tempo:

• São números inteiros (não tem parte decimal ou vírgula);
• São números positivos (contamos de 0 para cima, ou seja, N > 0).

Lembre-se: o símbolo “>” significa “maior que”.

Agora você entendeu: é por isso que usamos o “n” (minúsculo) para nos referir a um número qualquer. Já nas matérias mais avançadas de álgebra, nós chamaremos ele de “x”.

Exemplo de conjunto de números naturais

Portanto, o conjunto dos números naturais (N) possui os seguintes elementos:

N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …}

Importante: as chaves { } são usadas antes do primeiro número e ao final, para dar ideia de um grupo fechado. Os pontos de reticência dão a ideia de infinidade, já que podemos contar até o infinito!

Até aqui tudo bem né? A esta altura do resumo de conjuntos numéricos nós Já entendemos que o Conjunto dos Números Naturais inicia-se no zero e é infinito! Agora vamos entender mais uma coisinha:

Subconjuntos dos Números Naturais

Os subconjuntos são pequenos conjuntos que podemos formar dentro de um conjunto. 

Que confuso… Vamos entender com algo mais prático:

Você vai ao mercado e se depara com várias coisas de diferentes tipos. Mas o mercado está separado em seções: “hortifruti”, “alimentos não perecíveis”, “equipamento de limpeza”.

Então o “hortifruti” é um conjunto de elementos do mercado, caracterizado por elementos que são frutas. 

Porém, nós podemos pegar esse conjunto de frutas e criar mini-conjuntos dentro dele, separando mais ainda: frutas cítricas e as frutas doces. Aí está: dois subconjuntos!

Retomando: o mesmo acontece com os conjuntos numéricos. Para indicar subconjuntos de um determinado conjunto, nós usamos símbolos.

Fica assim:

• N* = subconjunto dos números naturais que está sem o zero. Então, seria N* = {1, 2, 3, 4, 5, …, n, …}. Outra forma de representar é com uma operação: N* = N – {0}.
• Np = conjunto dos números naturais pares. Np = {0, 2, 4, 6, 8…, 2n, …}.
• Ni = conjunto dos números naturais ímpares. Ni = {1, 3, 5, 7, 9…, 2n+1, …}. 
• P = conjunto dos números naturais primos. P = {2, 3, 5, 7, 11, 13, …}.

Conjunto dos Números Inteiros (Z)

O Conjunto dos Números Inteiros é representado pela letra Z.

Ele é como uma extensão do conjunto dos números naturais, ou seja, tem todos os números do N, porém adiciona alguns exclusivos dele. É isso que o torna diferente.

Sendo assim, ele é constituído pela união (U) dos elementos do conjunto dos números naturais com os números negativos. 

Exemplo de conjunto de números inteiros

Simples né? Podemos dizer que o conjunto dos números inteiros, possui os seguintes elementos:

Z = {…, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, …}

Subconjuntos dos Números Inteiros

Ele também possui alguns subconjuntos representados por símbolos:

• Z* = conjuntos dos números inteiros não-nulos, ou seja, sem o zero. Z* = {…, –4, –3, –2, –1, 1, 2, 3, 4, …} ou Z* = Z – {0}.
• Z+ = conjunto dos números inteiros e positivos (não-negativos). Z+ = {0, 1, 2, 3, 4, 5, …}. Sim, ele possui os mesmos elementos que o N. Então podemos dizer que Z+ = N.
• Z*+ = conjunto dos números inteiros positivos e sem o zero. Z*+ = {1, 2, 3, 4, 5, …}.
• Z – = conjunto dos números inteiros negativos (não-positivos). Z- = {…, –5, –4, –3, –2, –1, 0}.
• Z*– = conjunto dos números inteiros negativos e sem o zero. Z*- = {…, –5, –4, –3, –2, –1}.

Esse resumo de conjuntos numéricos está um pouquinho grande, mas já estamos chegando ao final. Vamos lá!

Conjunto dos Números Racionais (Q)

O Conjunto dos Números Racionais é representado pela letra Q.

O raciocínio aqui é o mesmo: ele tem todos os elementos dos conjuntos anteriores (N e Z), somados a alguns exclusivos, que o diferencia. Neste caso, estamos incluindo os números não-inteiros, ou seja, os que são decimais e as frações.

Exemplo de conjunto de números racionais

O conjunto dos números racionais possui os seguintes elementos:

Q = {x ∈ Q: x = a/b, a ∈ Z e b ∈ N}

Não se desespere! Vamos te explicar o que essas letras significam.

No nosso artigo sobre como funciona o diagrama de Venn, você entende que o símbolo “∈” significa “pertence”, ou seja, “é daquele cojunto”.

Então, a definição acima é lida desta forma: um número qualquer “x” pertence aos racionais quando “x” é igual a “a” dividido por “b”. Isso só é possível se “a” pertencer aos inteiros e “b” pertencer aos naturais.

Em outras palavras, se é fração ou um número que pode ser escrito na forma de fração, então é um número racional.

Os números que podem ser escritos na forma de fração são:

• Todos os números inteiros;
• Decimais finitos;
• Dízimas periódicas.

Os decimais finitos são aqueles que possuem um número finito de casas decimais. Como por exemplo:

• 0,1
• 3,5
• 6,32

Dízimas periódicas são decimais infinitos, mas que repetem a sequência final de suas casas decimais. Por exemplo:

• 5,22222…
• 4,45454545….
• 7,255255255255….

Subconjuntos dos Números Racionais

Já falamos demais! Vamos para a última parte, os subconjuntos:

• Q* = subconjunto dos números racionais não-nulos, formado pelos números racionais sem o zero;
• Q+ = subconjunto dos números racionais não-negativos, formado pelos números racionais positivos e o zero;
• Q*+ = subconjunto dos números racionais positivos, formado pelos números racionais positivos, sem o zero;
• Q– = subconjunto dos números racionais não-positivos, formado pelos números racionais negativos e o zero;
• Q*– = subconjunto dos números racionais negativos, formado números racionais negativos, sem o zero.

Conjunto dos Números Irracionais (I)

O Conjunto dos Números Irracionais é representado pela letra I.

Novamente aplicamos aquele raciocínio de juntar tudo mais alguns elementos novos e exclusivos desse grupo. A sua diferença é que ele possui também todos os outros números que NÃO pertencem ao conjunto dos racionais.

Exemplo de conjunto de números irracionais

Podemos definir também o conjunto dos números irracionais da seguinte forma: Os números irracionais são os que NÃO podem ser escritos na forma de fração. São eles:

• Decimais infinitos;
• Raízes não exatas.

Os decimais infinitos são números que possuem infinitas casas decimais e que não são dízimas periódicas. Tais como:

• 0,1541984561354…
• √2
• π

Ufa! Só temos mais um inimigo para derrotar. Vamos ao último grupo do nosso resumo de conjuntos numéricos:

Conjunto dos Números Reais (R)

O Conjunto dos Números Reais é representado pela letra R.

Ele é o conjunto master, aquele que contém todos os anteriores. Ele é o mais completo e o maior! 

Sendo assim, ele pode ser definido pela união (U) do conjunto dos números racionais e o conjunto dos números irracionais. 

O Conjunto dos Números Reais pode ser escrito matematicamente desta forma:

R = Q U I = {Q + I}

• Nós usamos todos esses sinais, nomes e letras principalmente na hora de dar soluções para as funções de segundo grau!

Gráfico de relações sobre o resumo de conjuntos numéricos!

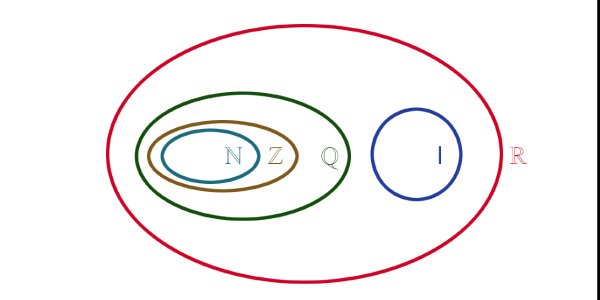
Existe uma forma de representar tudo isso que nós dissemos. Observe a imagem acima com atenção!

A legenda é assim:

• N C Z C Q C R → Lê-se: “N está contido em Z, que está contido em Q e que está contido em R”.
• I C R → “I está contido em R”.
• Q U I = R → “Q união com I, corresponde a R”.
• Q ∩ I = Ø → “Q intersecção com I, corresponde a vazio”.
• I = R – Q → “I corresponde a R, subtraído de Q”.

Agora que já finalizou o resumo, você pode testar os seus conhecimentos com os nossos exercícios sobre conjuntos! 

Além de treinar com eles, você pode fazer o nosso Simulado ENEM gratuito! Personalize com as matérias que você quiser.

Gostou do nosso resumo de Conjuntos Numéricos? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!