O Diagrama de Venn é um desenho gráfico utilizado, principalmente, para estudar os Conjuntos Numéricos. Por meio dele, podemos interpretar e estabelecer relações ou operações. Cada círculo é um conjunto e o modo como estão posicionados indicam a leitura correta!
Neste artigo sobre o Diagrama de Venn, você encontrará:
- O que é Diagrama de Venn e para quê ele serve?
- Como funciona e para que serve
- Exemplos de relação entre conjuntos
- Operações de conjunto com o diagrama
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que é Diagrama de Venn e para quê ele serve?
O Diagrama de Venn é uma representação gráfica, ou seja, um desenho técnico. Ele é mais famoso por ser aplicado na matemática, principalmente na matéria de Conjuntos Numéricos. Ele ainda pode ser chamado de Diagrama de Venn-Euler ou Diagrama de Conjunto.
Contudo, ele também é utilizado na lógica e na identificação de dados sociais ou de mercado. Com ele, é possível calcular a quantidade de pessoas que foram afetadas, por exemplo, por alguma doença. Ainda podemos utilizá-lo para “pesquisas de gostos” na área de vendas.
Para nós, a ideia do diagrama é facilitar o entendimento nas operações básicas de conjuntos, portanto, devemos compreender como interpretá-lo.
Como funciona o Diagrama de Venn
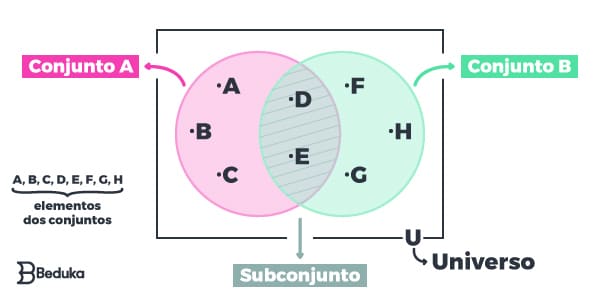
O Diagrama é formado por uma linha fechada sem auto-intersecção, ou seja, por círculos. Eles formam áreas com número dentro si, isto é, cada círculo representa um determinado conjunto. Quando essas circunferências se cruzam, acabam criando os subconjuntos.
Para representar o Universo total de números e possibilidades, põe-se um retângulo delimitando a área que inclui todas as circunferências. Nem sempre esse elemento aparece, pois é mais relevante na resolução de exercícios que citam outros números não pertencentes aos círculos. Assim, descobrimos onde posicioná-los no gráfico.
Relação entre conjuntos – Exemplos com o Diagrama de Venn
De acordo com a imagem do gráfico e interpretando corretamente, podemos observar diferentes relações entre os conjuntos. Vamos compreender os termos matemáticos que utilizamos para diferenciar cada relação:
Conjunto único
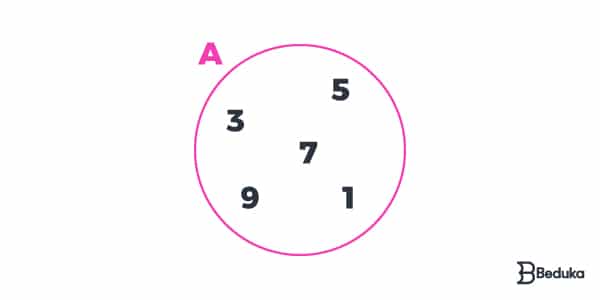
Como o próprio nome aponta, ele se trata de uma circunferência só, é apenas um agrupamento de números.
Supondo que dentro de uma sacola há 5 bolinhas e que cada uma está enumerada com um dos seguintes números: 1, 3, 5, 7 e 9. Assim o meu conjunto é A = {1,3,5,7,9} e sua representação no Diagrama seria a indicada na imagem acima.
Conjuntos Disjuntos

Quando há dois conjuntos, fazemos dois círculos e os posicionamos de acordo com a relação que há entre eles.
Se eu mantenho a primeira sacola A = {10, 13, 16 e 19} e pego outra com bolas diferentes, enumeradas de 1 a 4, formaria o conjunto B = {1, 2, 3 e 4}. Eles não possuem nenhum elemento em comum então são chamados de Disjuntos.
Os Conjuntos Disjuntos não se tocam em nenhum ponto na representação gráfica.
A ideia da utilização para 3 conjuntos ou mais é bem semelhante. A única diferença é que eles podem ser:
Disjuntos um a um: nenhum deles compartilha nada com nenhum outro.
Disjuntos dois a dois: somente dois deles compartilham algum ponto.
Relação de Pertinência ou Pertença (∈)
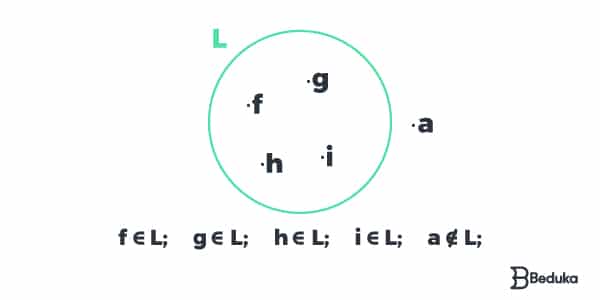
É por meio da observação da relação de Pertinência que descobrimos se um elemento pertence ou não a determinado conjunto. Para isso, utilizamos o símbolo (∈), mas quando ele não pertence, fazemos um traço neste símbolo (∉).
Exemplo:
Considere o conjunto L = {f, g, h, i}. Logo percebemos que “f” pertence mas “a” não. No diagrama, teremos a formação da imagem que está logo abaixo do título deste tópico!
Relação de inclusão (⊂)
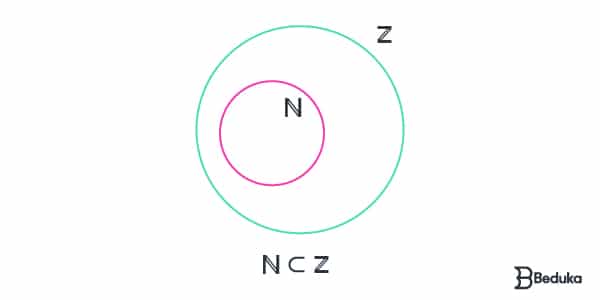
É por meio da observação da relação de Inclusão que descobrimos se um conjunto está contido ou não dentro de outro conjunto. Assim, analisamos os subconjuntos entre si. Para isso, utilizamos os símbolos:
⊂ : Está contido
⊂/ : Não está contido
⊃ : Contém
⊃/ : Não contém
Exemplo:
Se você já leu nosso artigo sobre Conjuntos numéricos, sabe que os números naturais e números inteiros podem ser usados como exemplos dessa relação!
Elemento Complementar
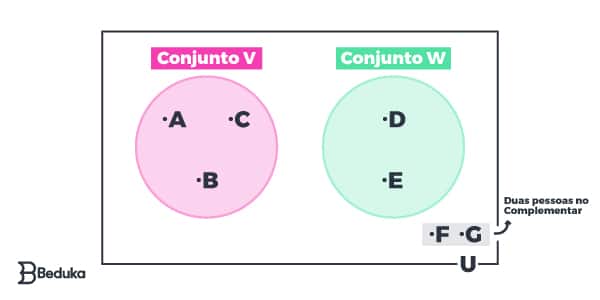
Complementar são todos os elementos que não estão contidos nos conjuntos ou subconjuntos, mas fazem parte do Universo. São aqueles representados no cantinho do retângulo.
Supondo que uma pesquisa entrevistou 7 pessoas e, dessas, 3 responderam que preferem o conjunto V e 2 responderam que preferem o conjunto W. O restante não se identificou com nenhum dos conjuntos, mas fizeram parte da pesquisa. Assim, elas formam o Complementar.
A sua representação por extenso seria: Complementar = {x ∈ U | x ∉ V e x ∉ W}. No gráfico, teríamos a formação da imagem acima.
Operações de conjunto – Exemplos com o Diagrama
As operações básicas entre dois ou mais conjuntos são 3: União, Intersecção e Diferença. Vamos compreendê-las individualmente:
Operação de União (U)
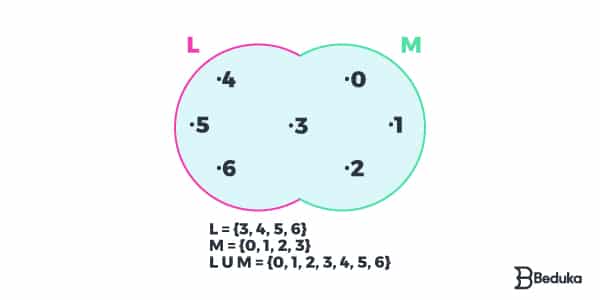
A União é uma operação em que os elementos dos conjuntos são somados. Representamos com o seguinte símbolo: L ⋃ M, então os elementos dos conjuntos L e M se se somam e formam um novo conjunto!
L = {3, 4, 5, 6}
M = {0, 1, 2, 3}
L ⋃ M = {0, 1, 2, 3, 4, 5, 6}
Atenção!
Devemos ter cuidado ao somar conjuntos que possuem alguns elementos iguais! O conjunto L tem 4 elementos e o M também, porém, a sua soma resulta em um conjunto L U M com 7 elementos, pois não podemos contar o mesmo elemento duas vezes!
Operação de Intersecção (∩)
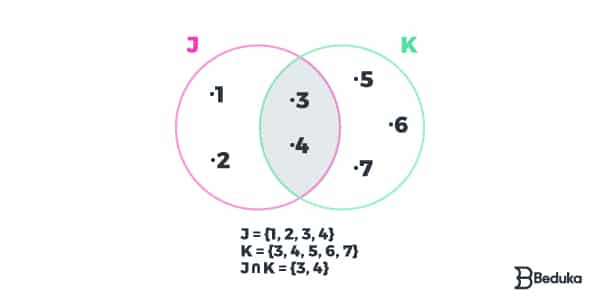
A Intersecção é um novo conjunto numérico formado somente por elementos que pertencem a outros conjuntos ao mesmo tempo.
Considerando os conjuntos J = {1, 2, 3, 4} e K = {3, 4, 5, 6, 7}, temos que os elementos que pertencem ao conjunto J e ao conjunto K, simultaneamente, são:
J ∩ K = {3, 4}
Diferença entre dois conjuntos
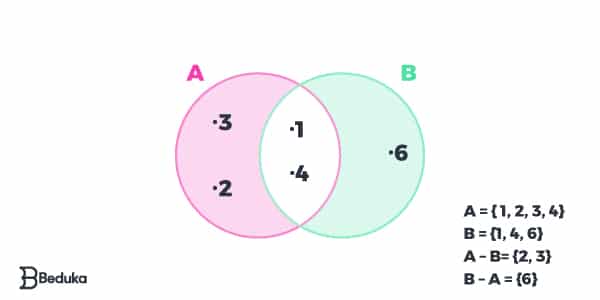
Considere dois conjuntos C e D, a diferença entre eles (C – D) será um novo conjunto formado por elementos que pertencem a C e não pertencem a D.
A = { 1, 2, 3, 4}
B = {1, 4, 6}
A – B= {2, 3}
B – A = {6}
Resolução de Problemas – Exemplo Prático com Diagrama de Venn
Chega de teoria e vamos a um exercício para aplicar os conceitos!
- Foi feita uma pesquisa entre 100 estudantes de uma escola sobre três tipos de filmes: A (ação), B (terror) e (comédia). O resultado obtido foi: 38 estudantes assistem A, 30 assistem B e 27 assistem C. Outros dados relevantes foram captados: 15 assistem A e B, 8 assistem B e C e 19 assistem A e C. Somente 4 assistem os três tipos.
Considerando os dados da pesquisa, quantos estudantes assistem a apenas um tipo de filme?
Solução
Começamos desenhando um diagrama de Venn, em que cada tipo de filme é um conjunto, ou seja, um círculo. O número que vê os três tipos está na intersecção de A, B e C. Assim por diante vamos posicionando os outros valores.
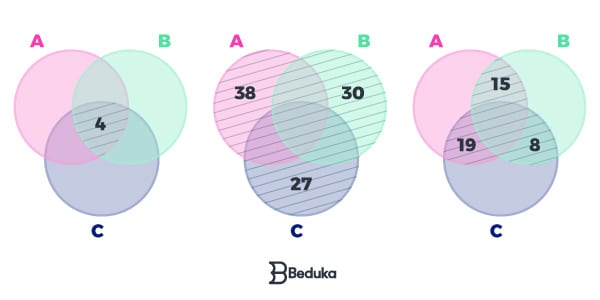
Note que o número de pessoas que assistem os três tipos também está embutido no número de quem assiste dois. Então, para enxergar os valores reais, devemos tirar essas pessoas em comum, para não contá-las duas vezes!
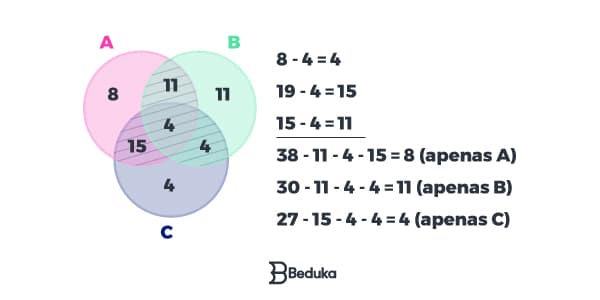
Agora que conhecemos o número real de cada parte do diagrama, podemos calcular o número de estudantes que assiste apenas um tipo, somando os valores de cada conjunto. Assim, temos:
Nº = 11 + 8 + 4 = 23
Ou seja, 23 pessoas assistem apenas 1 tipo de filme!
Gostou do nosso artigo sobre o Diagrama de Venn? Resumo completo! Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





