A função de Segundo Grau é temida por muita gente só porque tem muitos “x” e o expoente “2”. Só que não precisa ser assim… Primeiro que ela sempre cai nos vestibulares, então você vai ter que encarar uma hora. Segundo que a gente te explica tudo o que você precisa saber de uma forma fácil. Duvida? Vem ver!
Neste resumo, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:
- Afinal, o que é uma função?
- O que é uma Função de 2° Grau?
- Quais são os coeficientes dela e a sua forma fatorada?
- Como é o gráfico da Função Quadrática?
- Como fazer o gráfico da Função de Segundo Grau em 2 passos!
- Como encontrar as coordenadas do vértice da parábola?
- Quais são as propriedades das raízes?
Escolher qual curso fazer é sempre um desafio, concorda? Por isso, o Beduka tem um Raio-x que analisa sua personalidade e mostra as carreiras que mais combinam com você!
Afinal, o que significa “Função”?
Você já ouviu a expressão “Eu não vivo em função de você”?
Ela traz a ideia de que existe (ou não) uma dependência entre duas pessoas. E na matemática “função” significa que há uma dependência entre dois valores!
Quando nós sabemos um valor, escrevemos o número que representa exatamente a quantidade. Mas e quando nós não sabemos? Usamos as incógnitas!
As incógnitas são valores que você ainda não conhece e está procurando. Por isso, vai ser representado por uma letra (normalmente usamos “x” e “y”).
As coisas funcionam assim: há um conjunto chamado domínio (D) onde estão todos os possíveis valores de x. Também tem um outro conjunto chamado contradomínio (CD) onde estão todos os possíveis valores de y.
Em outras palavras, estamos dizendo que os valores de x vão determinar qual valor que o y assumirá. Aqui está a dependência, percebeu?
Então, quando escolhermos um valor para x e ele determinar o resultado y, podemos dizer que esse resultado pertence ao conjunto das Imagens (I). As imagens são os elementos do CD que foram definidos.
Tranquilo até aqui? Bora para o assunto principal então:
O que é uma Função de 2° Grau?
Agora você deve estar se perguntando quem determina essa relação entre o x e o y que falamos acima. Bem, a ponte que vai relacionar uma coisa com a outra é a lei de formação, ela é como uma fórmula.
Cada tipo de função tem a sua própria lei de formação, e agora vamos conhecer a da Função do Segundo Grau:
f(x) = ax² + bx + c
Ela tem esse nome porque tem que ter pelo menos uma variável x elevada a 2.
Onde está o y?
Calma! O y também pode ser representado como f(x) quando estamos escrevendo uma função. Então podemos dizer f(x) = ax² + bx + c ou y = ax² + bx + c. Dá no mesmo!
E o que são as letras “a” e“b” e “c”? Cadê os números?
É isso que você vai descobrir agora, mas vamos por partes:
Quais são os elementos da lei de formação da função do 2° Grau?
A lei de formação da Função de 2° Grau é apenas a estrutura básica que as funções desse tipo vão seguir. Na realidade, elas aparecem com números mesmo.
Veja alguns exemplos:
- y = 3x² -4x + 5 (note que a = 3 e b = -4 e c = 5)
- f(x) = -x² + 5x -2 (note que a = -1 e b = 5 e c = -2)
Por se tratar de uma equação de grau 2, também podemos reescrever as funções na sua forma fatorada.
A lei geral da Função de Segundo Grau é f(x) = ax² + bx + c, já a sua forma fatorada é:
f(x) = a (x – x1) (x – x2)
Você deve estar se perguntando que x1 e x2 que é esse, né? Vamos entender agora!
Quantas raízes a função de Segundo Grau tem?
Um termo matemático que é muito importante saber é o conceito de “raiz”. Dizemos que um número é a raiz da função quando ele torna a função nula. Ou seja, é o valor que colocaremos em x e fará com que o resultado y seja 0.
A função de primeiro grau tem uma raiz só. Mas a função de Segundo grau pode ter até 2 raízes!
Um matemático indiano chamado Bhaskara criou uma fórmula para conseguirmos resolver as equações de segundo grau. Você já deve ter visto ela:
É feio porque tem muita letra, mas é simples. Você deve pegar a função de referência e ir substituindo os valores numéricos que aparecem no lugar de a, b e c.
Tem um macete para saber quantas raízes uma função de 2° Grau terá, é só olhar o valor do discriminante (Δ):
- Se Δ = 0, só terá uma 1 raiz (valor de x que zera a função).
- Se Δ > 0 (número positivo), haverá 2 raízes distintas.
- Se Δ < 0 (número negativo), não haverá raízes reais.
A última coisa que precisamos saber é o nome, os detalhes e as condições das letras “a” e “b” e “c”, além do que elas significam:
Coeficiente “a” na Função de 2° Grau
É o número que multiplica o “x²” e vai ser importante na hora de desenhar o gráfico dessa função. Vamos mostrar no próximo tópico!
Perceba que o “a” nunca pode valer 0. Se isso acontecer, o “x²” também será 0 e não existirá Função do Segundo Grau!
Nós sabemos que é muita coisa para lembrar. Por isso fizemos um Plano de Estudos gratuito! Com ele você conseguirá encaixar uma rotina eficaz de estudos junto aos demais afazeres do dia.
Agora vamos continuar:
Coeficiente “b” na Função do 2° Grau
É o número que multiplica o “x” e também vai ser importante na hora de desenhar o gráfico dessa função. Vamos mostrar no próximo tópico!
Perceba que o “b” pode valer 0. Se isso acontecer, teremo uma função onde há apenas uma incógnita, o “x²”.
Coeficiente “c” na Função de Segundo Grau
É o número que não interfere diretamente no x2 ou no x, porque não multiplica nada. Sua influência será apenas no resultado y. Por isso, ele também pode valer 0 e pode ser chamado de termo independente.
Como você deve estar esperando, ele também tem um papel importante na hora de desenhar o gráfico.
Vamos ver, então, o que é que tem de tão especial nesse gráfico:
Como é o gráfico da Função de Segundo Grau?
Já vamos te contar que o gráfico da Função do Segundo Grau tem sempre o formato de uma Parábola.
Além disso, os elementos da lei de formação podem nos dar pistas sobre esse gráfico:
- Se “a” for um número positivo (a > 0), a abertura da parábola estará para cima.
- Se “a” for um número negativo (a < 0), a abertura da parábola estará para baixo.
- Se “b” for um número positivo (b > 0), o braço de parábola que corta o eixo y estará no sentido crescente.
- Se “b” for um número negativo (b < 0), o braço de parábola que corta o eixo y estará no sentido decrescente.
- Se “b” for nulo (0), a parábola está com o vértice sobre o eixo y.
- O “c” indica em qual ponto do eixo y o braço de parábola cruza. Podemos dizer que em toda função desse tipo passará por um ponto (0,c) no gráfico.
Nós sabemos que tudo isso pode parecer teórico demais. Então já fizemos um artigo só com exercícios de Função do Segundo Grau. E sim, eles têm gabarito!
Agora vamos te ensinar como faz para construir esse gráfico:
Como construir o Gráfico da Função do Segundo Grau em 2 passos?
Na realidade, é só estipular valores para x, encontrar quais são os valores de y para ele e formar pares ordenados. Aí você põe tudo no Plano Cartesiano, liga os pontos e está feito!
Quer um exemplo? Vamos construir o gráfico da função y = x² + x:
1. O primeiro passo é atribuir valores a x, e depois calcular o valor correspondente de y. Jogando os valores de x na equação y = x² + x, nós vamos encontrar os pares:
| x | y |
| -3 | 6 |
| -2 | 2 |
| -1 | 0 |
| 0 | 0 |
| 1 | 2 |
| 2 | 6 |
2. Depois, com os valores de x e y, ligamos os pontos correspondentes no plano cartesiano:
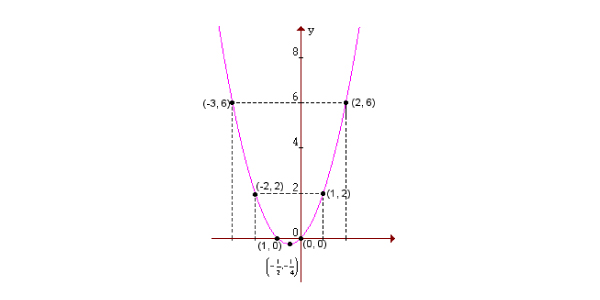
- Só de bater o olho na lei de formação, nós já podíamos esperar que a abertura da parábola fosse para cima, já que o “a” vale 1 (é positivo).
- Também podemos conferir que, de fato, o braço da parábola que cruza o eixo y está no sentido crescente, já que o “b” vale 1 e é positivo.
- Por fim, vemos que o “c” tinha um valor nulo na lei de formação. Realmente, o gráfico toca o eixo” “y no ponto 0!
Como encontrar as coordenadas do vértice da Parábola?
A pontinha da parábola é chamada de vértice, é o local onde ela muda o seu sentido, é onde passa o eixo de simetria.
Por ser um local estratégico, muitas questões envolvem o cálculo das coordenas desse ponto. Inclusive, o Beduka tem um Simulado Enem Gratuito onde você encontra esse tipo de questão.
Perceba que:
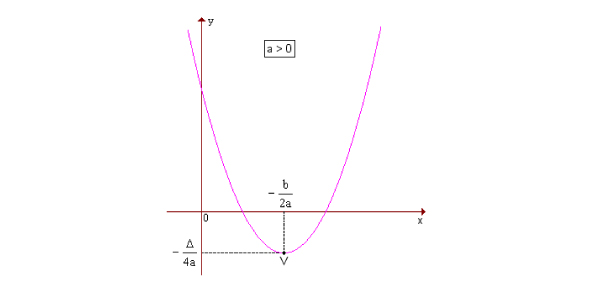
- Quando a > 0, a parábola tem concavidade voltada para cima e um vértice que é o valor mínimo da função.
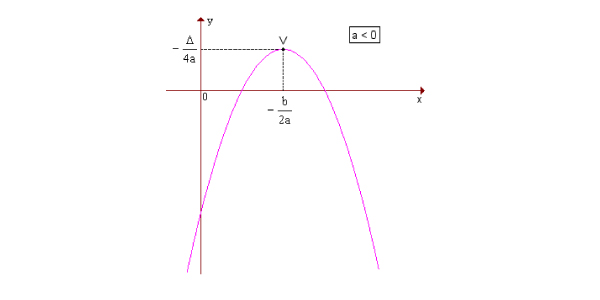
- Quando a < 0, a parábola tem concavidade voltada para baixo e um vértice que é o valor máximo da função.
O vértice V pode ser localizado pelo par de coordenadas (Xv e Yv). Existem fórmulas para achar cada um deles, e elas envolvem os coeficientes da lei de formação:
Xv = – b/2a
Yv = – Δ/4a
Veja os gráficos:
Quais são as propriedades das raízes?
Por último mas não menos importante, precisamos falar de duas propriedades que existem! São duas fórmulas que fucnionam como um macete:
- Propriedade Soma de Raízes: x1 + x2 = -b/a
- Propriedade Produto de Raízes: x1 . x2 = c/a
Gostou de conhecer mais sobre a Função do Segundo Grau? Agora é pôr a mão na massa para não deixar essas dicas serem em vão!
Só mais uma coisinha: no Instagram do Beduka você encontra post e dicas diárias para ajudar os vestibulandos nos estudos e nos seus sonhos de carreira. Vai lá conferir!





