A Função do Segundo Grau é representada pela fórmula f(x) = ax2 + bx+ c – onde “a”, “b” e “c” pertencem ao conjunto dos números reais, e “a” é diferente de zero. Os gráficos podem mudar de acordo com a curvatura da parábola. Leia o artigo e teste os seus conhecimentos com os exercícios de função do segundo grau.
A matemática deixa muitos estudantes de cabelo em pé, por ela ser muito cobrada no Enem e em outros diversos vestibulares. Dentro da matemática, existe a Função do Segundo Grau e o seu entendimento é importante para compreender os gráficos e conseguir realizar os exercícios.
Função do Segundo Grau
A função na matemática possui como característica o domínio e imagem, sendo a imagem dada pelos valores f(x) ou y dentro da função. Os valores dependem do domínio, assim, é possível concluir que x é um termo independente e y é o termo dependente, pois depende do domínio.
A função do segundo grau pode ser chamada de função quadrática ou função polinomial do segundo grau. Ela também pode ser apresentada com até duas raízes reais.
A fórmula que representa a função do segundo grau é diferente da fórmula do primeiro grau, por causa das sua incógnitas.
Veja a fórmula da função do segundo grau:
f(x) = ax2 + bx+ c
Sendo:
a = número real diferente de zero.
b = número real
c = número real
Gráfico
A função do segundo grau é representada por um gráfico, sendo formada por uma curva denominada parábola. É importante entender o gráfico dessa matéria para conseguir fazer os exercícios de função do segundo grau.
O gráfico pode ter duas representações diferentes, se a função quadrática for y = ax² + bx + c, teremos:
- A parábola com a concavidade voltada para cima se a for maior que zero. (Sorriso)
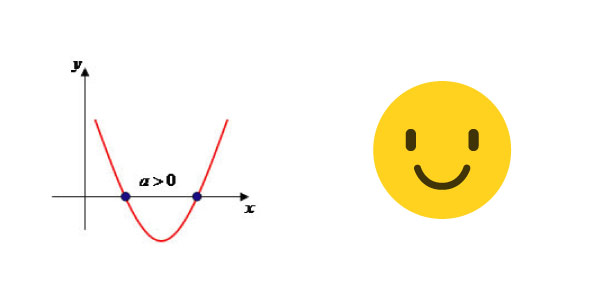
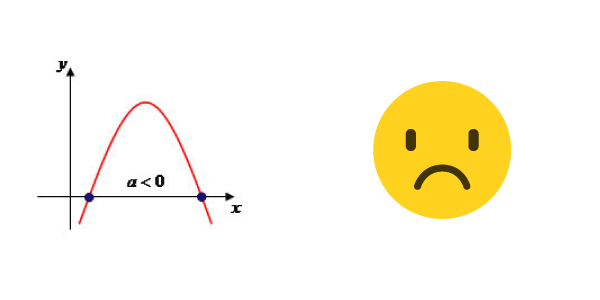
- A parábola com a concavidade voltada para baixo se a for menor que zero. (Boquinha triste)
Baixe o melhor plano de estudos gratuito que você encontrará na internet.
Exercícios de Função do Segundo Grau
1- (ANGLO) – O vértice da parábola y = 2×2 – 4x + 5 é o ponto
a) (2, 5)
b) (1, -3)
c) (-1, 11)
d) (3, 1)
e) (1, 3)
2 – (ANGLO) – A função f(x) = x2 – 4x + k tem o valor mínimo igual a 8. O valor de k é:
a) 8
b) 10
c)12
d) 14
e) 16
3 – (ANGLO) – Se o vértice da parábola dada por y = x2 – 4x + m é o ponto (2, 5), então o valor de m é:
a) 0
b) 5
c) -5
d) 9
e) -9
4 – (VUNESP) – A parábola de equação y = ax2 passa pelo vértice da parábola y = 4x – x2.
Ache o valor de a:
a) 1
b) 2
c) 3
d) -1
e) nda
5 – (METODISTA) – O valor mínimo da função f(x) = x2 – kx + 15 é -1. O valor de k, sabendo que k < 0 é:
a) -10
b) -8
c) -6
d) -1/2
e) -1/8
6 – (ANGLO) – A parábola definida por y = x2 + mx + 9 será tangente aos eixos das abscissas se, e somente se:
a) m = 6 ou m = -6
b) -6 < m < 6
c) -6 £ m £ 6
d) m ³ 6
e) m £ 6
7 – (ANGLO) – Considere a parábola de equação y = x2 – 4x + m. Para que a abscissa e a ordenada do vértice dessa parábola sejam iguais, então m deve ser igual a:
a) -14
b) -10
c) 2
d) 4
e) 6
8 – (VUNESP) – O gráfico da função quadrática definida por y = x2 – mx + (m – 1), onde m Î R, tem um único ponto em comum com o eixo das abscissas. Então, o valor de y que essa função associa ax = 2 é:
a) -2
b) -1
c) 0
d) 1
e) 2
9 – (UFPE) – Planeja-se construir duas estradas em uma região plana. Colocando coordenadas cartesianas na região, as estradas ficam representadas pelas partes dos gráficos da parábola y = – x2 + 10x e da reta y = 4x + 5, com 2 £ x £ 8. Qual a soma das coordenadas do ponto representando a interseção das estradas?
a) 20
b) 25
c) 30
d) 35
e) 40
10 – (FATEC) – A distância do vértice da parábola y= -x2 + 8x – 17 ao eixo das abscissas é:
a) 1
b) 4
c) 8
d) 17
e) 34
11 – (MACK) – O gráfico da função real definida por y = x2 + mx + (15 – m) tangencia o eixo das abscissas e corta o eixo das ordenadas no ponto (0, k). Se a abscissa do vértice da parábola é negativa, k vale:
a) 25
b) 18
c) 12
d) 9
e) 6
12 – (FUVEST) – Os pontos (0, 0) e (2, 1) estão no gráfico de uma função quadrática f. O mínimo de f é assumido no ponto de abscissa x = – 1/ 4. Logo, o valor de f(1) é:
a) 1/10
b) 2/10
c) 3/10
d) 4/10
e) 5/10
13 – (FATEC) – O gráfico de uma função f, do segundo grau, corta o eixo das abcissas para x = 1 e x = 5. O ponto de máximo de f coincide com o ponto de mínimo da função g, de R em R, definida por g(x) = (2/9) x2 – (4/3)x + 6. A função f pode ser definida por
a) y = -x² + 6x + 5
b) y = -x² – 6x + 5
c) y = -x² – 6x – 5
d) y = -x² + 6x – 5
e) y = x² – 6x + 5
14 – (UFPE) – O gráfico da função quadrática y = ax2 + bx + c, x real, é simétrico ao gráfico da parábola y = 2 – x2 com relação à reta de equação cartesiana y = -2. Determine o valor de 8ª + b + c.
a) – 4
b) 1/2
c) 2
d) 1
e) 4
15 – (UEL) – A função real f, de variável real, dada por f(x) = -x2 + 12x + 20, tem um valor
a) mínimo, igual a -16, para x = 6
b) mínimo, igual a 16, para x = -12
c) máximo, igual a 56, para x = 6
d) máximo, igual a 72, para x = 12
16 – (UFMG) – Nessa figura, está representada a parábola de vértice V, gráfico da função de segundo grau cuja expressão é
a) y = (x² /5) – 2x
b) y = x² – 10x
c) y = x² + 10x
d) y = (x²/5) – 10x
e) y = (x² /5) + 10x
Temos um Simulado Enem online 100% gratuito que te ajuda a se preparar para a prova do ENEM. Você pode fazer os exercícios de acordo com o dia, com o caderno de prova ou você pode personalizá-lo do seu próprio jeito.
Confira as respostas dos exercícios de função do segundo grau com o nosso gabarito abaixo.
Respostas dos Exercícios de Função do Segundo Grau
Exercício resolvido da questão 1
e) (1, 3)
Exercício resolvido da questão 2
c)12
Exercício resolvido da questão 3
d) 9
Exercício resolvido da questão 4
a) 1
Exercício resolvido da questão 5
b) -8
Exercício resolvido da questão 6
a) m = 6 ou m = -6
Exercício resolvido da questão 7
e) 6
Exercício resolvido da questão 8
d) 1
Exercício resolvido da questão 9
c) 30
Exercício resolvido da questão 10
a) 1
Exercício resolvido da questão 11
d) 9
Exercício resolvido da questão 12
c) 3/10
Exercício resolvido da questão 13
d) y = -x² + 6x – 5
Exercício resolvido da questão 14
c) 2
Exercício resolvido da questão 15
c) máximo, igual a 56, para x = 6
Exercício resolvido da questão 16
a) y = (x² /5) – 2x
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





