Os 14 melhores exercícios de Trigonometria com gabarito!

A trigonometria no triângulo retângulo é algo que os estudantes até dão conta de usar, mas quando falamos na outra parte (Lei dos Senos e Cossenos) parece que tudo complica! Fique tranquilo, vamos te mostrar um resumo simples e fácil. Depois você pode treinar com os melhores exercícios de Trigonometria. Tem gabarito!

Neste artigo, você encontrará todos os temas abaixo. Clique em um dos tópicos para ir direto ao conteúdo da sua escolha:

• O que é Trigonometria?
• Trigonometria no Triângulo retângulo: Seno, Cosseno e Tangente.
• Teoria Euclidiana: trigonometria fora do triângulo retângulo (Lei dos senos, cossenos e tangente).
• Lista de exercícios de Trigonometria!
• Gabarito dos exercícios de Trigonometria.

Você tem dúvida sobre qual profissão seguir? O Raio-X do Beduka te ajuda a fazer uma análise pessoal e mostra quais carreiras mais combinam com o seu perfil!

O que é Trigonometria?

Muita gente tem birra da trigonometria. Mas ela é apenas uma ferramenta matemática que leva em conta os ângulos e os lados que o formam.

Você lembra das relações de semelhança nos triângulos? A ideia que a trigonometria traz é parecida: sempre que pegarmos dois valores específicos e dividimos eles, nos dará um mesmo resultado.

Até aqui tudo bem? Então vamos para a parte prática:

Trigonometria no triângulo retângulo

Antes de tudo precisamos lembrar as características do triângulo retângulo:

• É preciso que um de seus ângulos seja 90° (reto).
• A soma de todos os três ângulos resulta em 180°.
• O lado maior é o lado oposto ao ângulo reto, chamado de hipotenusa.
• Os outros dois lados são chamados de cateto.

Simples né? Há mais de 200 resumos como esse no Instagram do Beduka!

O que é Seno, Cosseno e Tangente?

A trigonometria diz que, no triângulo retângulo, podemos estabelecer três relações:

• Seno: é um valor específico encontrado para cada ângulo, quando pegamos o cateto (lado) oposto a ele e dividimos pela hipotenusa.
• Cosseno: é um valor específico encontrado para cada ângulo, quando pegamos o lado que encosta nele (adjacente) e dividimos pela hipotenusa.
• Tangente: é um valor específico encontrado para cada ângulo, quando pegamos o cateto oposto e dividimos pelo adjacente.

Viu? Tudo tranquilo. Podemos colocar essas informações em fórmulas:

• Sen x° = cat. oposto / hipotenusa
• Cos x° = cat. adjacente / hipotenusa
• Tg x° = cat. oposto / cat. adjacente

Nós já fizemos um artigo te contanto todos os macetes para decorar essas fórmulas. Tem até um quadro com os ângulos notáveis para você usar de resumo e um exemplo de como usar isso na questão!

Também é importante saber sobre as Funções Trigonométricas.

Teoria Euclidiana: trigonometria em outras figuras

Saber as teorias euclidianas é importante para realizar os exercícios sobre trigonometria.

Isso porque, muitas vezes, as figuras da pergunta não serão triângulos retângulos. Aí não poderemos usar as fórmulas que vimos acima.

Nesses casos, devemos usar as três leis trigonométricas:

Lei dos Senos

Essa lei mostra que quando dividimos o valor de um lado pelo seno do seu ângulo posto, o valor é constante. Se fizermos isso com cada lado, o resultado será sempre o mesmo no contexto daquele triângulo.

Isso pode ser resumido em:

a/senA = b/senB = c/senC

Exemplo:

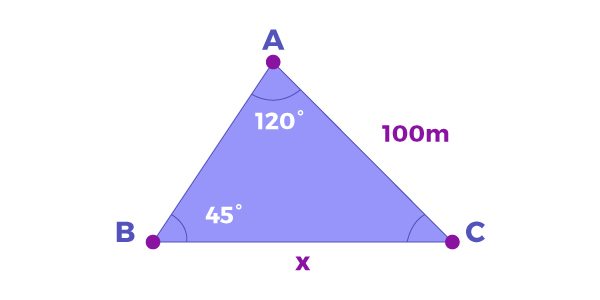
Pergunta: encontre o valor de x no triângulo acima.

Resposta: Nós queremos achar o valor do lado x e temos um ângulo oposto a ele 120°. Também temos o valor de um lado 100m e o ângulo oposto a ele 45°.

Pela lei dos senos, sabemos que a divisão desses valores deve ser igual (constante).

Então podemos calcular o valor da constante usando o lado e o ângulo que já temos. Depois, igualamos ao ângulo e lado que buscamos.

O segundo jeito é já escrever uma equação diretamente:

100 / sen 45° = x / sen120°

100 / √2/2 = x / √3/2

100/ 0,7 = x / 0,87

142,86 . 0,87 = x

124,29 = x (aproximadamente)

Lei dos Cossenos

Essa lei mostra que o quadrado de um dos lados do triângulo equivale à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.

Confuso né? Dá pra resumir em um fórmula para cada lado:

a² = b² + c² – 2.b.c

b² = a² + c² – 2.a.c

c² = a² + b² – 2.a.b

Exemplo:

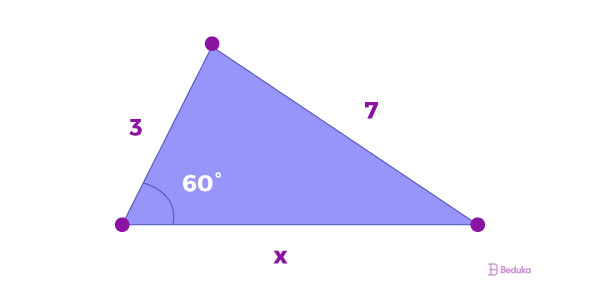
Usando a lei dos cossenos, encontre o valor do segmento x no triângulo abaixo:

7² = x² + 3² – 2·3·x·cos60

49 = x² + 9 – 6·x·0,5

49 = x² + 9 – 3·x

x² – 3x – 40 = 0

Lei das Tangentes

Essa lei apresenta a relação entre as tangentes de dois ângulos de um triângulo e os comprimentos dos lados opostos da tangente.

Sua fórmula é:

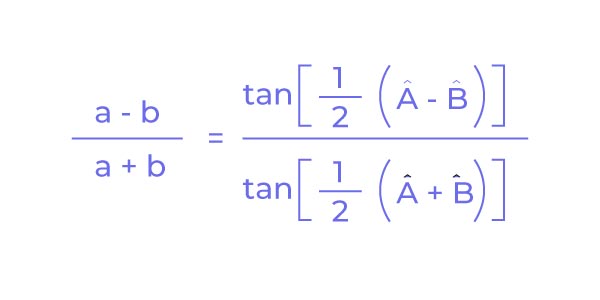
Quando você terminar as questões de Trigonometria, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil.

Exercícios de Trigonometria

Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.

Parabéns por ter lido até aqui!

Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.

Questão 1 – Epcar / 2016

As cidades A, B e C situam-se às margens de um rio e são abastecidas por uma bomba situada em P, conforme figura abaixo.

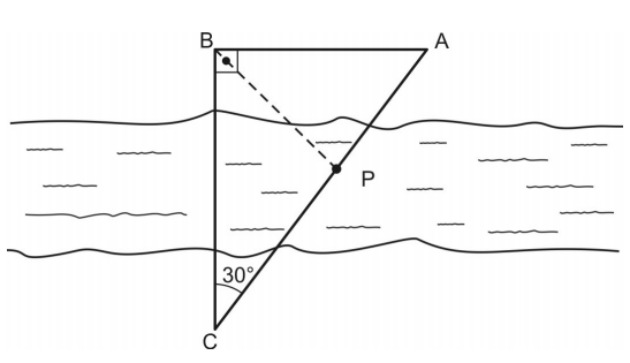
Sabe-se que o triângulo ABC é retângulo em B e a bissetriz do ângulo reto corta AC no ponto P. Se BC = 6√3 km, então CP é, em km, igual a

a) 6 +√3.

b) 6(3 − √3 ).

c) 9 √3 − √2.

d) 9(√ 2 − 1).

Questão 2 – Enem – 2011

Para determinar a distância de um barco até a praia, um navegante utilizou o seguinte procedimento: a partir de um ponto A, mediu o ângulo visual α fazendo mira em um ponto fixo P da praia. Mantendo o barco no mesmo sentido, ele seguiu até um ponto B de modo que fosse possível ver o mesmo ponto P da praia, no entanto sob um ângulo visual 2α. A figura ilustra essa situação:

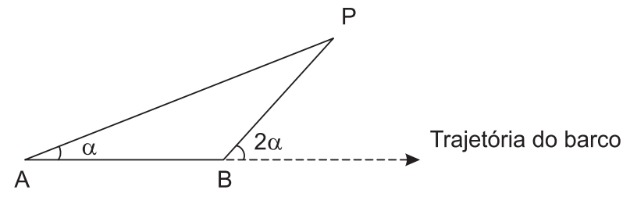
Suponha que o navegante tenha medido o ângulo α= 30º e, ao chegar ao ponto B, verificou que o barco havia percorrido a distância AB = 2 000 m. Com base nesses dados e mantendo a mesma trajetória, a menor distância do barco até o ponto fixo P será

a) 1000 m.

b) 1000 √3 m.

c) 2000 √3/3 m.

d) 2000 m.

e) 2000 √3 m.

Questão 3 – (UNICAMP – 2013)

Ao decolar, um avião deixa o solo com um ângulo constante de 15º. A 3,8 km da cabeceira da pista existe um morro íngreme. A figura abaixo ilustra a decolagem, fora de escala. Podemos concluir que o avião ultrapassa o morro a uma altura, a partir da sua base, de

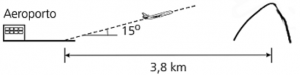
a) 3,8 tan (15°) km.

b) 3,8 sen (15°) km.

c) 3,8 cos (15°) km.

d) 3,8 sec (15°) km.

• Você já fez 20%  das questões sobre Trigonometria. Continue assim!

Questão 4 – (Cesgranrio)

Uma escada de 2m de comprimento está apoiada no chão e em uma parede vertical. Se a escada faz 30° com a horizontal, a distância do topo da escada ao chão é de:

a) 0,5 m.

b) 1 m.

c) 1,5 m.

d) 1,7 m.

e) 2 m.

Questão 5 – (Ufjf)

A uma tela de computador está associado um sistema de coordenadas cartesianas, com origem no canto inferior esquerdo. Um certo programa gráfico pode ser usado para desenhar na tela somente retas de inclinações iguais a 0°, 30°, 45°, 60° e 90° em relação ao eixo horizontal. Então, considerando-se os pontos a seguir, o único que NÃO pode estar sobre uma reta, A PARTIR DA ORIGEM, desenhada por este programa é:

a) (0, 10Ë3).

b) (10Ë3, 0).

c) (10Ë3, 10Ë3).

d) (10Ë3, 5Ë3).

e) (10Ë3, 10).

Questão 6 – (Ufes)

Duas circunferências são tangentes entre si e aos lados de um ângulo. Se R é o raio da maior, r é o raio da menor e o ângulo mede 60°, então

a) R = (3Ë3)r/2.

b) R = 2Ë3r .

c) R = 3Ë3r .

d) R = 2r .

e) R = 3r.

Questão 7 – (Ufsm)

Um estudante de Engenharia vê um prédio do Campus da UFSM construído em um terreno plano, sob um ângulo de 30°. Aproximando-se do prédio mais 40m, passa a vê-lo sob um ângulo de 60°. Considerando que a base do prédio está no mesmo nível do olho do estudante, então a altura h do prédio é igual a

a) 30Ë3 m.

b) 20Ë3 m.

c) 30 m.

d) 10Ë3 m.

e) 28 m.

• Muito bem! Você está na metade dos exercícios sobre Trigonometria!

Questão 8 – (Ita)

Um dispositivo colocado no solo a uma distância d de uma torre dispara dois projéteis em trajetórias retilíneas. O primeiro, lançado sob um ângulo šÆ(0,™/4), atinge a torre a uma altura h. Se o segundo, disparado sob um ângulo 2š, atinge-a a uma altura H, a relação entre as duas alturas será:

a) H = 2hd£/(d£-h£).

b) H = 2hd£/(d£+h).

c) H = 2hd£/(d£-h).

d) H = 2hd£/(d£+h£).

e) H = hd£/(d£+h).

Questão 9 – (Fuvest)

O valor de (tg 10°+cotg 10°)sen 20° é:

a) 1/2.

b) 1.

c) 2.

d) 5/2.

e) 4.

Questão 10 – (Fuvest)

Dentre os números a seguir, o mais próximo de sen50° é:

a) 0,2.

b) 0,4.

c) 0,6.

d) 0,8.

e) 1,0.

Questão 11 – (Fuvest)

O menor valor de 1/ (3-cos x), com x real, é:

a) 1/6.

b) 1/4.

c) 1/2.

d) 1.

e) 3.

• Ufa, estamos quase lá! Faça os três últimos exercícios de Trigonometria!

Questão 12 – (Unesp)

Uma máquina produz diariamente x dezenas de certo tipo de peças. Sabe-se que o custo de produção C(x) e o valor de venda V(x) são dados, aproximadamente, em milhares de reais, respectivamente, pelas funções C(x)=2-cos(x™/6) e V(x)=3(Ë2) sen (x™/12), 0´x´6. O lucro, em reais, obtido na produção de 3 dezenas de peças é

a) 500.

b) 750.

c) 1 000.

d) 2 000.

e) 3 000.

Questão 13 – (Puccamp)

Sobre a função f, de IR em IR, definida por f(x)=cos 3x, é correto afirmar que

a) seu conjunto imagem é [-3; 3].

b) seu domínio é [0; 2™].

c) é crescente para x Æ [0; ™/2].

d) sua menor raiz positiva é ™/3.

e) seu período é 2™/3.

Questão 14 – (Unirio)

Seja f: R ë R, onde R denota o conjunto dos números reais, uma função definida por f(x)=[3/(4+cosx)]+1. O menor e o maior valor de f(x), respectivamente, são:

a) 1, 6 e 2.

b) 1, 4 e 3.

c) 1, 6 e 3.

d) 1, 4 e 1,6.

e) 2 e 3 .

• Parabéns, você fez todas as questões sobre Trigonometria! Confira o gabarito logo abaixo:

Respostas dos Exercícios sobre Trigonometria

Exercício resolvido da questão 1

b) 6(3 − √3 ).

Exercício resolvido da questão 2

b) 1000 √3 m.

Exercício resolvido da questão 3

a) 3,8 tan (15°) km.

Exercício resolvido da questão 4

b) 1 m.

Exercício resolvido da questão 5

d) (10Ë3, 5Ë3).

Exercício resolvido da questão 6

e) R = 3r.

Exercício resolvido da questão 7

b) 20Ë3 m.

Exercício resolvido da questão 8

a) H = 2hd£/(d£-h£).

Exercício resolvido da questão 9

c) 2.

Exercício resolvido da questão 10

d) 0,8.

Exercício resolvido da questão 11

b) 1/4.

Exercício resolvido da questão 12

c) 1 000.

Exercício resolvido da questão 13

e) seu período é 2™/3.

Exercício resolvido da questão 14

a) 1, 6 e 2.

Gostou dos nossos exercícios de Trigonometria? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, mensalidade e muito mais.

Experimente agora!