O que é Seno, Cosseno e Tangente? São relações matemáticas que encontramos dividindo lados por ângulos. Pode parecer meio vago e sem sentido mas, neste artigo, vamos te mostrar com imagens e exemplos todos os detalhes: como fazer o cálculo, para que ele serve e o que significam.
Neste artigo sobre o que é Seno, Cosseno e Tangente você encontrará:
- Triângulo retângulo (introdução)
- O que é Seno, Cosseno e Tangente
- Propriedades e observações importantes
- Exemplos numéricos e aplicação (para quê serve)
- Treine para as provas com nosso Simulado online e gratuito! Você pode até personalizá-lo com as matérias que mais precisa!
Triângulo retângulo e trigonometria
Antes de falar propriamente sobre o que é Seno, Cosseno e Tangente, precisamos relembrar algumas características do triângulo Retângulo, pois vamos precisar delas lá na frente:
- O triângulo retângulo apresenta um ângulo interno reto (90º).
- O lado oposto ao ângulo de 90º é chamado de hipotenusa e os outros de catetos.
- Dependendo da posição dos catetos em relação ao ângulo, chamamos de oposto ou adjacente.
Por ora, estes detalhes bastam para continuarmos. Mas aqui vai um artigo para saber mais sobre trigonometria no triângulo retângulo!
O que é Seno, Cosseno e Tangente
Visto que já sabemos das características dos triângulos retângulos e que as relações trigonométricas se baseiam na relação entre divisão de ângulos e lados, vamos às definições!
- Falando em trigonometria, saiba como transformar graus em radianos.
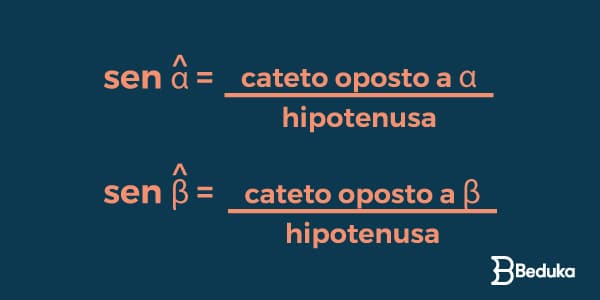
O que é Seno
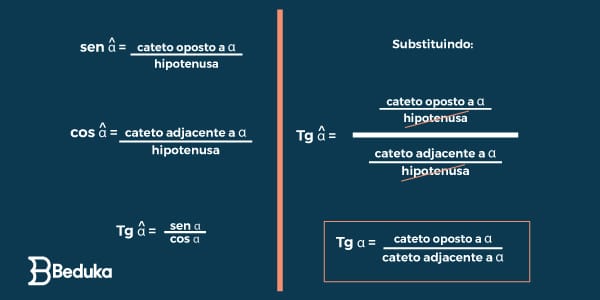
O Seno de qualquer ângulo é o valor que encontramos ao dividir o seu cateto oposto pela hipotenusa. Veja a fórmula do Seno:
- De onde veio essa fórmula? O que isso significa no ciclo trigonométrico?
Uma outra definição para Seno é:
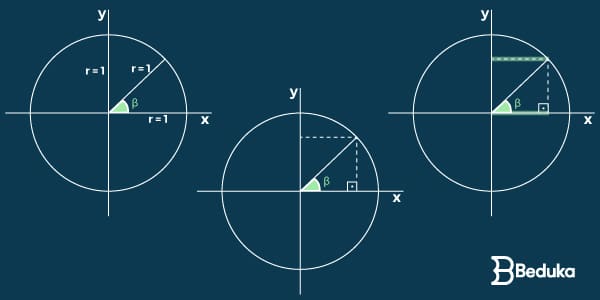
“Projeção da medida do ângulo no eixo das coordenadas (eixo y).”
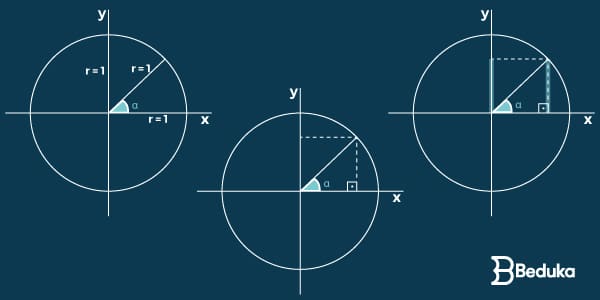
Vamos relembrar que no Ciclo trigonométrico o raio é sempre unitário, ou seja, vale 1. Por isso, o seno sempre será um número entre 0 e 1.
No ciclo trigonométrico, a projeção do valor do seno no eixo y é igual ao tamanho do cateto oposto (observe a imagem).
Com base nisso, os matemáticos perceberam que estas medidas só eram iguais porque a hipotenusa vale 1 (lembre-se que o raio é unitário no ciclo).
Portanto, se tivéssemos um triângulo fora do ciclo trigonométrico, não poderíamos dizer que o valor do seno é igual ao do cateto oposto.
Diante disso, foi preciso estabelecer uma fórmula genérica que se aplique tanto aos triângulos do ciclo quanto aos de fora.
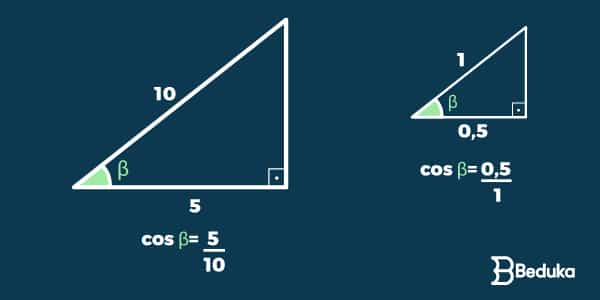
Daí surgiu a fórmula. Ao estabelecer que o valor do seno é o cateto oposto dividido pela hipotenusa, o resultado se adequa a qualquer medida que um triângulo retângulo possuir. Afinal, a razão entre 8 e 4 é a mesma que a razão entre 64 e 32.
IMPORTANTE
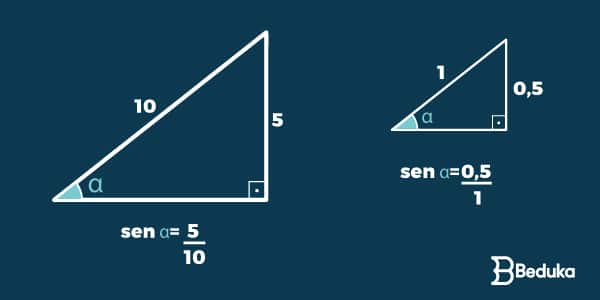
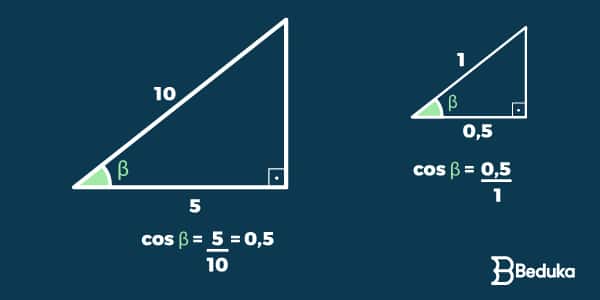
Observe que o resultado de ambos os senos são iguais.
Isso ocorreu pois os triângulos são semelhantes: apesar de terem lados diferentes, como essa diferença é a mesma (constante), seus ângulos são iguais.
Daí, tiramos mais uma conclusão: o valor do seno é essencialmente determinado pelo valor do ângulo, e não do lado.
Portanto, os lados podem ter qualquer medida mas um mesmo ângulo sempre terá um mesmo seno.
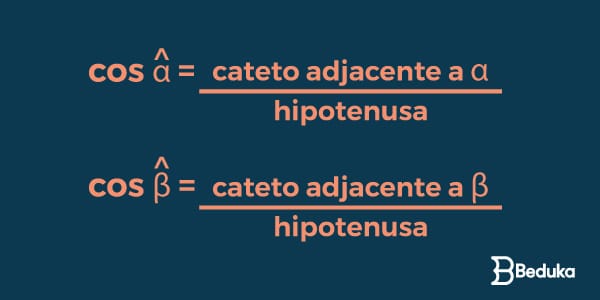
O que é Cosseno
O Cosseno de qualquer ângulo é o valor que encontramos ao dividir o seu cateto adjacente pela hipotenusa. Veja a fórmula do Cosseno:
- De onde veio essa fórmula? O que isso significa no ciclo trigonométrico?
Uma outra definição para Cosseno é:
“Projeção da medida do ângulo no eixo das abscissas (eixo x).”
Vamos relembrar que no Ciclo trigonométrico o raio é sempre unitário, ou seja, vale 1. Por isso, o cosseno sempre será um número entre 0 e 1.
No ciclo trigonométrico, a projeção do valor do cosseno no eixo x é igual ao tamanho do cateto adjacente (observe a imagem).
Com base nisso, os matemáticos perceberam que estas medidas só eram iguais porque a hipotenusa vale 1 (lembre-se que o raio é unitário no ciclo).
Portanto, se tivéssemos um triângulo fora do ciclo trigonométrico, não poderíamos dizer que o valor do cosseno é igual ao do cateto adjacente.
Diante disso, foi preciso estabelecer uma fórmula genérica que se aplique tanto aos triângulos do ciclo quanto aos de fora.
Daí surgiu a fórmula. Ao estabelecer que o valor do cosseno é o cateto adjacente dividido pela hipotenusa, o resultado se adequa a qualquer medida que um triângulo retângulo possuir. Afinal, a razão entre 4 e 2 é a mesma que a razão entre 16 e 8.
IMPORTANTE
Observe que o resultado de ambos os cossenos são iguais.
Isso ocorreu pois os triângulos são semelhantes: apesar de terem lados diferentes, como essa diferença é a mesma( constante), seus ângulos são iguais.
Daí, tiramos mais uma conclusão: o valor do cosseno é essencialmente determinado pelo valor do ângulo, e não do lado.
Portanto, os lados podem ter qualquer medida mas um mesmo ângulo sempre terá um mesmo cosseno.
O que é Tangente
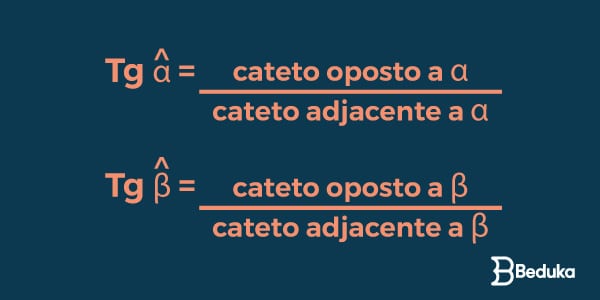
A Tangente de qualquer ângulo é o valor que encontramos ao dividir o seu cateto oposto pelo cateto adjacente. Veja a fórmula da Tangente:
- De onde veio essa fórmula? O que isso significa no ciclo trigonométrico?
Uma outra definição para Tangente é:
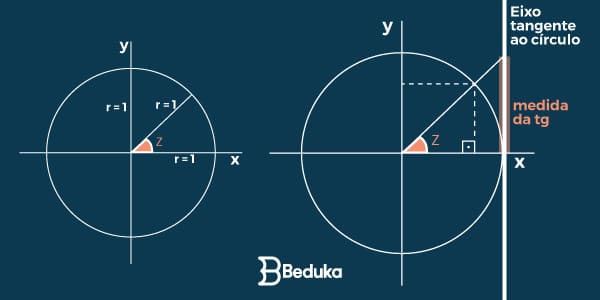
“Projeção da medida do ângulo no eixo tangente ao ciclo trigonométrico”
A tangente não tem um limite mínimo ou máximo de valor, veja no desenho para entender melhor:
Com isso, os matemáticos observaram que para encontrar esse valor que está além do ciclo, era preciso dividir o valor do seno pelo cosseno, pois somente eles possuíam a hipotenusa em comum; e a tangente se dá justamente pelo prolongamento da hipotenusa.
Daí surgiu a fórmula: na hora de fazer os cálculos, obtemos:
IMPORTANTE
Daí, tiramos mais uma conclusão: o valor da tangente é essencialmente determinado pelo valor do ângulo, e não do lado. Pois deriva de seno e cosseno e estes também o são.
Macete
Pra decorar as fórmulas com facilidade:
- Andou de COStas? CA Hi (COSseno = Cateto Adjacente dividido pela Hipotenusa)
- Está SENo roubado? COrHI (SENo = Cateto Oposto dividido pela Hipotenusa)
- Tá Gostoso? CO CA (Tangente = Cateto Oposto dividido pelo Cateto Adjacente)
É fácil memorizar coisas bestas! rsrs
Propriedades e observações importantes
Agora que já sabemos o que é Seno, Cosseno e Tangente; podemos entender algumas propriedades.
Triângulos semelhantes
O valor do Seno, Cosseno e Tangente são determinados pelos ângulos. Logo, em triângulos semelhantes, os valores dessas razões trigonométricas serão iguais porque os ângulos são iguais.
Já explicamos o porquê disso anteriormente.
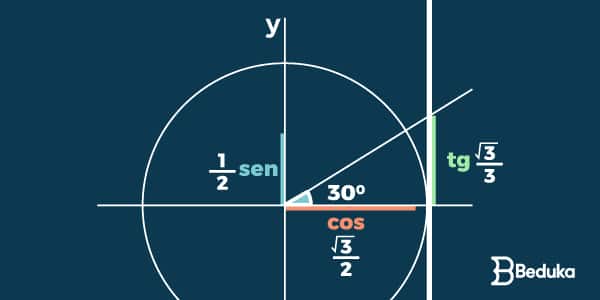
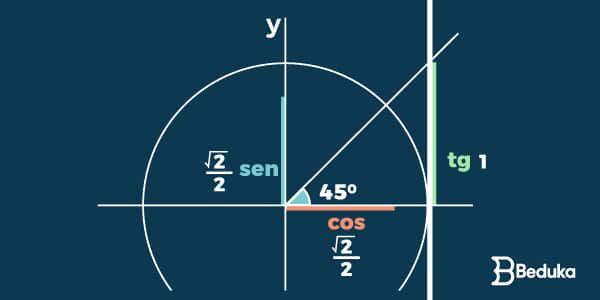
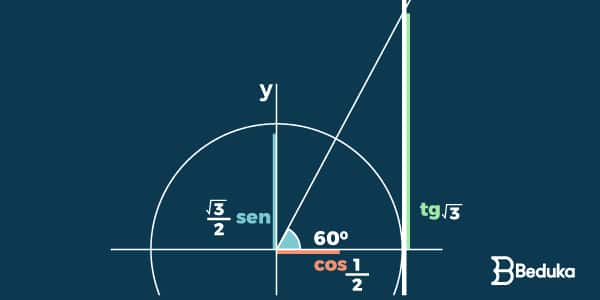
Ângulos Notáveis
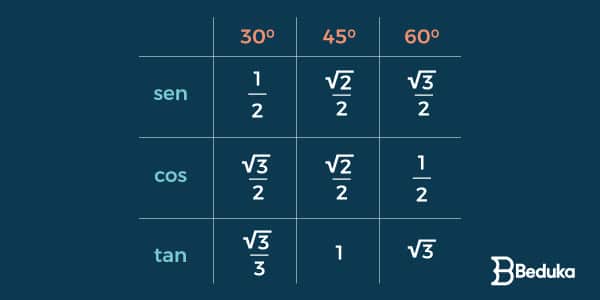
Na matemática, definiu-se que existem 3 ângulos notáveis (30°,45° e 60°), ou seja, ângulos recorrentes e fáceis de se identificar.
Eles são os mais cobrados nas provas e devemos saber os valores de seus Senos,Cossenos e Tangentes de cór.
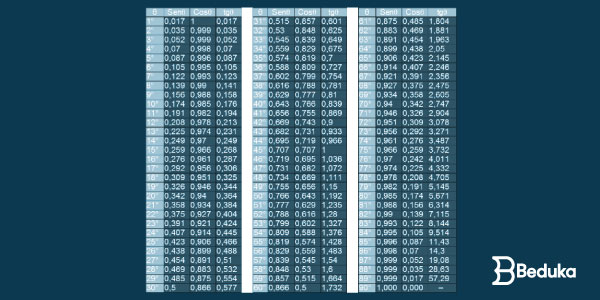
Para isso, há uma tabelinha muito famosa que todo estudante deve saber:
- Você pode encontrar diversas músicas para te ajudar a decorar !
Os demais ângulos não são obrigatórios sabermos. Se o professor cobrar, deverá dar o valor ou a tabela. Se ele der a tabela que contém os valores decimais dos ângulos notáveis, use os valores da tabela. Veja:
Ou ainda, ele pode dar o seno e o cosseno de um ângulo não-notável e pedir os valores do seno e cosseno de seu ângulo complementar. Neste caso, você terá de lembrar da propriedade que veremos a seguir:
Ângulos Complementares
Se você é um aluno atento, deve ter notado que o seno do 30° é igual ao cosseno do 60° e que o cosseno de 30° é igual ao seno do 60°
Aqui temos mais uma propriedade: quando se trata de ângulos complementares ( que somados formam 90°), o seno de um é igual ao cosseno de outro e vice versa.
Quanto à tangente, a relação é o inverso. Veja:
- O mesmo serve para quaisquer ângulos complementares (50° e 40°, 45° e 45°, etc)
Relação trigonométrica fundamental
Esta relação é quase um macete, pois serve quando conhecemos o valor do seno de um ângulo e queremos saber qual é o cosseno deste ângulo, mas nenhuma outra informação foi dada.
Neste caso, não seria possível aplicar as fórmulas clássicas, só poderíamos usar essa relação:
Essa fórmula se originou por meio do uso de teorema de pitágoras. Mas sua demonstração não é essencial para compreendermos as questões. Vamos aos exercícios!
Exemplos numéricos e aplicação
A trigonometria é muito importante não só para resolver as questões das provas mas, principalmente, para o desenvolvimento das ciências exatas, como física e engenharia.
Foi por meio desses cálculos que grande parte das nossas construções estão de pé.
Agora que você já sabe da importância prática dessa área, vamos treinar os exercícios para acabar com qualquer dúvida:
- Se quiser, pode já ir treinando sozinho os outros exercícios de trigonometria!
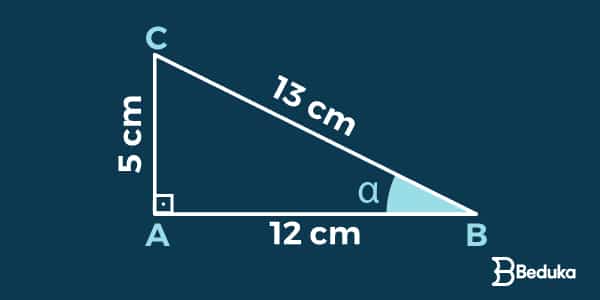
1)Encontre os valores do seno, cosseno e tangente do ângulo do triângulo abaixo.
Primeiro, devemos substituir a medida de cada lado do triângulo nas fórmulas.
Observando a imagem, identificamos que o cateto oposto mede 5 cm, o cateto adjacente mede 12 cm e a hipotenusa é 13 cm.
Logo:
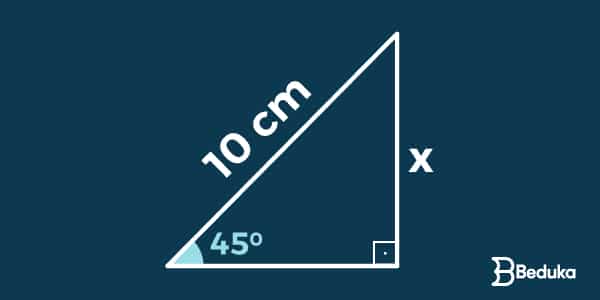
2)Determine o valor de x :
Primeiro, observe quais elementos você já tem e em qual fórmula dá para encaixar de modo que só reste uma incógnita. Esta você consegue calcular manipulando a equação.
Temos a hipotenusa (10 cm) e queremos descobrir x – que é o cateto oposto ao ângulo de 45º. Assim, aplicaremos a fórmula do seno.
Na tabela trigonométrica, o valor do seno de 45.º é igual a 0,7071. Assim:
Logo, o lado x mede 7,071 cm.
Gostou do nosso artigo sobre o que é Seno,Cosseno e Tangente? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





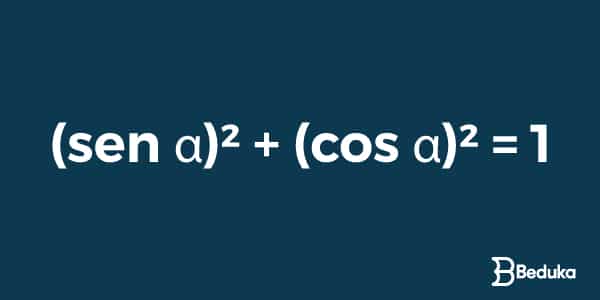



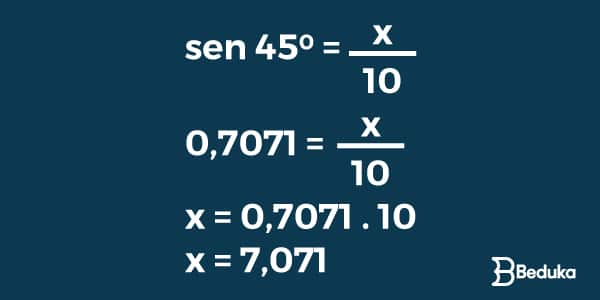



4 Comentários
Até que enfim, até que enfim, alguém DEFINIU seno, cosseno e tangente fora do triângulo retângulo! Os professores e livros didáticos querem empurrar o conceito de tangente na cabeça das pessoas a partir do triângulo retângulo, MAS NÃO DÁ PRA ENXERGAR A BENDITA TANGENTE EM RELAÇÃO AO TRIÂNGULO! E agora, felizmente, apareceram vocês, abordando o assunto sem ofender os neurônios dos seres-humanos. Obrigado.
Hahahahaha! Que bom que gostou do conteúdo, Lívio.
Ainda bem que encontrei esse artigo, eu estava com muita dificuldade para entender o professor ou os vídeos sobre o assunto. Mas graças a vocês posso finalmente compreender como funciona.
Essa é a nossa missão, Yasmin. Ficamos felizes em ajudar.