A equação do 2º grau é caracterizada pela variável “x” estar elevada ao quadrado “²”, por isso, sua fórmula geral é: ax² + bx + c = 0. Para que isso seja verdadeiro, os coeficientes “a”,”b” e “c” devem pertencer ao números reais e o “a” deve ser diferente de 0. O modo mais tradicional de resolver uma equação quadrática é utilizando a fórmula de báskara.
Neste artigo sobre Equação do segundo grau, você encontrará:
- O que é Equação do segundo grau? Definição e termos
- Equação completa e incompleta
- Quantas soluções tem uma equação do segundo grau?
- Como resolver uma equação de segundo grau? Passo a passo – Bháskara e Sistema
- Exemplos resolvidos
- Para entender mesmo essa matéria, você precisa conferir o artigo sobre Função de segundo grau ao final desta leitura!
- Estudando para as provas? Conheça nosso Simulado Enem gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que é Equação do segundo grau? Exemplos
A palavra “Equação” está originalmente relacionada à palavra igualdade, portanto, falar em equação é querer tornar as coisas iguais. Nesta igualdade há números conhecidos e outros desconhecidos.
Muitas vezes as equações estão em forma de polinômios, ou seja, um conjunto de letras e números que formam uma expressão numérica. O valor que não sabemos é chamado de incógnita e ele pode ser representado por qualquer letra, o mais comum é utilizarmos “x”,”y”ou “z”.
- O formato básico de qualquer equação do segundo grau é: ax² + bx + c = 0.
Nela, o x é a nossa incógnita e observe que ele está elevado ao expoente 2, ou seja, é “x ao quadrado”. Ter a incógnita elevada a 2 é o que caracteriza uma equação de segundo grau, por isso ela tem esse nome ou também pode ser chamada de equação quadrática.
O “a” é chamado de coeficiente primário, o “b” é o coeficiente secundário e o “c” é o termo independente. Você ainda pode encontrá-los como quadrático (a), linear (b) e o constante (c)
Esses termos são definidos de acordo com o contexto do problema, e seus números irão compor o cálculo para acharmos quanto vale o “X”.
Atenção!
Em uma equação de segundo grau o “a” nunca pode ser igual a 0. Quando há um número e uma letra juntos, sem nenhum sinal entre eles, significa que há uma multiplicação, assim, o coeficiente “a” está multiplicando o x². Se for a=0, o x² resulta em 0 e deixa de ser uma equação quadrática e passa a ser de primeiro grau!
- Por isso a condição de existência dessa equação é que todos os coeficientes sejam pertencentes ao conjunto dos números reais e “a” diferente de 0!
Exemplos numéricos da equação de segundo grau:
- 2x² +4x – 6 = 0 . Em que a = 2, b =4 e c = – 6
- x² – 5x + 2 = 0 . Em que a =1, b= – 5 e c = 2
- 0,5x² + x –1 = 0 . Em que a = 0,5, b = 1 e c = –1
O que é equação do segundo grau completa e incompleta?
Como você viu, apenas o “a” não pode ser 0. Mas o que acontece se o “b” ou o “c” forem?
A equação do 2º grau será classificada como incompleta quando o valor dos coeficientes b ou c são iguais a 0. Então: b = 0 ou c = 0. A equação só será classificada como completa quando todos os coeficientes são diferentes de 0, ou seja, a ≠ 0, b ≠ 0 e c ≠ 0.
Todos os exemplos dados acima foram de completas, agora vamos aos exemplos das incompletas:
- 2x² – 4 = 0 . Em que: a = 2, b = 0 e c= – 4
- -x² + 3x = 0 . Em que: a = – 1, b = 3 e c = 0
- x² = 0 . Em que: a = 1, b =0 e c =0
Como resolver uma equação de segundo grau?
Para resolver uma equação de segundo grau, precisamos descobrir quanto vale a incógnita, ou seja, o “x”. Quando encontramos um valor numérico para isso, chamamos de “raiz da equação”.
Buscamos esse valor para tornar a igualdade verdadeira, isto é, ao substituir o valor de x na expressão, o resultado deve ser igual a 0. Isso prova que o valor é correto e resolve o problema!
Para fazer esse cálculo, o tradicional é usar a fórmula de Bháskara!
Fórmula de Bhaskara
Bhaskara foi um matemático que descobriu uma fórmula em que qualquer equação de segundo grau pudesse ser resolvida, seja ela completa ou incompleta. Para as incompletas, existem métodos mais rápidos, porém vamos falar do modo universal para você poder usar sempre.
Essa fórmula é representada por:
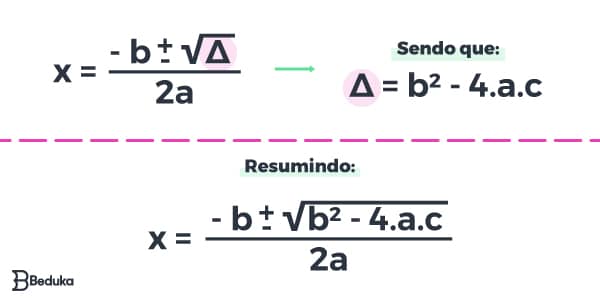
Não se assuste! Só estamos querendo te mostrar que existe uma fórmula dentro da outra…. na primeira opção você enxerga fórmula clássica e basta olhar para equação, identificar o valor numérico dos termos “a”, “b”, “c”, substituir e realizar as operações normalmente!
Porém, o termo delta, representado pelo triângulo, é encontrado por outra fórmula. Então você escolhe se quer fazer um cálculo divido em duas etapas ou uma etapa só (grande)! Fica a seu critério escolher como decorar!
- Atenção!
Observe que existe um sinal de “mais ou menos” que acompanha o valor da raiz quadrada. Qual o motivo disso?
Bem, uma raiz quadrada pode ter dois resultados, um positivo e outro negativo. Isso acontece porque o contrário da raiz quadrada é a potenciação ao quadrado, assim, se fizermos 2² ou -2², o resultado de ambas as contas será 4. Por isso, a raiz de 4 pode ser 2 ou -2!
Por esse motivo, o sinal de “mais ou menos” nos lembra que é necessário prosseguir com 2 contas após descobrir o valor da raiz quadrada, uma com o número negativo e outra com o positivo.
Quantas soluções tem uma equação do segundo grau?
Depois dessa, você deve estar pensando: se há duas contas haverá dois resultados? A resposta é: depende!
O valor de delta (Δ) recebe o nome de discriminante e é ele quem está dentro da raiz quadrada. Conforme vimos, ela pode nos dar 2 valores. Então, um matemático observou que conhecendo o valor do discriminante, podemos realizar algumas afirmações a respeito da quantidade de soluções:
- Se o discriminante for positivo, ou seja, delta maior que zero (Δ > 0) haverá duas soluções diferentes
- Se o discriminante for igual a zero, ou seja, delta igual a zero (Δ = 0), as duas soluções terminam em contas com o mesmo valor, logo, só há de fato uma solução!
- Se discriminante for negativo, ou seja, delta menor que zero (Δ < 0), não existirá uma solução pertencente ao conjunto dos números reais, porque não temos como tirar a raiz de um número negativo! Nesse caso, dizemos que não há solução, mas um conjunto vazio de resultados .
Agora você já entendeu que uma equação de segundo grau pode ter no máximo 2 resultados (duas raízes)!
OBS: não confunda raízes (resultado) com a raiz quadrada (parte da fórmula)!
Resolver equação de segundo grau – passo a passo com exercício resolvido!
Agora chega de teoria e vamos para a prática! Observe a resolução abaixo e depois tente treinar com os exercícios de equação de segundo grau para ver se aprendeu mesmo!
Vamos tomar como base a equação: X²/4 + 5x + 9 = 0
- 1° Passo: Identifique os coeficientes da equação
Sendo assim, teremos a = 1/4, b = 5 e c = 9.
- 2° Passo: Encontre o discriminante
O discriminante de uma equação de segundo grau é indicado pela letra grega delta e pode ser encontrado pela Fórmula de Bháskara. Assim, teremos:
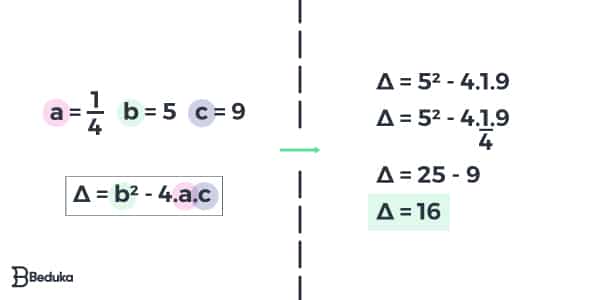
- 3° Passo: Encontre as soluções da equação
Continue usando a fórmula de Bháskara. Lembre-se que basta substituir os valores dos coeficientes e discriminante, além de se atentar para as raízes!

Confira a calculadora de equação do segundo grau e compare o resultado de sua questão com apenas um clique!
Sistema com equação de segundo grau
Ao interpretar um problema, pode ser que você obtenha uma equação com duas incógnitas. Nessa hora surge a dúvida: como resolver?
Mas fique tranquilo porque a questão também dará uma outra equação envolvendo essas mesmas duas incógnitas, então você poderá resolver por meio de um sistema!
Neste caso, a solução será um par ordenado que torne ambas as equações verdadeiras!
O modo de resolver um sistema de equações é sempre o mesmo, independente de ela ser de primeiro ou segundo grau. Assim, você pode optar pelo método da adição ou da substituição!
Não lembra deles? No final do artigo sobre equações de primeiro grau você encontra exemplos resolvidos e passo a passo desses dois métodos!
- Não deixe de ler o artigo sobre Função de segundo grau e treinar os exercícios da equação quadrática, só aí você saberá como funciona o gráfico!
Gostou do nosso artigo sobre equação do segundo grau? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!






8 Comentários
Muito obrigada! Ótima explicação!!
Não foi nada, Lucia! Que bom que pudemos ajudar.
muito boa explicação, agora vou estudar para a prova sem problemas muito obrigada!
Que bom que gostou Giovana! Por nada 🙂
Foi bom gostei muito foi de acordo com as minhas espectativas. Gostaria de ter mais aulas
Tem muito mais conteúdo no site, José. Aproveite!
Como funciona essa fórmula? Como podemos demonstrar/provar ela?
O intuito da equação de segundo grau é descobrir as raízes de de uma função quadrática, ou seja, os valores de x que tornam a função igual a zero. Ela funciona desse jeitinho que trouxemos no texto e pode ser provada tanto por meio da álgebra quanto da geometria.