O Teorema de Tales é uma teoria matemática utilizada para identificar proporção e razão em figuras. Segundo o Teorema, quando houver duas ou mais retas paralelas cortadas por duas ou mais transversais, os segmentos formados serão proporcionais entre si.
Neste artigo sobre o Teorema de Tales, você encontrará:
- O que é Teorema de Tales?
- Onde surgiu o Teorema de Tales e para quê ele serve?
- Como se resolve o Teorema de Tales? Fórmula e exemplo
- Teorema de Tales no triângulo
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que é Teorema de Tales?
O Teorema de Tales é uma teoria matemática que demonstra situações em que há proporção. Segundo o teorema: “A interseção, por duas retas transversais, de um feixe de retas paralelas formam segmentos proporcionais.”
Não entendeu nada? Calma, vamos explicar esses termos agora, mas antes dê uma olhada no desenho:
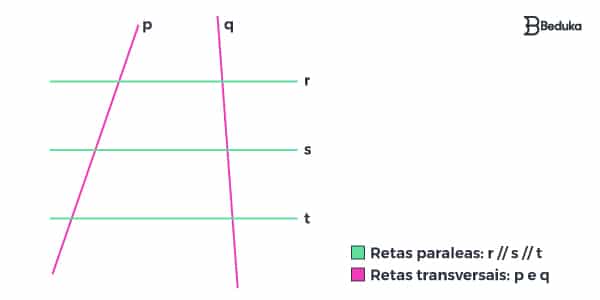
Na imagem acima, você leu na legenda que as retas “r”, “s” e “t” são paralelas, ou seja, se você continuar o desenho delas, prolongando as retas, elas nunca se cruzarão! Isso acontece porque estão perfeitamente alinhadas entre si (r // s // t.)
Já as retas “p” e “q” são chamadas de transversais, porque cortam as retas paralelas em determinados pontos. Cada um desses pontos de intersecção recebeu uma letra (A,B,C,D,E,F).
Dessa forma, teremos vários segmentos de retas formados: AB, BC, AC e DE, EF, DF, eles são partes da reta com tamanhos bem definidos, tendo começo e fim em dois dos pontos.
O teorema nos confirma que esses segmentos são todos proporcionais, ou seja, as razões (divisões) feitas entre eles resulta em um número igual. Para entender melhor sobre razão e proporção, consulte nosso artigo sobre Escala!
Isso significa que é possível deduzir uma igualdade numérica quando relacionarmos esses segmentos. Veremos essa fórmula depois de conhecer a origem dessa ideia!
Onde surgiu o Teorema de Tales e para quê ele serve?
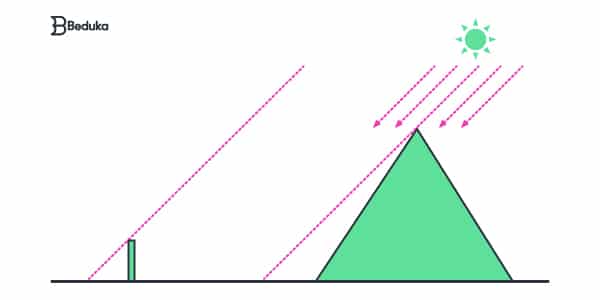
O teorema recebe o nome daquele que o criou : Tales de Mileto. Ele era um filósofo, astrônomo e matemático que vivia na Grécia, na cidade de Mileto, muito antes de Sócrates, Aristóteles ou Platão surgirem.
Dizem que o experimento de Tales foi realizado por meio da observação da sombra da pirâmide. Ele colocou também um palito de medida conhecida e comparou com sua sombra. A partir disso, ele conseguiu calcular a altura da pirâmide Quéops, no Egito, pois os raios solares batiam na pirâmide e no palito com o mesmo grau de incidência!
Com sua teoria, Tales contribuiu para o avanço dos estudos de razão, proporção, geometria e até trigonometria. Até hoje, seus princípios norteiam os cálculos de distâncias das engenharias, da física, e geometria na matemática.
Como se resolve o Teorema de Tales? Fórmula e exemplo
Agora que você já entendeu os termos técnicos, o que diz a teoria e de onde ela surgiu, vamos resumir a ideia de forma bem simples para enxergar a fórmula!
- Resumindo: quando houver duas ou mais retas paralelas “cortadas” por duas ou mais transversais, os segmentos gerados serão proporcionais.
Ser proporcional significa ter a mesma razão e, na matemática, razão indica uma operação de divisão. Por isso, podemos montar a seguinte fórmula:
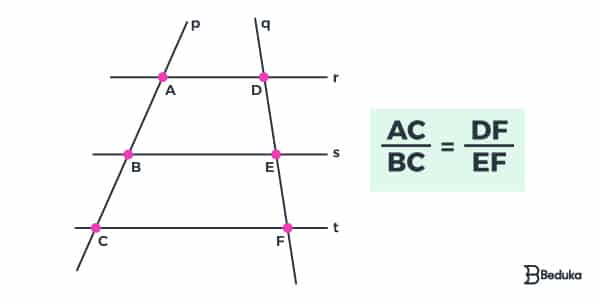
Agora vamos ver um exemplo com números para entender como isso nos auxilia!
- Sabe-se que a escala de temperatura Celsius possui o ponto de ebulição (TE) valendo 100°C e o de fusão (TF) valendo 0°C. Já a escala de temperatura Fahrenheit tem uma TE = 212°F e um TF = 32°F. Descubra a quantos graus F° equivale a temperatura 75°C.
Solução:
Se você não se lembrar da fórmula de conversão de temperaturas, não desespere! Basta usar o Teorema de Tales para identificar a proporção que existe entre as escalas e descobrir o que a pergunta pede.
Para isso, precisamos fazer o esquema dessa forma:
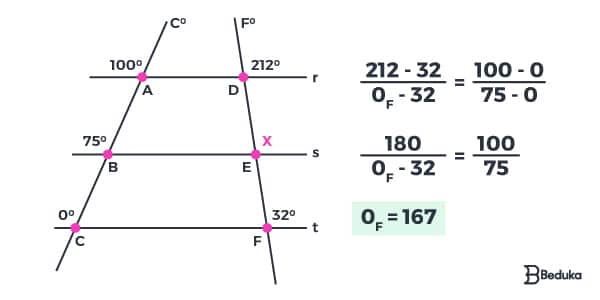
Assim, cada reta transversal será onde colocaremos as temperaturas daquela escala. Como o Teorema nos diz que “AC / BC = DF / EF”, precisamos fazer a subtração dos números para encontrarmos os valores isolados de cada segmento.
Depois, é só jogar na relação e resolver normalmente!
Teorema de Tales no triângulo
Se o teorema de Tales trata de proporção e razão, fica muito fácil de aplicá-lo nos triângulos quando falamos na matéria de Semelhança de triângulos!
Esse teorema pode ser utilizado quando falamos em bissetriz interna do triângulo ou quando traçamos uma reta paralela à base do triângulo. Veja:
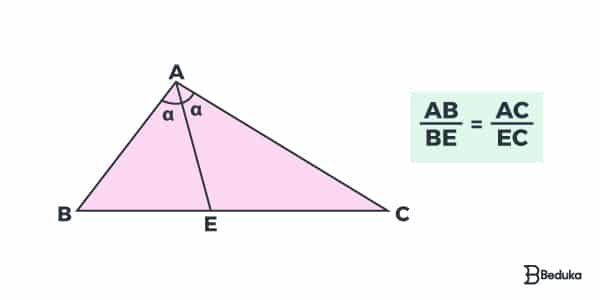
Na imagem, observe que o segmento AD é a bissetriz do triângulo ABC, visto que ele divide o ângulo  em duas partes iguais. Por isso, de acordo com o teorema, o segmento de reta AD divide o lado oposto (BC) em dois segmentos proporcionais aos lados adjacentes (AB e AC) Por isso, podemos escrever aquelas razões.
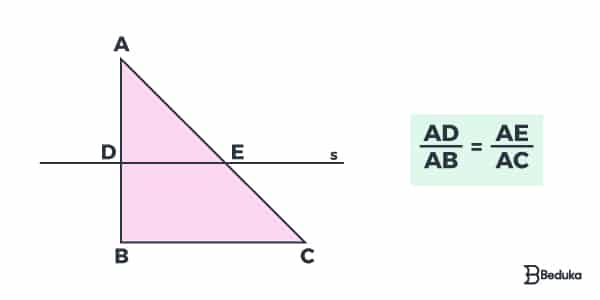
Já na segunda imagem, temos uma estrutura bem semelhante à do Teorema de Tales, bastando aplicar os conceitos e armar a fórmula.
Esse Teorema é muito útil quando nos foram dadas algumas medidas do triângulo e outras faltam, então precisamos de achar! Guarde essa matéria para usar na geometria! Ele também nos permite observar que ambos os triângulos (ABC e ADE) são semelhantes!
Gostou do nosso artigo sobre Teorema de Tales? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!







