Resumo completo de Geometria Plana: dos conceitos às fórmulas!

As figuras 2D, que possuem dimensões de largura e altura, são estudadas pela Geometria Plana. São as que representamos numa folha de papel e no plano cartesiano, como os quadrados, círculos, triângulos, etc. Também há as medidas de área e perímetro que podemos calcular… Saiba como!

Neste artigo sobre Geometria Plana, você encontrará todos os temas abaixo. Clique em um deles para ir direto ao assunto:

1. O que é Geometria Plana e qual é a sua importância?
2. Conceitos básicos: Ponto, Reta e Plano.
3. O que são ângulos?
4. Definição e classificação das Figuras Planas (Polígonos).
5. Triângulos: definição, tipos e elementos.
6. Quadriláteros: definição, tipos e elementos.
7. Pentágonos e Hexágonos: definição, tipos e elementos.
8. Circunferência: definição e elementos.
9. Área e Perímetro: definições e fórmulas de cada figura!

• Estudando para as provas? Conheça O melhor Simulado Enem do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!

O que é Geometria Plana?

A geometria plana é a área da matemática que estuda as figuras de duas dimensões: altura e largura. É como uma folha do caderno, só possui uma superfície!

Estamos falando das formas que podem ser representadas no plano cartesiano. Provavelmente, você já ouviu falar delas: retângulos, quadrados, círculos, triângulos, etc. 

É nessa matéria que estudamos os conceitos, posição e estrutura das formas. Também entendemos os conceitos básicos de ponto, reta, plano e ângulo.

Por fim, veremos como calcular altura, área e perímetro. Você sabe o que é cada uma dessas coisas? Se não, nós te mostramos o conceito, a fórmula e o exemplo!

A geometria plana também pode ser chamada de euclidiana, pois foi Euclides de Alexandria, geômetra grego, que organizou e desenvolveu esses estudos pela primeira vez. Então, ele é conhecido como “pai da geometria”.

• Já deu pra ter uma noção do que vamos estudar? Então vem com a gente!

Qual a importância da geometria plana nos dias de hoje?

A Geometria é essencial para a vida humana, pois começou a ser desenvolvida lá na Grécia Antiga e foi usada como base para quase tudo o que veio depois! 

Ela foi a base para o aprofundamento na matemática, o surgimento de outras geometrias (espacial e analítica), os avanços na arquitetura e o desenvolvimento da física!

Inclusive, está mais presente no nosso cotidiano do que podemos imaginar. Todos os móveis da casa precisaram da geometria para serem feitos. Quando organizamos nosso quarto, também usamos essa matemática!

Outro ponto importante é que cria em nós o raciocínio visual, a percepção de posição e rotação. Isso significa que nos ajuda a ler um mapa, o gps, etc.

Por fim, podemos dizer que ela é uma das matérias preferidas do Enem e dos vestibulares. Portanto, os alunos devem se debruçar sobre ela!

• Você é uma daquelas pessoas que tem fome de conhecimento? Então siga o Beduka no Instagram para conteúdos diários.

Quais os principais conceitos da geometria plana?

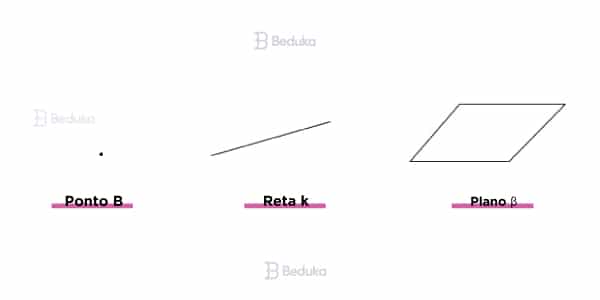
Como a geometria plana estuda as figuras planas, precisamos começar com os conceitos básicos que formam essas figuras: ponto, reta e plano.

Depois de entendê-los, podemos desenvolver os outros: ângulos, áreas, perímetros, etc.

Vamos conhecer cada um deles:

O que é um Ponto?

Os pontos não possuem uma definição. Então, nós só podemos falar sobre suas características, propriedades e utilidades!

Isso acontece porque eles são adimensionais, ou seja, não possuem dimensão. Assim, não podemos medir sua altura, comprimento ou largura.

Como consequência, a nossa maneira de representá-lo visualmente é fazer, literalmente, um pontinho no papel. Por fim, dizemos que os pontos são “aquilo que não tem partes”. Não podemos dividi-lo, ele é inteiro.

O “nome” de cada ponto, que vai diferenciar um do outro, é dado por uma letra maiúscula qualquer.

O que é uma Reta?

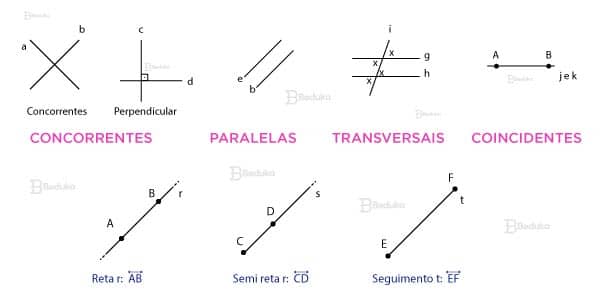
Por definição, uma reta é formada por infinitos pontos seguidos. Ela tem uma dimensão, ou seja, é uma “linha” com comprimento e sem largura. 

Ela costuma ser representada por uma letra minúscula. 

É importante definir que é preciso no mínimo dois pontos para traçar uma reta. Assim, a reta é infinita, não tem começo ou fim, embora nós só representemos uma parte.

Dizemos que há apenas uma reta que passa por dois pontos específicos. Mas, por um ponto qualquer e sozinho, podem passar infinitas retas porque são várias as possibilidades de ele se agrupar com outro ponto!

As retas podem aparecer em 3 posições: horizontal, vertical ou inclinada. 

Posição relativa entre retas

Quando estamos analisando diferentes retas ao mesmo tempo, dependendo da forma que elas se cruzam, podemos dar nomes a esses fenômenos:

• Retas paralelas: quando elas não possuem nenhum ponto em comum, estão perfeitamente alinhadas lado a lado. O símbolo usado para representar é: c // b , ou seja, a reta c é paralela a b.
• Retas concorrentes: quando as retas possuem um único ponto em comum, ou seja, se cruzam em um único lugar. Dependendo do ângulo que formam quando se cruzam, ainda podem ser classificadas em perpendiculares ou transversais.
• Retas coincidentes: são retas que estão sobrepostas, ou seja, possuem todos os  pontos em comum. Nesse caso, elas são iguais.

Posição relativa entre retas e pontos

Quando estamos analisando os pontos ao redor de uma reta, podemos dar nomes a esses fenômenos dependendo da forma que se relacionam:

• Pontos pertencentes: o ponto está localizado sobre a reta ou é um dos que formam a reta.
• Pontos que não pertencem: estão ao redor da reta, mas a reta não passa por eles.

O que é um Segmento de Reta?

O segmento de reta é definido como uma parte da reta. Isso significa que pegamos uma parte da reta (infinita) e delimitamos um segmento (finito). Por isso, o segmento de reta tem início e fim.

O que é uma Semirreta?

O conceito de semirreta surge quando queremos pegar um único ponto da reta como extremidade, mas analisamos tudo o que vem depois. Portanto, uma ponta é delimitada e a outra é infinita!

O que é um Plano?

Um plano é uma região que abrange infinitos pontos e infinitas retas. Ele possui duas dimensões, ou seja, tem comprimento e largura. Geralmente a região que o plano ocupa é representada por letras gregas

O plano que utilizamos aqui é formado pelo eixo das coordenadas e das abscissas, e conseguimos localizar e medir coisas porque está sobre uma reta numérica. É essencial saber sobre o plano cartesiano antes de continuarmos!

O que são Ângulos?

Você acabou de conhecer semirretas, retas e segmentos de reta, e também viu que elas podem se cruzar. Quando isso acontece, é possível determinar a inclinação que as retas formam entre si.

Essa região, que está entre duas semirretas, é chamada de ângulo. Ele é medido em graus e, por definição, essa medida vai de 0° a 360°. 

• Para entender isso, imagine um relógio:

Quando dois ponteiros (segmentos de reta) estão exatamente um sobre o outro, há 0°. Quando um dos ponteiros está parado e o outro dá uma volta completa até chegar a sua posição inicial, ele rodou 360°.

Como os ângulos podem ser classificados?

• Agudo: se sua medida for menor que 90º;
• Reto: se sua medida for igual a 90º;
• Obtuso: se sua medida for maior que 90º e menor que 180º;
• Raso: se sua medida for igual a 180º.

É importante saber que, na geometria, “congruente” significa “igual”. No caso dos ângulos, eles são congruentes se todos os seus elementos coincidem. Isso será a prova de que eles possuem valores iguais.

Para saber se dois ângulos são congruentes, é preciso entender as propriedades geométricas dos ângulos!

O que é uma figura plana? (Polígonos)

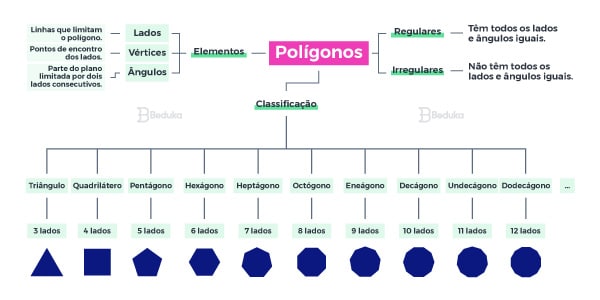
Uma figura plana é uma região fechada formada por segmentos de reta. Note que é preciso no mínimo 3 segmentos para que se forme uma região fechada.

Quando já temos uma figura formada, deixamos de falar “segmentos de reta” e chamamos simplesmente de lados.

Assim, os polígonos são figuras planas de 3 ou mais lados. Seus segmentos de retas não se cruzam, elas apenas encostam suas extremidades e acabam formando ângulos!

Assim, seus elementos básicos são:

• Lado: os segmentos de reta que contornam e fecham a figura.
• Vértice: pontos de encontro que ligam os lados.
• Ângulos: áreas de inclinação entre os lados, ao lado dos vértices.

Formas de classificar os polígonos

Dependendo da quantidade de lados, podemos dar nomes aos polígonos.

Eles também podem ser classificados em regulares ou irregulares, conforme a presença ou ausência de simetria. 

Por fim, podem ser:

• Côncavos: lados que formam uma “área para dentro”. Se traçamos retas entre seus vértices, veremos que algumas reta não passam pela figura
• Convexos; todas as retas traçadas entre os vértices são parte da figura.

Tudo isso é mostrado na imagem acima!

Existem alguns tipos de polígonos que são MUITO cobrados nas provas.

Vamos conhecê-los:

O que são Triângulos?

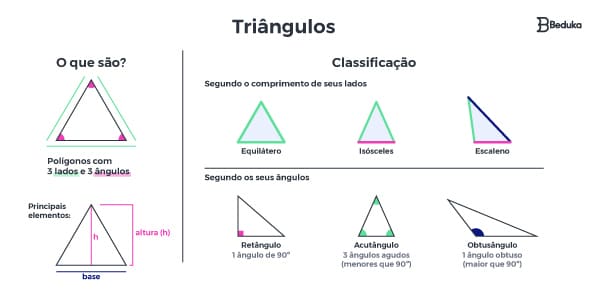
Os triângulos são os polígonos que possuem 3 lados. Como consequência, só existem 3 ângulos e por isso receberam esse nome.

Os matemáticos já comprovaram que a soma dos ângulos internos de um triângulos é sempre 180°. Guarde essa relação!

Classificação de triângulos

Além do que já foi dito, podemos classificar os triângulos dependendo do tipo de ângulo que ele é formado e da congruência entre seus lados.

Veja:

Quanto aos ângulos

• Retângulo: se tiver 1 ângulo valendo 90° (reto)
• Acutângulo: se apresentar ao menos 3 ângulos menores de 90° (agudo)
• Obtusângulo: se tiver 1 ângulo maior que 90° (obtuso)

Quanto aos lados

• Equilátero: possui todos os lados congruentes e, por consequência, todos os ângulos também serão iguais. Como o valor total é 180°, se dividirmos por 3, sabemos que cada um de seus ângulos sempre vale 60°.
• Isósceles: possui 2 lados congruentes. Por consequência, haverá 2 ângulos congruentes, os que são formados entre os lados iguais e a base.
• Escaleno: não possui nenhum lado igual. Isso não nos dá propriedades de ângulo.

Ao final do artigo, falaremos da fórmula da área, mas já te sugerimos aprender sobre:

• Relações métricas nos triângulos retângulos.
• Regras de semelhança de triângulos .
• Como calcular a altura de um triângulo equilátero.

O que são Quadriláteros?

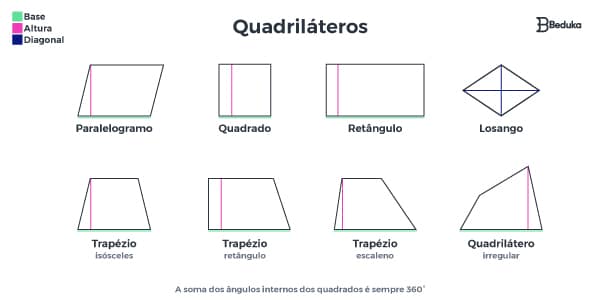
Os quadriláteros são os polígonos que possuem 4 lados, por isso receberam esse nome! Como consequência, existem 4 ângulos na figura, mas uma diversidade de tipos muito maior!

Os matemáticos já comprovaram que a soma dos ângulos internos dos quadriláteros é sempre 360°. Guarde essa relação!

Classificação de Quadriláteros

Além disso, podemos classificar os quadriláteros dependendo do tipo de ângulo, do paralelismo, da congruência de lados e outros fatores.

Os quadriláteros mais famosos são:

• Trapézios
• Paralelogramos
• Retângulos
• Losangos
• Quadrados

Você sabe qual a relação entre eles? Sabia que o quadrado é um tipo de losango? Sabe as fórmulas e propriedades de cada figura?

Então corre pra ver o nosso artigo sobre quadriláteros notáveis!

Polígonos regulares com 5 ou mais lados

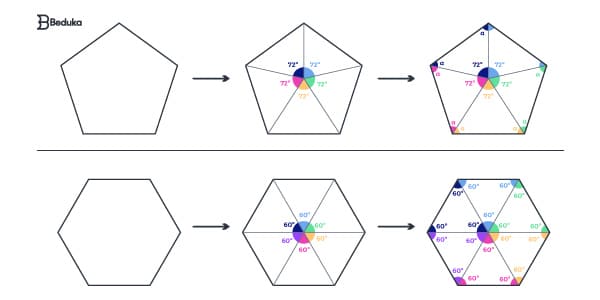
Os polígonos com 5 lados são chamados de pentágonos e os de 6 lados são chamados de hexágonos. Você pode até ficar com medo deles e dos próximos, por pensar que são lados demais!

Nós vamos te ensinar um macete: 

• Todos os polígonos regulares de 5 ou mais lados podem ser decompostos em triângulos ou quadriláteros! 

É isso mesmo! 

O pentágono pode ser dividido em 5 triângulos e o hexágono em 6. E mais: observe que esses triângulos sempre serão equiláteros ou isósceles!

Se você aprender a calcular a área de um triângulo, já saberá a de qualquer polígono regular com 5 ou mais lados. Basta dividir a figura, calcular a área de uma parte e multiplicar pela quantidade de partes totais.

Assim, a nossa vida fica muito mais fácil!

O que é uma Circunferência?

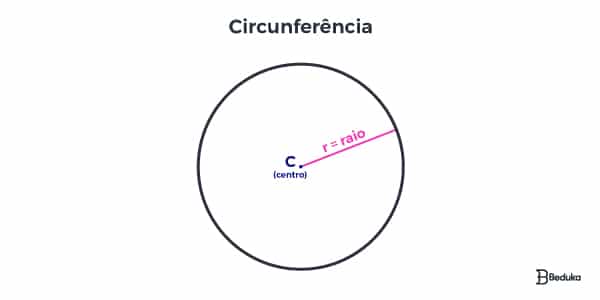
A circunferência é uma figura plana que não é um polígono! Ela é composta por linhas que fazem curva, não por retas ou segmentos.

Sendo assim, a circunferência é formada por todos os pontos que estão a uma mesma distância de um ponto central. Essa distância é chamada de raio (r).

Então, a circunferência é o contorno que delimita o círculo. O círculo é a região que fica limitada pela circunferência.

Por causa disso, ela tem fórmulas próprias para sua área e perímetro! (Veremos ao final do artigo).

Como calcular Área e Perímetro?

Em cada tipo de geometria, usamos conceitos próprios de acordo com a quantidade de dimensões.

Perímetro e área são os que podemos calcular na geometria plana e os usamos para medir elementos da figura. Para encontrar esses valores, é importante analisar o formato da figura em questão.

Você pode acessar o artigo Área, Perímetro e Volume para saber com detalhes. 

Agora, veja os conceitos:

• Área (A): medida da superfície de uma figura. 

Podemos dizer que é o preenchimento de uma figura plana. É como se você quisesse pintar uma folha inteira e calculasse quanto de tinta precisaria para cobrir tudo! 

• Perímetro (2P): medida do contorno de uma figura.

Para enxergar o que estamos dizendo, basta que você se imagine pegando um barbante e contornando um caderno. Depois de marcar até onde foi com o barbante, você desenrola ele e mede na régua.

O valor encontrado é o perímetro! Já o semiperímetro (P) é o valor que representa a metade do perímetro.

Como calcular a área?

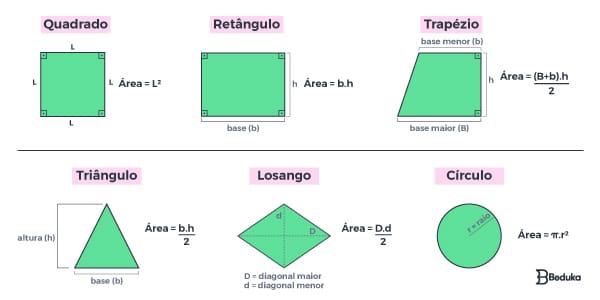
Para calcular a área (A) de uma figura, o comum é multiplicar o valor da base (b) pela altura (h). Mas podem haver algumas variações dependendo do formato.

• Retângulo: segue o raciocínio descrito acima, então a fórmula é:

A (retângulo) = b . h 

• Quadrado: a base e altura tem o mesmo valor dos lados (l), então podemos escrever:

A (quadrado) = l²

• Trapézios: podem ser divididos em triângulos e retângulos, então basta guardar essas duas fórmulas, calcular e somar. Porém, existe uma fórmula própria dos trapézios que envolve a base maior (B) e base menor (b):

A (trapézio) = (B + b) h / 2

• Losango: também pode ser dividido em triângulos, então basta calcular eles e somar. Porém, existe uma fórmula própria para losangos com base em sua diagonal maior (D) e diagonal menor (d):

 A = D . d / 2

• Triângulos: também é dada pela multiplicação de área por altura, mas o valor é dividido na metade porque o triângulo vai “afunilando”:

A (triângulo) = b . h / 2

ou

A (t. equilátero) = √3 . l² / 4)

• Circunferência: a fórmula é completamente diferente, pois envolve o raio (r) e o número pi (π, aproximadamente 3,14):

A (círculo) = π.r²

Como calcular o Perímetro?

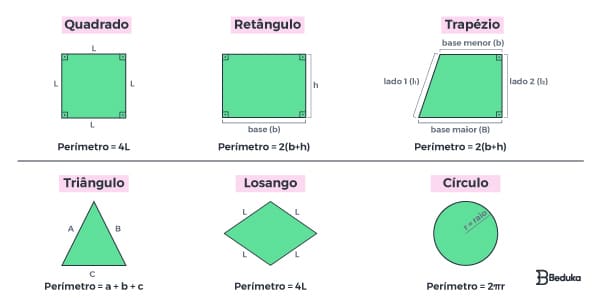
Se o perímetro (2P) é o contorno da figura, podemos dizer que seu valor é encontrado quando se soma os lados de uma figura plana. 

• Portanto, dizemos que:

2P (retângulo) = 2b + 2h

2P (quadrado) = 4l

2P (triângulo escaleno) = a + b + c

2P (t. isósceles) = a + 2b

2P (t. equilátero) = 3l

E assim por diante…

• Circunferência: para as circunferências há uma fórmula específica:

C = 2.π.r

Gostou do nosso artigo sobre Geometria Plana? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet.