Tudo sobre os quadriláteros notáveis!

Os quadriláteros notáveis são polígonos formados por 4 lados. Essas figuras planas são classificadas conforme o número de lados paralelos, podendo ser trapézios ou paralelogramos. Dentre eles, podemos citar os quadrados, losangos e retângulos!

Neste artigo sobre quadriláteros notáveis, você encontrará:

1. O que são quadriláteros notáveis e seus elementos
2. Como podem ser agrupados e quais as suas propriedades
3. Tipos de Trapézios e Paralelogramos
4. Quadrado, losango e retângulos
5. Área e propriedades de lados e ângulos

• Estudando para as provas? Conheça o melhor Simulado gratuito do Brasil, que pode ser personalizado com as matérias que você mais precisa!

O que são quadriláteros notáveis?

De acordo com a geometria plana, os quadriláteros são polígonos que possuem 4 lados. Essas figuras geométricas são planas porque pertencem ao plano cartesiano, logo, elas têm apenas 2 dimensões (altura e largura).

Ser um polígono significa ser formado por segmentos de retas (linhas com início e fim) que não se cruzam. Elas apenas encostam suas extremidades e acabam formando uma figura fechada. No caso dos quadriláteros, há 4 segmentos de retas.

Quando usamos o termo “notável” na matemática, significa que é algo importante e principal. Existem muitas figuras com quatro lados, mas há aquelas que utilizamos mais no dia a dia e para estudar na matemática.

Portanto, os quadriláteros notáveis são os polígonos de 4 lados mais importantes de se estudar!

Quais são os quadriláteros notáveis?

Os quadriláteros notáveis são 5:

• Trapézios
• Paralelogramos
• Retângulos
• Losangos
• Quadrados

Mais a frente iremos estudar cada um deles individualmente, mas antes vamos conhecer os seus elementos em comum:

Elementos de um quadrilátero

• Lados: são os segmentos de reta que formam o contorno do quadrilátero. Costumamos dar nomes genéricos para eles, como “lado a”. Mas a forma matemática de representá-los é escrever os vértices das suas extremidades juntos, com um traço em cima.
• Vértices: são os pontos que marcam o encontro de dois lados. Essas quinas também recebem nomes genéricos, como “vértice A”.
• Ângulos internos: são os ângulos que estão do lado de dentro do polígono, então são formados por dois lados seguidos do quadrilátero.
• Ângulos externos: são ângulos que estão do lado de fora do polígono, então são  formados pelo prolongamento de um lado do quadrilátero. Um ângulo externo é suplementar ao interno adjacente. Isso significa que se somarmos o externo e o interno ao seu lado, eles resultam em 180°.
• Diagonais: são segmentos de reta imaginários que passam por dentro do polígono, não são lados. Suas extremidades são 2 vértices não consecutivos, por ser um quadrilátero, podemos dizer que são vértices opostos.

Como os quadriláteros podem ser agrupados?

Você já deve ter ouvido falar nos quadriláteros citados acima, não é mesmo? O que talvez seja novidade para você é:

Os quadriláteros podem ser agrupados em três grandes conjuntos, de acordo com a presença e quantidade de paralelismo:

• Trapézios: possuem ao menos um par de lados paralelos.
• Paralelogramos: possuem ao menos dois pares de lados paralelos.
• Outros: não possuem nenhum par de lados paralelos.

Parece estranho, mas é isso mesmo! Um trapézio é uma categoria de quadriláteros, não uma figura em si. Existem diversos tipos de trapézios que são figuras próprias. A mesma coisa acontece com os paralelogramos.

O paralelismo acontece quando temos dois lados paralelos entre si, ou seja, duas retas que são perfeitamente opostas. Assim, elas nunca se encontrarão, nem mesmo se prolongarmos sua extensão. Resumindo, são lados que não tem nenhum ponto em comum.

Para você entender melhor o que estamos dizendo, veja a representação no diagrama de Venn:

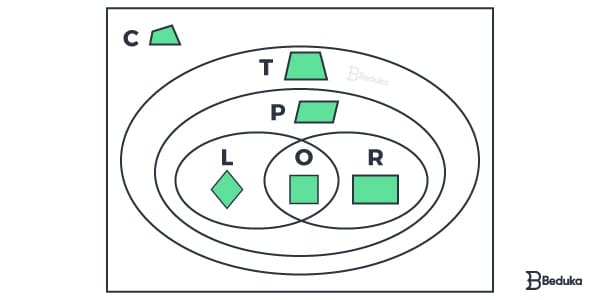
No qual:

C: quadriláteros

T: trapézios

P: paralelogramos

R: retângulos

L: losangos

Q: quadrados

Quais são as propriedades dos quadriláteros?

Como qualquer polígono, todos os quadriláteros também possuem as características e propriedades básicas: 

• Possuem diagonais e, no caso dos quadriláteros, são apenas 2
• A soma dos seus ângulos internos é sempre igual a 360°

Não se engane, essas não são as únicas propriedades que um quadrilátero pode ter. Citamos acima o comum de todos os polígonos, portanto, são as coisas gerais. 

Assim, cada tipo de quadrilátero notável tem suas propriedades únicas além dessas. Vamos conhecê-las!

Propriedades dos Trapézios

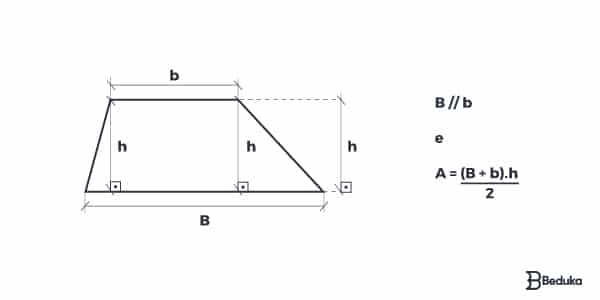
Os Trapézios são quadriláteros que possuem ao menos 1 par de lados paralelos. Existem três tipos de trapézios que variam conforme a simetria e os ângulos, cada um com suas propriedades específicas:

• Trapézio Escaleno
• Trapézio Isósceles
• Trapézio Retângulo

A área de qualquer trapézio é sempre dada pela soma das bases multiplicada pela altura dividida por 2. Assim:

A = (B+b).h/2

Sendo

• b: base menor (paralela menor)
• B: base maior (paralela maior)
• h: altura (fora ou dentro, o importante é fazer ângulo reto com um dos lados paralelos)

Se você não decorou a fórmula, basta dividir a figura do trapézio em triângulos e retângulos, assim você faz a área de cada figura individualmente e soma ao final!

Por fim, para encontrar a base média de um trapézio, basta fazer (b +B) / 2. Ela será paralela aos lados paralelos, localizada bem no meio da figura. Seus vértices são os pontos médios dos lados não paralelos.

Trapézio Escaleno

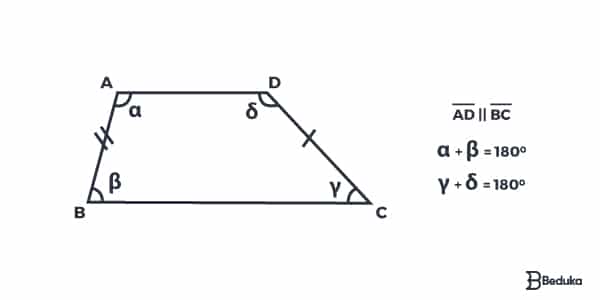
É o trapézio em que os lados não paralelos são diferentes entre si, ou seja, não tem a mesma medida. Representamos isso com a presença de risquinhos, como você observa na imagem. Um risco significa ter uma medida e dois riscos significa ter outra medida.

Observe que os ângulos opostos são suplementares, ou seja, quando somados resultam em 180°.

Trapézio isósceles

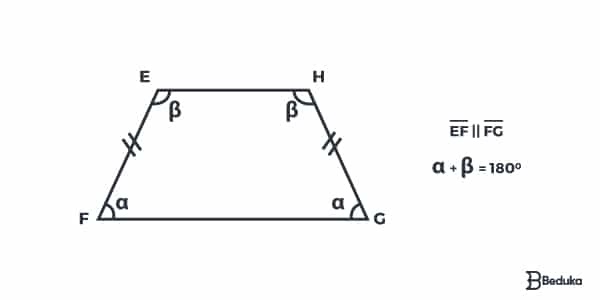
É o trapézio em que os lados não paralelos são congruentes, ou seja, são iguais. Representamos isso com a presença dos mesmos risquinhos em cima desses lados.

É interessante notar que, os lados não paralelos terem a mesma medida, faz com que os ângulos também sejam congruentes! Assim, embora existam 4 ângulos, há apenas 2 valores diferentes.

Novamente, temos que os ângulos opostos são suplementares.

Trapézio retângulo

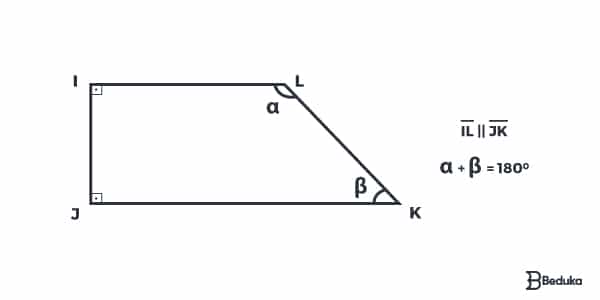
É o trapézio em que um dos lados não paralelos é perpendicular aos lados paralelos. Isso significa que haverá, necessariamente, a formação de ângulos retos (90°). Como temos uma reta perpendicular a duas retas paralelas, forma-se 2 ângulos retos.

Este é o único trapézio em que os ângulos opostos não são suplementares. São os ângulos internos e seguidos que formam 180°.

Propriedades dos Paralelogramos

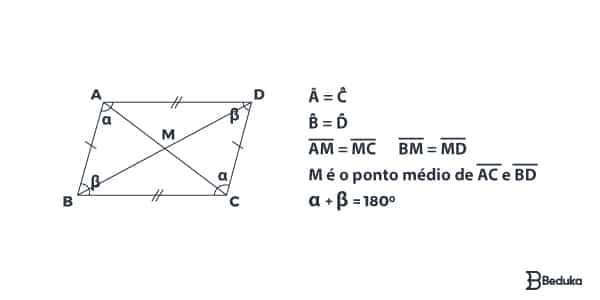
Os Paralelogramos são quadriláteros que possuem ao menos 2 pares de lados paralelos. Como consequência de ser um quadrilátero e estar nestas condições, todos os seus lados são paralelos. Então, podemos chamá-los de paralelogramos.

Existem três tipos famosos de paralelogramos:

• Retângulos
• Losangos
• Quadrados

Todos os paralelogramos acima apresentam as seguintes propriedades específicas:

• Ângulos opostos são congruentes.
• Possui duas diagonais que se cruzam em um ponto central. Este é o ponto médio, que divide cada diagonal em 2 segmentos congruentes.
• 2 ângulos internos e consecutivos são suplementares.

Adiante veremos as propriedades individuais de cada tipo de paralelogramo, que se somam a essas.

ATENÇÃO: pela própria definição, concluímos que todo paralelogramo é um trapézio, pois realmente possui ao menos 1 par de lados paralelos. Mas nem todo trapézio é um paralelogramo, porque pode ter apenas 1 par e não 2.

Retângulos

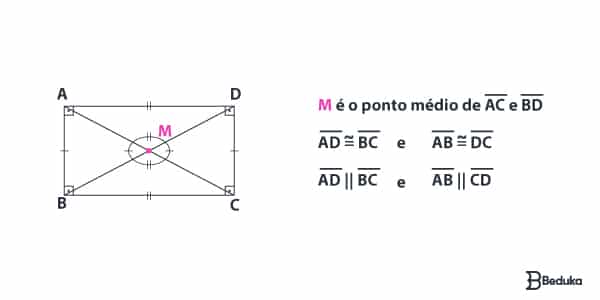
Os retângulos são paralelogramos que possuem todos os ângulos internos retos, ou seja, valendo 90°. 

Como o retângulo é um polígono quadrilátero, ele “já vem” com as propriedades mencionadas anteriormente. 

O que tem de específico (só dele) é:

• Os lados que formam um par de paralelos são congruentes (mesma medida);
• Os ângulos formados entre as diagonais são: 2 pares iguais, mas diferentes entre si (regra dos ângulos opostos pelo vértice);
• A divisão da figura por suas diagonais forma 2 pares de triângulos iguais, todos do tipo isósceles.

A área de um retângulo é dada pelo lado vezes a altura:

 A = l . h

Se usarmos a figura acima como exemplo, seria: lado BC . lado AB

Losangos

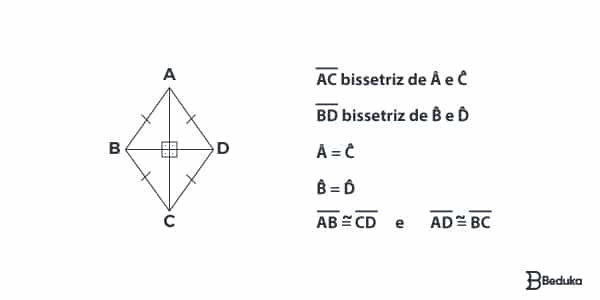
Os losangos são paralelogramos que possuem todos os lados congruentes, ou seja, todos os lados têm a mesma medida. Observe que os risquinhos sobre os lados indicam isso!

Como ele é um polígono quadrilátero, “já vem” com as propriedades mencionadas anteriormente. 

O que tem de específico é:

• As diagonais são bissetrizes dos ângulos nos vértices de qual partem (dividem ele no meio exato, formando duas metades iguais);
• Os ângulos formados entre as diagonais são todos retos, as diagonais são perpendiculares entre si;
• A divisão da figura pelas diagonais forma 4 triângulos retângulos iguais.

A área de um losango é dada pela diagonal maior vezes a menor, dividido por 2. Assim:

 A = D . d / 2

Se usarmos a figura acima como exemplo, seria: diagonal AC. diagonal BD dividido por 2.

Quadrados

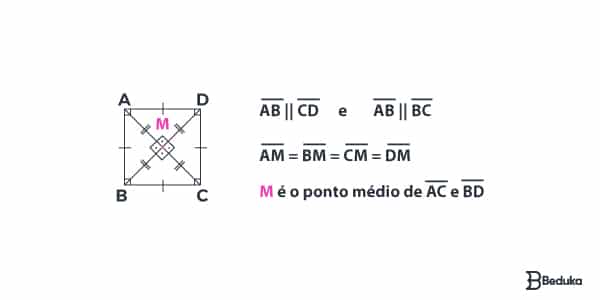
Os quadrados são paralelogramos que possuem todos os lados congruentes e todos os ângulos retos. Isso significa que ele é um caso particular, porque mistura as características do losango + retângulo. 

Como ele é um polígono quadrilátero, “já vem” com as propriedades mencionadas anteriormente, bem como as do losango e as do retângulo.

O que tem de específico é:

• O ponto médio de cada diagonal divide as 2 diagonais em 4 segmentos congruentes;
• A divisão da figura pelas diagonais forma 4 triângulos isósceles iguais.

A área de um quadrado é calculada com a mesma fórmula do retângulo (lado vezes altura). Como o quadrado é todo igual, lado e altura possuem o mesmo valor. 

Quando multiplicamos um número por ele mesmo, estamos fazendo o seu quadrado. Logo, a fórmula pode ser escrita como:

 A = l²

Se usarmos a figura acima como exemplo, seria: lado AB².

Gostou do nosso artigo sobre quadriláteros notáveis? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!