As relações métricas no triângulo retângulo são regras em forma de equações que podem ser encontradas em qualquer triângulo que tenha um ângulo de 90°. Elas estabelecem padrões entre as medidas e podem nos ajudar a achar alguma medida faltante. São 5 as relações mais importantes!
Neste artigo sobre Relações métricas no Triângulo Retângulo, você encontrará:
- O que são Relações métricas?
- O que é um Triângulo Retângulo e quais seus elementos?
- Semelhança de triângulos
- Como resolver Relações métricas no Triângulo Retângulo? Exemplos
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que são Relações métricas? Para que servem?
As relações métricas são leis que existem dentro de triângulos, representadas por uma equação. Você já deve ter ouvido falar que a soma dos ângulos internos de todo triângulo é 180°. Da mesma forma, os triângulos retângulos possuem algumas propriedades que são só deles, e são descritas por uma fórmula matemática.
Saber essas relações é importante para resolver exercícios da Geometria Plana, porque você pode se deparar com uma questão em que há medidas das partes de um triângulo retângulo que estão faltando. Para descobrí-las, você precisa jogar os dados na equação e resolver até achar o resultado!
O que é um Triângulo Retângulo e quais são seus elementos?
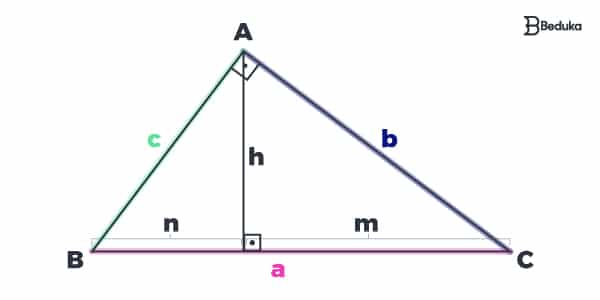
Antes de lidarmos com as relações, precisamos lembrar o que caracteriza um triângulo retângulo e quais podem ser as partes faltosas. Observe a imagem e leia a legenda:
- Hipotenusa (a): é o maior lado de um triângulo retângulo, sempre oposto ao ângulo de 90º, que é obrigatório existir para que seja considerado retângulo.
- Catetos (c e b): são os outros dois lados restantes.
- Altura (h): todo segmento retilíneo que parte de um ponto e forma um ângulo reto (90°) com um lado. Neste caso, utilizamos a altura relativa à hipotenusa.
- Projeções dos catetos na hipotenusa (m e n): m é a projeção do c e n é a projeção do b.
Agora que você já conhece as partes dos triângulos, saiba que é com elas que iremos trabalhar para descobrir os valores!
Semelhança de triângulos
A última coisa que precisamos para começar a pôr a mão na massa, é relembrar o que é semelhança de triângulos. Você pode conferir o nosso artigo completo no link, mas aqui deixamos apenas um resumo.
Existem três casos que nos permitem descobrir se dois triângulos são semelhantes entre si ou não. Se forem, isso significa que são proporcionais. É por esse motivo que só aplicamos as relações métricas em triângulos semelhantes, isso nos garante que aquelas fórmulas sempre funcionarão em qualquer um dos triângulos envolvidos.
Observe a decomposição de um triângulo retângulo em seus semelhantes, e aplique os casos (LAL, AAA, ALA) para comprovar se são mesmo!
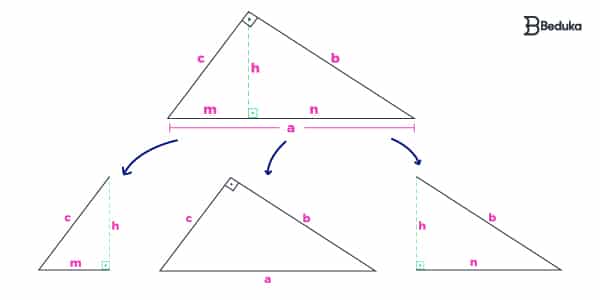
Seguindo a definição “Dois ou mais triângulos são considerados semelhantes quando seus ângulos correspondentes são congruentes e os lados homólogos são proporcionais”, podemos observar que as relações métricas vieram dessas análises!
Vamos conhecê-las logo:
Como resolver Relações métricas no Triângulo Retângulo? Exemplos
Existem 5 relações fundamentais que precisamos ter em mente para estarmos preparados para qualquer questão!
Veja:
Primeira relação métrica: Teorema de Pitágoras!
Se você já conhece o Teorema de Pitágoras pode passar para a próxima, mas saiba que ele é sim a primeira e a mais importante relação métrica!
Vamos entender: a regra/fórmula do Teorema de Pitágoras diz que em todo triângulo retângulo podemos observar a seguinte equação:
- cateto² + cateto² = hipotenusa²
Ou, simplesmente:
- cat² + cat² = hip²
Exemplo:
Qual é a medida da diagonal de um retângulo cujo lado maior mede 60 cm e o lado menor mede 30 cm?
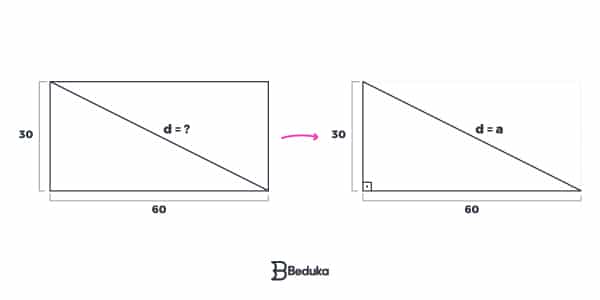
Solução:
A diagonal de um retângulo divide-o em dois triângulos retângulos iguais, sendo que essa diagonal mede exatamente a hipotenusa do triângulo formado.
Como já temos o valor dos catetos, basta aplicar a regra do Teorema de Pitágoras para descobrir quanto vale a hipotenusa/diagonal:
a² = b² + c² ou hip² = cat² + cat²
a² = 30² + 60²
a² = 900 + 3600
a² = 4500
a = √4500
a/d = 67,08 (aproximadamente).
Segunda relação métrica
A segunda relação métrica não tem um nome específico, mas ela diz que: “a hipotenusa do triângulo retângulo é igual à soma das projeções de seus catetos sobre a hipotenusa”. Traduzindo para uma fórmula matemática, temos:
- a = m + n
Exemplo:
Imagine um triângulo ABC com a altura h dividindo a hipotenusa nas projeções m e n. Supondo que os valores das projeções sejam 2 e 4, descubra o valor da hipotenusa do triângulo ABC.
Solução:
Para descobrir quanto vale o lado AB, basta somar m e n, pois no desenho vemos perfeitamente que eles juntos equivalem ao lado da hipotenusa do triângulo geral. Logo:
2 + 4 = 6, então a hipotenusa do triângulo ABC vale 6.
Terceira relação métrica
A terceira relação métrica, como as demais que se seguem, não tem nome. Mas, ela diz: “o quadrado da altura da hipotenusa de um triângulo retângulo é igual ao produto das projeções de seus catetos sobre a hipotenusa”. Em linguagem numérica temos:
- h² = m·n
Exemplo:
Um triângulo ABC possui projeções dos catetos sobre a hipotenusa medindo 100 e 400 centímetros, qual é a sua altura?
Solução:
h² = m·n
h² = 10·40
h² = 40000
h = √40000
h = 200 centímetros.
Quarta relação métrica
Essa relação diz que: “o produto entre a hipotenusa a e a altura relativa à hipotenusa h é exatamente igual ao produto entre catetos b e c”. Traduzindo para as fórmulas, teremos:
- a . h = b . c
Exemplo:
Um triângulo ABC possui altura valendo 5cm , um dos catetos vale 8 e sua hipotenusa vale 10. Descubra quanto vale o outro cateto.
Solução:
a . h = b . c
5 . 10 = 8 . x
50 = 8x
50/8 = x
x = 6,25 cm
Quinta relação métrica
Esta última relação diz que: “o quadrado da medida de um cateto é sempre igual ao produto entre a sua projeção sobre a hipotenusa e a própria hipotenusa”. Traduzindo:
- c² = m . a ou b² = n . a
Exemplo:
Um triângulo ABC possui hipotenusa valendo 10cm. se a projeção do cateto c vale 4cm, descubra quanto vale este cateto.
Solução:
c² = m . a
c² = 4 . 10
c² = 40
c = √40
c = 6,32 cm(aproximadamente)
Gostou do nosso artigo sobre Relações métricas no Triângulo Retângulo? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!







