O Princípio fundamental da contagem (PFC), conhecido como princípio multiplicativo, é um dos tipos de cálculos da Análise Combinatória. Ele aponta que para achar o total de possibilidades de um evento com etapas sucessivas e independentes, devemos multiplicar entre si os números das possibilidades presentes em cada etapa.
Neste artigo sobre o Princípio fundamental da contagem, você encontrará:
- O que é Análise Combinatória
- O que é Princípio Fundamental da Contagem e como calcular
- Para quê serve Fatorial, como utilizar e calcular?
- Exemplos ilustrativos com diagrama!
- Simulado online e gratuito de qualidade é só no Beduka! Você pode até personalizar com as matérias que preferir!
O que é Análise Combinatória
A Análise Combinatória é a área da Matemática que estuda as formas de resolver problemas relacionados à contagem de elementos ou às possibilidades de algo ocorrer.
Por exemplo, se queremos saber de quais modos diferentes podemos organizar pessoas na fila ou qual o número de senhas que podemos formar com 3 letras e 3 números.
Cada questão criará um contexto diferente, com elementos e objetivos distintos. Assim, você deverá saber qual método usar em cada caso!
O que é Princípio Fundamental da Contagem (PFC)
O princípio fundamental da contagem é o primeiro e mais básico método de resolver as questões da Análise Combinatória.
Ele também é conhecido como Princípio Multiplicativo e, como o próprio nome aponta, sua “lei” diz que devemos multiplicar o número de opções que há em cada etapa apresentada.
- De forma mais completa:
“Quando um evento é composto por etapas sucessivas e independentes, sendo as possibilidades da primeira etapa representadas pelo X e as da segunda por Y, o total de possibilidades será dado pelo produto entre X e Y.”
Ainda tem dúvida? Vamos a um exemplo ilustrado para facilitar:
Exemplo
Questão 01
O kit de uma lanchonete é formado por suco, sanduíche e sobremesa. As opções de suco são laranja, morango ou uva; os sanduíches podem ser de frango ou boi e a sobremesa é chocolate ou bala. Quantos kits diferentes um cliente pode montar?
Para resolver essa questão de forma fácil, vamos utilizar um diagrama de árvore:
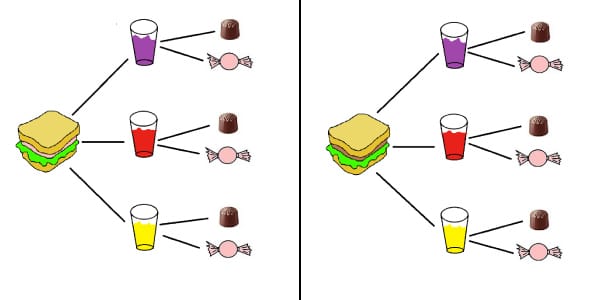
Observe que há duas possibilidades de sanduíche, e cada uma delas possui 3 possibilidades de suco. Por sua vez, cada uma dessas tem sua possibilidade de sobremesa.
Ao todo, enxergamos 12 possibilidades!
- Contudo, nem sempre teremos espaço e tempo para desenhar as possibilidades, então precisamos entender os cálculos ques nos permitem fazer essa análise!
- Por isso existe o Princípio Fundamental da Contagem, veja como seria a resolução utilizando ele:
Foi dito que existem 3 opções de suco, 2 de sanduíche e 2 de sobremesa. Observamos que são 3 etapas independentes entre si e com um número de opções em cada uma. Por tanto, multiplicamos os seguintes fatores:
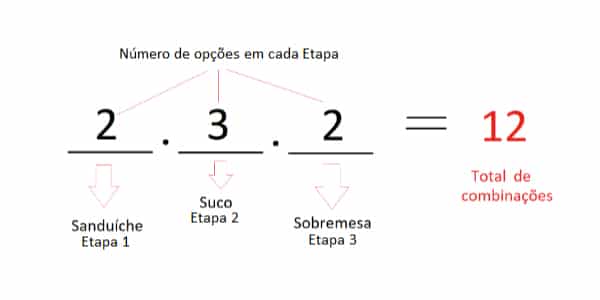
Questão 02
Juninho brincava com um dado e notou que também possuía uma moeda em seu bolso. Como era um garoto muito esperto e amava matemática, decidiu descobrir quantas possibilidades de resultados distintos há ao lançar uma moeda e um dado. Qual foi o número corretamente encontrado por ele?
Ao lançarmos uma moeda e um dado temos as seguintes possibilidades:
Moeda: cara ou coroa (2 possibilidades)
Dado: 1, 2, 3, 4, 5, 6 (6 possibilidades)
Observando o ocorrido, vemos que para cada uma das 2 possibilidades da moeda há outras 6 no dado. Portanto, o evento tem duas etapas com 2 possibilidades na primeira e 6 na segunda.
Fazendo 2 x 6 encontramos o total de 12 possibilidades totais!
Questão 03
O prefeito da Transitolândia deseja criar placas para os automóveis. Elas devem conter placas de exatamente 3 dígitos. Somente os algarismos pares podem ser utilizados e não pode haver repetição de algarismos em uma mesma placa. Quantas possibilidades de placas distintas ele terá?
Os algarismos pares são: 0,2,4,6 e 8 (4 opções) e há 3 dígitos para serem preenchidos.
Como são placas, não existe uma ordem correta para começar ou terminar. Portanto, pode colocar qualquer um dos 4 números na primeira casa. Sobrará 3 números para a segunda casa e 2 para a última, já que não pode haver repetição em uma mesma senha.
Assim, teremos que 5 x 4 x 3 = 60, logo há 60 opções de placas distintas, seguindo essas exigências do prefeito.
ATENÇÃO:
Atente-se para os detalhes dos comandos da questão!
- Se fossem permitidas repetições de números em uma mesma placa, seria um resultado diferente.
- Se fosse dito que o número da placa como um todo deve ser par e pudesse utilizar todos os algarismos de 0 a 9, deveríamos ter o cuidado de colocar primeiro os algarismos pares no último dígito da placa. Assim, garantiríamos a condição que foi dada e calcularíamos as demais possibilidades.
Para quê serve Fatorial, como utilizar e calcular?
O fatorial é uma ferramenta matemática utilizada para simplificar os cálculos matemáticos. Ele é muito utilizado na Análise Combinatória e no PFC!
O seu símbolo é o mesmo que o do sinal de exclamação “!”, e toda vez que aparecer diante de um número, significa que faremos o fatorial dele.
Observe:
- Portanto, consiste em multiplicar o número com o fatorial, por todos os seus antecessores inteiros até chegar ao 1.
Utiliza-se muito o fatorial nos cálculos de anagramas de uma palavra. Lembre-se que anagrama é a quantidade de novas palavras formadas (com ou sem sentido) utilizando as letras de outra palavra.
Exemplo
Se quisermos determinar todos os possíveis anagramas da palavra PEDRA, teremos:
A palavra é formada por 5 letras não repetidas e há 5 espaços para serem preenchidos com uma letra em cada. Portanto, podemos colocar 1 letra qualquer, dentre as 5, no primeiro espaço.
Restará 4 para o segundo, 3 para o terceiro, 2 para o quarto e 1 para o quinto. Dessa forma, se utilizarmos o PFC, teremos: 5 x 4 x 3 x 2 x 1, ou seja, o mesmo valor de 5!
Assim, sabemos que PEDRA possui 120 anagramas!
Gostou do nosso artigo sobre o Princípio Fundamental da Contagem? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!
