Como o próprio nome diz, a função inversa é o inverso de uma função f(x); ou seja, pode ser sinalizada como f(x)-1. Para calcular a sua lei de formação, basta duas etapas: trocar as incógnitas e isolar o y. Leia o resumo, veja os exemplos com explicações detalhadas e, no final, resolva os exercícios de função inversa!
Quer seguir diretamente para alguma parte? Clique em um dos tópicos abaixo:
- O que é uma função inversa? (o que é função, elementos e bijetora).
- Como calcular o inverso de uma função? + exemplo.
- Como é o gráfico de uma função inversa?
- Lista com exercícios de função inversa!
- Gabarito das questões de função inversa.
Quando você terminar os exercícios sobre função inversa, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil!
O que é uma função inversa?
Como aponta o seu próprio nome, a função inversa é o inverso de uma função f(x); ou seja, pode ser sinalizada como f(x)-1.
Isso significa que se uma função tem uma operação de soma na sua lei de formação, a inversa será dada pela subtração. Além disso, para que a inversão seja possível, é preciso que a função seja bijetora.
Ah, você não está lembrado desses nomes todos? Calma!
Nos próximos tópicos, vamos te lembrar o que os nomes específicos significam e depois dar alguns exemplos.
O que é uma função?
As funções matemáticas são expressões que possuem dois lados separados pelo sinal de igual (=) e obedecem uma regra, a lei de formação.
De um lado temos o “f(x)” que representa o valor final da função. Esse valor também pode ser escrito como “y”.
Do outro lado, temos a regra matemática, ou seja, um conjunto de números que rodeiam o valor “x”.
Quando usamos a expressão “em função de”, dá uma ideia de relação entre as coisas. Portanto, ser uma função significa ter dependência, ou seja, o valor da função “f(x)” ou “y” se modifica à medida que modificamos o valor de “x”.
Por isso, devemos resolver as funções pensando nos pares ordenados (x,y) que se adequam àquela regra.
A regra define a “cara” de cada função: como será o seu gráfico e qual a proporção que há entre x e y (se um será o dobro do outro, ou o triplo, ou outra razão).
Quais são os elementos da função?
Toda função pode ser descrita tendo três elementos:
- Domínio (D): conjunto dos valores que podemos colocar em “x”.
- Contradomínio (CD): conjunto de todos os valores possíveis de serem gerados.
- Imagem (I): valores do CD que satisfazem a função, ou seja, são os verdadeiros “y” de cada “x”.
O que é uma função bijetora?
A função Bijetora é aquela em que cada elemento do Domínio possui um único elemento na Imagem (e vice-versa). Isso significa que determinado valor de “x” só pode resultar em “y”, bem como um resultado “y” sempre corresponde ao valor “x”.
Você deve estar se perguntando se existem outros tipos de função, em que isso não aconteça dessa forma. A resposta é sim! São as do tipo Injetora e Sobrejetora.
Aprenda a calcular o inverso de uma função em 2 passos
Para conseguirmos encontrar a lei de formação de uma função inversa, precisamos inverter as incógnitas. Assim, vamos trocar “x por y” e “y por x”.
Depois, precisamos isolar a incógnita “y” no primeiro membro e colocar os demais componentes no segundo. Aí teremos uma nova lei de formação prontinha!
Lembre-se: é importante que a função seja bijetora. Caso contrário, não será possível fazer a inversão de forma correta!
Exemplo
Dada a função f(x) = 2x – 3, calcule a sua inversa.
Resolução:
1° passo: trocar incógnitas:
f(x) = 2x – 3
y = 2x – 3
x = 2y – 3
2° passo: isolar o “y”:
x = 2y – 3
-2y = -3 – x (-1)
2y = 3 + x
y = (3+x) / 2
y = 3/2 + x/2
Simples, não é? Só tome muito cuidado com os sinais e com as operações! Lembre-se também que, quando envolver expoentes, pode ser que você precise usar propriedades logarítmicas ou radiciação.
Como é o gráfico de uma função inversa?
O gráfico de uma função inversa sempre será a inversão do gráfico da função original. Isso significa que ele será simétrico, como se estivesse espelhado.
É bom saber disso porque às vezes pode ser dado apenas o gráfico, não sua lei de formação. Assim, por ele conseguimos analisar se é crescente, decrescente, etc.
- São mais de 200 resumos gratuitos para o ENEM no Instagram do Beduka, aproveite!
Os 10 exercícios de função inversa!
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Obrigado por ter lido até aqui!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1- (Mundo Educação)
Seja f : A → B, tal que f(x) = 5x – 3, uma função inversível, então o valor de f-1(7) é:
a) 0.
b) 1.
c) 2.
d) 3.
e) 4.
Questão 2- (UEL)
Sendo f: R → R+* a função definida por f(x) = 2x, então a expressão que define a função inversa de f é:
a) x².
b) 2/x.
c) log2x.
d) √x.
e) 2-x.
- Você já fez 20% dos exercícios de função inversa. Continue assim!
Questão 3- (FEI)
Se a função real f é definida por f(x) = 1 / (x + 1) para todo x > 0, então f-1(x) é igual a:
a) 1 – x.
b) x + 1.
c) x -1 – 1.
d) x -1 + 1.
e) 1 / (x + 1).
Questão 4- (UFPA)
O gráfico de uma função f(x) = ax + b é uma reta que corta os eixos coordenados nos pontos (2, 0) e (0, -3). O valor de f (f -1(0)) é:
a) 15/2.
b) 0.
c) –10/3.
d) 10/3.
e) –5/2.
Questão 5- (Matemática básica – adaptada)
Seja a função f: R -> R, definida por f(x) = (2x – 1) / 3, calcule f-1(2).
a) 7.
b) 2/7.
c) 5.
d) 7/2.
e) 2.
- Muito bem! Você chegou à metade das questões sobre função inversa. Continue fazendo o restante.
Questão 6- (SEEDUC RJ)
Considere a função de variável real f(x) = (3x + 8) / 2. Qual o valor de f-1(10)?
a) 1 ⁄ 19.
b) 6.
c) 0,25.
d) 4.
e) 19.
Questão 7- (UNEMAT – adaptada)
Seja a função f de R- em R+, definida por f (x) = x² . Qual é a função inversa de f ?
a) f-1(x) = -x².
b) f-1(x) = -x.
c) f-1(x) =x .
d) f-1(x) = 2.
Questão 8- (EEAR)
Seja a função f : R → R definida por f(x) = 4x – 3. Se f-1 é a função inversa de f, então f-1(5) é:
a) 17.
b) 1/17.
c) 2.
d) ½.
- Ufa! Agora só faltam mais dois exercícios sobre função inversa!
Questão 9- (Matematiquês)
A função cujo gráfico está representado na figura 1 a seguir tem inversa.
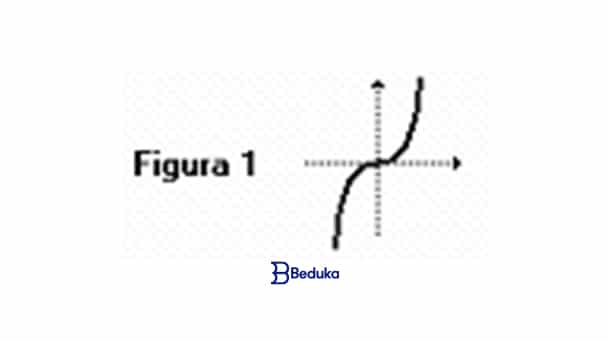
O gráfico de sua inversa é:
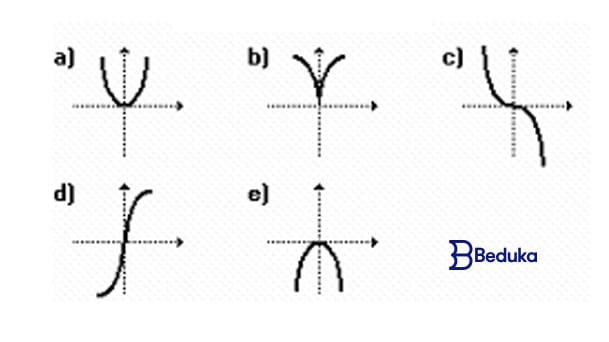
Questão 10- (Brasil Escola)
Se f-1 é a função inversa de f, que vai de R em R, cuja lei de formação f(x) = 2x – 10, o valor numérico de f -1(2) é:
a) 1.
b) 3.
c) 6.
d) -4.
e) -6.
- Parabéns, você fez todas as questões de função inversa. Confira agora o Gabarito:
Gabarito das questões de função inversa
Exercício resolvido da questão 1 –
Alternativa correta: c) 2.
Exercício resolvido da questão 2 –
Alternativa correta: c) log2x.
Exercício resolvido da questão 3 –
Alternativa correta: c) x -1 – 1.
Exercício resolvido da questão 4 –
Alternativa correta: b) 0.
Exercício resolvido da questão 5 –
Alternativa correta: d) 7/2.
Exercício resolvido da questão 6 –
Alternativa correta: d) 4.
Exercício resolvido da questão 7 –
Alternativa correta: b) f-1(x) = -x.
Exercício resolvido da questão 8 –
Alternativa correta: c) 2.
Exercício resolvido da questão 9 –
Resposta correta: c)
Exercício resolvido da questão 10 –
Resposta correta: c) 6.
- Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos exercícios de função inversa? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.





