Tudo o que você precisa para entender Logaritmo e saber usá-lo!

Logaritmo é o nome que se dá à operação matemática utilizada para resolver cálculos relacionados à potenciação, sendo considerado o seu inverso. Nele, buscamos descobrir o valor do expoente que a base deve ter para formar a potência pedida.

Neste artigo sobre Logaritmo você encontrará todos os tópicos abaixo. Clique em um deles para ir diretamente ao assunto:

1. O que é Logaritmo e para quê serve? Introdução para iniciantes!
2. Como resolver um Logaritmo?
3. Definição, condição de existência e consequências!
4. Exemplo de resolução do Log.
5. Quais são as propriedades do Logaritmo? (log de quociente, produto, soma, subtração, potência e muito mais!)
6. Casos especiais: log neperiano, mudança de base, etc.

Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!

O que é Logaritmo e para quê ele serve? 

O Logaritmo é uma ferramenta matemática muito importante para a humanidade!

No século XVII (1600), essa ferramenta  foi desenvolvida para auxiliar na resolução de cálculos, principalmente os que envolvem potências.

John Napier foi o matemático que desenvolveu esse auxílio muito utilizado na física, biologia, química, computação e até na geografia! Normalmente é usado no cálculo de terremotos, mas também pode ajudar no cálculo de populações.

Indo direto ao ponto:

O logaritmo é a uma operação que utilizamos para descobrir o expoente de uma base que já foi dada. A descoberta de um expoente para essa base deve fazer com que eles se igualem à uma potência modelo.

Esse nome veio do grego: “Logos – razão” e “arithmos – números”. Mas vamos apelidar como Log para facilitar as coisas e ficarmos mais à vontade! 

Como resolver um logaritmo?

Para resolver o log com melhor precisão, outros matemáticos oficializaram definições e suas consequências matemáticas. Para entendê-las, precisamos conhecer os elementos que constituem o símbolo do log e como lê-los. 

Além disso, é necessário conhecer as propriedades da potenciação. Isso porque o gráfico do Log nos mostra que ele é o inverso das funções exponenciais, demonstrando que ambas coisas estão estritamente relacionadas.

Por isso, para resolver um log, bastará aplicar a definição literalmente, traduzindo-a em números. E lembrar de recorrer às propriedades quando for o caso adequado!

Vamos conhecer quais são esses elementos, definições, exemplos e propriedades:

Definição do Logaritmo e Condições de Existência

A forma genérica de um log qualquer, é composta por três elementos:

• a → base
• b → logaritmando
• x → logaritmo

Os quais são organizados na escrita matemática da seguinte forma:

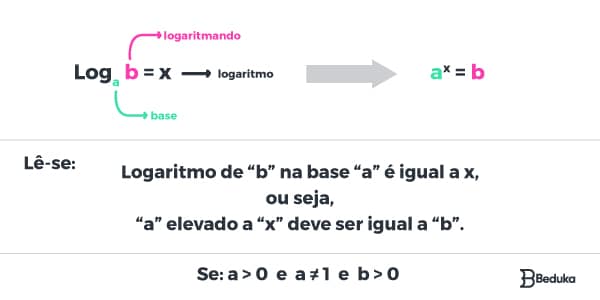
Matematicamente falando, a definição formal de log é:

Ao considerar dois números “a” e “b” reais positivos, com a ≠ 1, o logaritmo de “b” na base “a” é o número “x” somente se “a” elevado a “x” for igual ao número “b”.

É preciso que o logaritmando “b” seja positivo, pois se ele for negativo significa que o “a” também era e isso não existe.

É preciso que a base “a” seja diferente de 0. Caso fosse 0, seria impossível resolver aplicando a definição. Isso porque na potenciação não existe base 0.

Também é preciso que a base “a” seja positiva. Se fosse negativa, daria possibilidade de o “b” também ser, o que não pode.

Por fim, a base “a” deve ser diferente de 1. Se fosse 1, teríamos sempre o mesmo valor para o log e não seria possível solucionar as diversas questões.

Consequências da definição

Como temos um definição e condições de existências, podemos tirar algumas conclusões óbvias e diretas disso. Veja:

ATENÇÃO!

Nem sempre é possível escrever o log como foi representado nas imagens: com a base menorzinha e em baixo, pois nem todos os sites posicionam estes símbolos.

Por isso, atente-e se que log₂ 7 deve ser lido como “log de 7 na base 2”.

• Sempre que o logaritmando for 1 o resultado será 0, independentemente da base. As regras da potenciação também dizem que todo número elevado a zero resulta em 1, então x = 0. Veja:

log₇ 1 = x, pois 7^x = 1

• Sempre que o logaritmando for igual à base, o resultado será 1. Isso também ocorre por causa das regras da potenciação: todo número elevado a 1 resulta nele mesmo:

se log₉ 9 = x, então 9¹ = 9, logo,  9^x = 9¹ e x = 1.

• Sempre que houver logaritmando igual à base e esta base possuir um expoente, o resultado será o próprio expoente:

log₈ 8² = x, pois 8^x = 8², então x = 2.

• Sempre que houver 2 logaritmos com bases iguais em uma igualdade, os logaritmandos também serão iguais:

log₃^b = log₃^c, então b = c.

Exemplo de resolução do Log

Vamos aplicar a definição para resolver os logs com valores numéricos reais:

Descubra o valor de log₃ 81.

Resolução

Fazemos a seguinte leitura: “log de 81 na base 3 é igual a quanto?”, ou seja, preciso descobrir a qual número devo elevar a base 3 para que resulte em 81”. Usando a definição, temos:

log₃ 81 = x    →    3^x = 81

Para encontrar esse valor, devemos fatorar o número 81, pois assim saberemos se ele pode ser composto apenas multiplicando o 3 certo número de vezes:

Como as bases são iguais e ambas as potências estão numa equação de igualdade, então os expoentes também são iguais. Assim:

x = 4

Quais são as propriedades do Logaritmo?

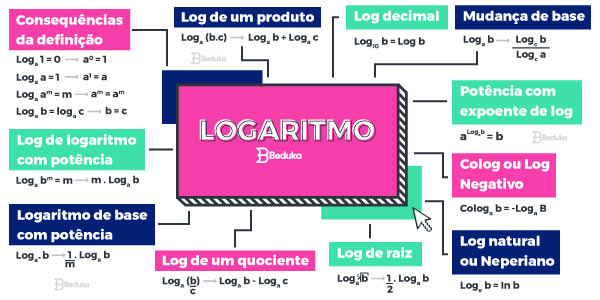
As propriedades nos auxiliam a resolver os logs em certas situações. Elas podem não fazer muito sentido vistas assim, soltas. 

Porém, alguns exercícios funcionam assim:

São dados, por exemplo, os valores numéricos de log₁₀ 2 e log₁₀ 3, pedindo que você ache o log₁₀ 6. São nessa situações que utilizamos as propriedades!

Todos os exemplos citados satisfazem a condição de existência. Agora veja como aplicar essas propriedades:

Logaritmo de um produto → soma de logaritmos

Quando houver um produto de fatores no logaritmando, o logaritmo corresponde à soma dos logaritmos individuais de cada fator, mantendo-se a mesma base para ambos. 

Exemplo

Log₃ (30) → log₃ (3 x 10) → log₃ 3 + log₃ 10

Logaritmo de um quociente → subtração de logaritmos

Quando houver uma divisão de fatores no logaritmando, o logaritmo corresponde à subtração dos logaritmos individuais de cada fator, mantendo-se a mesma base.

Exemplo

Log₃ 2 → log₃ (6 / 3) → log₃ 6 – log₃ 3

Log de logaritmando com potência

Quando o logaritmando for uma potência, o expoente dela passa a multiplicar todo o logaritmo restante.

Exemplo

Log₇ b³ →  3 log₇ b

Logaritmo de base com potência

Quando a base for uma potência, o expoente dela é invertido e passa a multiplicar todo o logaritmo restante.

Exemplo

Log_3² 8 →  ½ log₃ 8

Logaritmo de Raiz

Vimos no artigo potenciação que um número elevado à uma fração pode ser transformado em raiz: 4 elevado a ½ é o mesmo que fazer a raiz quadrada de 4 e 8 elevado a ⅓ é o mesmo que fazer a raiz cúbica de 8.

Assim, quando houver uma raiz no logaritmando faremos o seu inverso, ou seja, a potência correspondente. Depois, prosseguimos com a propriedade do logaritmo de potência: o expoente passa a multiplicar todo o logaritmo.

Exemplo 

Log₂ √4 → ½ log₂ 4

Casos especiais de Logaritmos

Além das propriedades, você pode se deparar com algumas formas de logaritmo que “assustam”. Vamos entendê-las, pois só teme quem não conhece!

Logaritmo decimal

Quando um logaritmo possui a base igual a 10, será chamado logaritmo decimal. Contudo, definiu-se que quando ele for decimal, não é necessário escrever a base 10.

Portanto, se você se deparar com algo do tipo “log 4”, não ache que está faltando algo! O 10 na base está implícito!

Logaritmo Natural ou Neperiano

John Napier não só desenvolveu o cálculo do logaritmo, como também uma notação específica para quando usarmos a constante de Euler.

Você já deve ter usado o pi “π” na geometria, e sabemos que seu valor aproximado é 3,14. Existe também a constante de Euler, cujo símbolo é o “e” vale aproximadamente 2,7.

Quando a base do logaritmo for o “e”, definiu-se que não se escreveria log_e b = x. Mas sim a seguinte notação:

in b = x

O “in” deixa implícito que se trata de um log de base “e”.

Potência com log no expoente

Quando uma potência estiver elevada a um expoente que for logaritmo, se a base da potência for a mesma da base do logaritmo, o resultado será o logaritmando.

Exemplo

7 ^{log₇ 4} → o resultado será 4.

Logaritmo Negativo ou Colog

O cologaritmo nada mais é que o log negativo. Mantém-se a condição de que base e logaritmando não podem ser negativos, o logaritmo é que pode. 

Assim, quando nos depararmos com colog₂ 4, basta fazer – log₂ 4.

Isto equivale a dizer que há um “-1” multiplicando o log.

Mudança de base de Logaritmo

Por último, eis um recurso muito utilizado. Você já pensou o que fazer quando as bases estão diferentes e nenhuma propriedade se aplica?

Nesta situação, basta fazer a mudança da base antiga para aquela que nos convêm!

Exemplo

Supondo que temos o seguinte cálculo para ser resolvido: Log₃ 2. Mas foi dado apenas o valor numérico de log 2 e log 3.

Isso significa que é conveniente transformar o log inicial para um que tenha a base 10. Assim, poderemos substituir os valores que já foram dados!

Para isso, basta armar uma divisão entre dois logs de mesma base (o valor que queremos colocar nela).

• No logaritmando do numerador, mantemos o logaritmando do log inicial.
• No logaritmando do denominador, colocamos a antiga base do log original.

Assim, se quisermos fazer uma mudança de base do log₃ 2 para a base 10, será da seguinte forma:

log 2 / log 3

Como podemos colocar a base que quisermos, poderíamos escrever também: log₂ 2 / log₂ 3 ou log₃ 2 / log₃ 3. Só que estas mudanças não seriam aproveitáveis, pois os valores foram dados para logs decimais nesta questão.

Gostou do nosso artigo sobre Logaritmo? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC e muito mais.

Experimente agora!