A Função Afim, também chamada de Função de 1° Grau, é um polinômio descrito pela regra geral y = ax + b. O maior expoente da variável “x” é 1 e o seu gráfico é uma reta inclinada. Ela ainda possui um coeficiente angular “a” e um linear “b”, sendo muito utilizada para resolver problemas matemáticos!
Neste artigo sobre Função Afim você encontrará:
- Função Afim: o que é uma função, definição, forma geral e componentes
- Gráfico da Função Afim e como resolvê-la
- Coeficiente angular e linear
- Tipos de função afim: crescente, decrescente, identidade e constante
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que é uma Função?
Antes de aprender o que é uma Função Afim, precisamos entender o conceito de função! Quando dizemos que “fulano vive em função do seu trabalho”, a primeira ideia que vem à cabeça é de uma relação de dependência. Isso também se aplica à matemática!
Portanto, a função é uma operação matemática que relaciona dois conjuntos que se dependem. Naquele que chamamos de Domínio, há todas as possibilidades de valores para o “x”. No Contradomínio, há as possibilidade de valores para “y”.
Cada elemento do Domínio só pode se ligar a um do Contradomínio, pois evidencia que só há um resultado para solucionar aquela questão. Essa relação entre os elementos se dá pela lei de formação, que é a lei que define uma função.
Portanto, para cada valor que x tiver na função, pode-se estabelecer um valor de y. Por isso dizemos que “y está em função de x”. Dessa forma, x e y são conhecidos, respectivamente, como variável independente e variável dependente.
O que é Função Afim, Fórmula Geral e Definição
A Função Afim é o tipo mais básico de função, aprendemos ela primeiro para depois continuarmos com as outras (2° grau, exponencial, etc.).
Ela é um polinômio de primeiro grau, isto é, uma expressão matemática com vários algarismos, operações, “letras” para se descobrir seu valor numérico e cujo maior expoente é 1.
A função afim, também pode ser chamada de função do 1º grau, e é definida como f : ℝ→ℝ, o que significa que seus números devem pertencer ao conjunto dos número Reais.
Sua regra geral é:
- f(x) = ax + b
Sendo que:
- “a” é chamado de coeficiente angular
- “b” é chamado de coeficiente linear
- “x” é a variável independente
- f(x) = y , ou seja, a variável dependente
- “a” e “b” pertencem aos números reais
Alguns exemplos numéricos desse tipo de função são:
- f(x) = x + 15
- h(x) = ⅓ x
- g(x) = x – 2
- Y = 2x + 4
O que é Coeficiente Angular e Linear
- Coeficiente angular (a):
É o “a” da função, o que fica junto do x. No gráfico, é a tangente do ângulo α (alfa) formado pela intersecção entre a reta da função e o eixo x. (veremos no próximo tópico a imagem do gráfico). Este coeficiente é responsável por determinar a inclinação da reta no gráfico.
- Coeficiente linear (b):
É o “b” da função, o que fica longe do x. No gráfico, é o ponto em que a reta da função corta o eixo Y, ou seja, a interseção desses elementos.
Como resolver uma Função Afim
Para resolver uma Função Afim, basta saber a sua lei de formação, substituir os valores dados e encontrar os que faltam da mesma forma com que se resolve uma Equação de 1° Grau.
Exemplo
- Carlos é lojista e ganha um salário mensal de R$ 3.000,00. Além disso, a cada produto em destaque vendido, ele ganha uma comissão de 3% do valor deste produto. Se ele vendeu 120 peças em destaque, qual será o seu salário neste mês?
Solução
A primeira coisa que precisamos fazer é definir a regra de formação. Vamos chamar o valor final do salário de “f(x)” e recordar que 3% de cada produto vendido equivale a 0,03x. Então, podemos escrever que sua lei de formação é:
f(x) = 0,03x + 2000
Agora, basta substituir “120” no “x”, pois foi essa a quantidade de produtos em destaque vendido neste mês. Teremos:
f(x) = 0,03.120 + 2000
f(x) = 3,6 + 2000
f(x) = 2003,6
Portanto, neste mês o lojista ganhou um total de R$ 2003,60.
Qual é o Gráfico da Função Afim e como achar suas raízes?
O que chamamos de “raiz da função” é o ponto em que ela atravessa o eixo x, isto é, o ponto em que y = 0. Ache o valor do x para y=0 e você terá encontrado a raiz.
Portanto, para descobrir a raiz de uma função afim, basta substituir o y por 0. Ao fazer isso, teremos:
f(x) = ax + b
0 = ax + b
ax = -b
x = -b/a
- Logo, a raiz da Função Afim é o ponto -b/a no eixo x. É importante destacar que as funções de 1º grau têm apenas 1 raiz.
- O gráfico da função afim é uma reta, então só precisamos de dois pontos para traçá-lo.
Eles podem ser os pontos que você quiser (pegue a regra geral da função e vá jogando valores no “x” para ver qual o par “y” que satisfaz), mas na falta de tempo e/ou espaço, é mais fácil definir como primeiro ponto a raiz, que você já viu com se calcula. O segundo pode ser o ponto em que a reta atravessa o eixo y, isto é, o b que está indicado na fórmula.
Vamos fazer dos dois modos, veja:
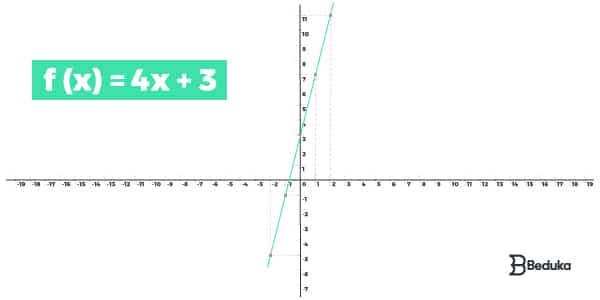
1.Construa o gráfico da função f(x) = 4x +3
A raíz será o ponto em que a função toca o eixo x, ou seja, o seu y deve ser 0. Portanto:
0 = 4x +3
-4x = 3
x = 3 / -4
x = – 0,75
Portanto, o primeiro ponto da reta no gráfico é definido pelo par ordenado (x e y) = (- 0,75 e 0)
Já sabemos pela fórmula que quando a reta toca o eixo y no valor indicado por “b”, portanto temos o segundo par ordenado da reta (0 e 3).
2.Construa o gráfico da função f (x) = 4x + 3.
Para construir o gráfico desta função, vamos atribuir valores arbitrários aleatórios para x, e calcular o valor correspondente para y. Supondo os valores -2, -1, 0, 1 e 2 para x, temos a formação do seguintes pares de pontos na reta:
f (- 2) = 4. (- 2) + 3 = – 8 + 3 = – 5, então (-2 e -5)
f (- 1) = 4 . (- 1) + 3 = – 4 + 3 = -1, então (-1 e -1)
f (0) = 4 . 0 + 3 = 3, então (0 e 3)
f (1) = 4 . 1 + 3 = 7, então (1 e 7)
f (2) = 4 . 2 + 3 = 11, então (2 e 11)
O gráfico de f (x) = 4x + 3 será:
Tipos de função Afim
Existem alguns tipos específicos de função afim que recebem nomes diferentes. Vamos ver quais são as características de cada uma:
Função Afim Crescente e Decrescente
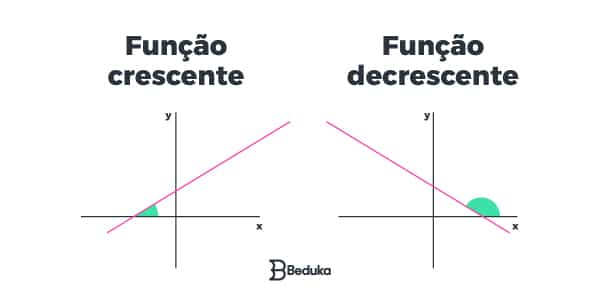
- Uma Função Afim é crescente quando o seu coeficiente angular é positivo (a > 0), ou seja, ao atribuir valores cada vez maiores para “x”, o “y” também aumenta.
- Uma Função Afim é decrescente quando o seu coeficiente angular é negativo (a < 0), ou seja, ao atribuir valores cada vez maiores para “x”, o “y” diminui.
Função Linear
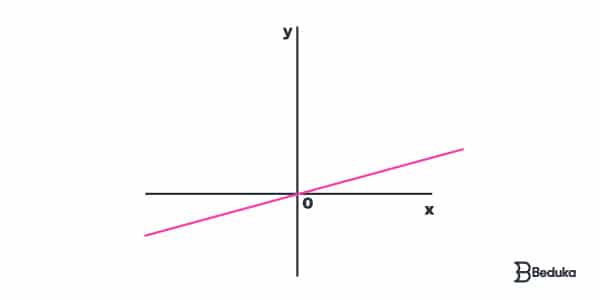
A Função Afim é chamada de Linear quando b = 0, sendo que a ≠ 0. Nesses casos, o gráfico necessariamente passa pelo ponto de origem (0,0).
Função Identidade
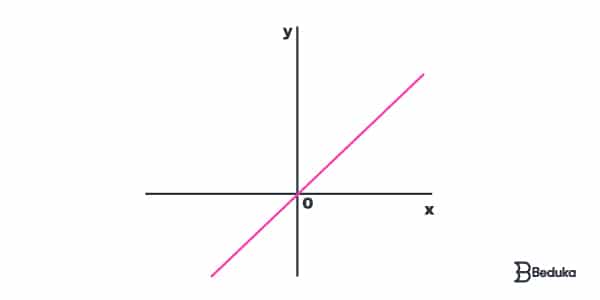
A Função Afim é Identidade quando a = 1 e b = 0. Nesses casos, o gráfico necessariamente passa pelo ponto (0,0), e o ângulo α é de 45º.
Além disso, essa reta é bissetriz do 1º e 3º quadrantes, ou seja, divide os quadrantes em dois ângulos iguais, conforme indicado na imagem abaixo:
Função Constante
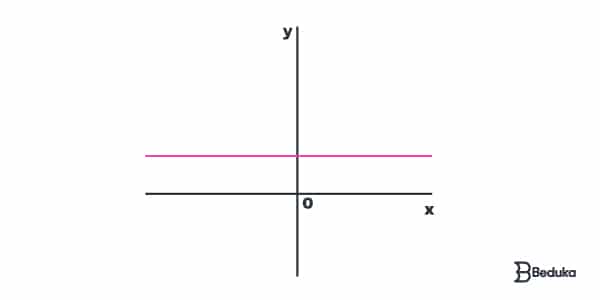
A Função Afim é constante quando a = 0. Nesses casos, o gráfico é paralelo ao eixo x.
Gostou do nosso artigo sobre Função Afim? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





