O logaritmo facilita o cálculo de operações. Leia o resumo e pratique com os exercícios de logaritmo.
O logaritmo é uma das matérias que caem recorrentemente nas principais provas e vestibulares. Como sabemos que estudar matemática é um desafio para muitos estudantes resolvemos esclarecer algumas questões nesse resumo. Na prova do ENEM, no caderno de Matemática e suas Tecnologias, pode ser cobrado alguns exercícios de logaritmo, então treine para conseguir uma boa nota.
O que é Logaritmo?
O logaritmo é usado principalmente na área da matemática, porém essa ferramenta também pode ser utilizada em outros campos da ciência, como por exemplo, na geografia, química e até mesmo na computação, como programador.
O principal objetivo do logaritmo é facilitar o cálculo de contas. O estudioso Jonh Napier é considerado um dos pioneiros desse estudo sobre logaritmos. Ele conseguiu transformar produtos em soma, divisões em subtrações e potências em multiplicações, sendo um avanço para o processo de operações, pois deixava os cálculos mais fáceis de serem resolvidos.
Porém, não para por aí! Após os estudos de Jonh Napier, outros matemáticos conseguiram formalizar definições e propriedades e desenvolver ainda mais o processo das operações com a criação da tábua de logarítmos.
Qual a definição de logaritmo?
Veja o esboço gráfico abaixo:
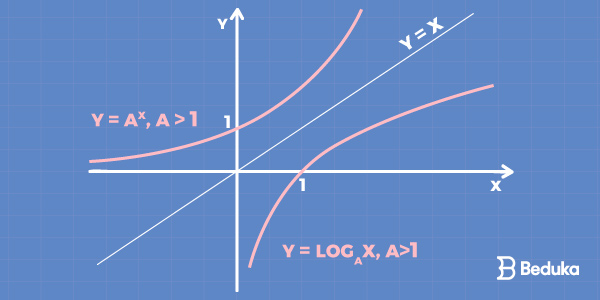
Do lado direito é possível ver o gráfico da função logaritmo e à esquerda temos a inversa exponencial.
Abaixo está a definição matemática, mas já vou te dizer em termos bem simples: o logaritmo tem os elementos da potenciação organizados de forma diferente. Sem saber potenciação não vai ter jeito de entender essa matéria.
Vamos pensar em dois números reais positivos representados pelas letras a e b, sendo a ≠ 0. Já o logaritmo de b na base a é o número x se, e somente se, a for elevado a x seja igual ao número representado pela letra b. Exemplificando:

Então:
a: base
b: logaritmando
x: logaritmo
Alguns exemplos são:

Cálculo do logaritmo
O cálculo do logaritmo necessita que exista um número que, quando for elevado a base, dê como resultado o logaritmando.
Como por exemplo o Log 1000, para podermos calcular esse logaritmo é preciso encontrar um número que ao ser elevado a 10, tenha como resultado 1000, para encontrarmos esse número é preciso elaborar uma equação exponencial, veja:
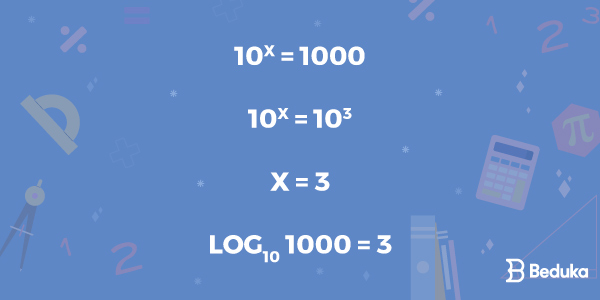
Então o Log 1000 é igual a 3.
Depois desse resumo é hora de colocar em prática com as questões abaixo! Teste seus conhecimentos com os exercícios de logaritmo e confira as respostas no gabarito!
Exercícios de Logaritmo
Baixe o melhor plano de estudos gratuito que você encontrará na internet.
1 – (MACK-SP) – O volume de um líquido volátil diminui 20% por hora. Após um tempo t, seu volume se reduz à metade. O valor que mais se aproxima t é:
(Use log 2 = 0,30)
a) 2h 30min
b) 2h
c) 3h
d) 3h 24min
e) 4h
2 – (FUVEST 2010) – A magnitude de um terremoto na escala Richter é proporcional ao logaritmo, na base 10, da energia liberada pelo abalo sísmico. Analogamente, o pH de uma solução aquosa é dado pelo logaritmo, na base 10, do inverso da concentração de íons H+. Considere as seguintes afirmações:
I. O uso do logaritmo nas escalas mencionadas justificase pelas variações exponenciais das grandezas envolvidas.
II. A concentração de íons H+ de uma solução ácida com pH 4 é 10 mil vezes maior que a de uma solução alcalina com pH 8.
III. Um abalo sísmico de magnitude 6 na escala Richter libera duas vezes mais energia que outro, de magnitude 3.Está correto o que se afirma somente em:
a) I.
b) II.
c) III.
d) I e II.
e) I e III.
3 – (UDESC 2008) – Sabendo que log3(7x – 1) = 3 e que log2(y³ + 3) = 7 pode-se afirmar que logy(x² + 9) é igual a:
a) 6
b) 2
c) 4
d) -2
e) -4
4 – (UFMG 2009) – Numa calculadora científica, ao se digitar um número positivo qualquer e, em seguida, se apertar a tecla log, aparece, no visor, o logaritmo decimal do número inicialmente digitado.Digita-se o número 10.000 nessa calculadora e, logo após, aperta-se, N vezes, a tecla log, até aparecer um número negativo no visor. Então, é CORRETO afirmar que o número N é igual a:
a) 2
b) 3
c) 4
d) 5
5 – (UDESC 2008) – Se log a b =3 e log ab c : 4 , então log a c e :
a) 12
b) 16
c) 24
d) 8
e) 6
6 – (UFRGS 2017) – Se log5 x = 2 e log10 y = 4, então log20 y/x é:
a) 2
b) 4
c) 6
d) 8
e) 10
7 – (UFRGS 2016) – Se 10x = 20y , atribuindo 0,3 para log 2 , então o valor de x/y é:
a) 0,3.
b) 0,5.
c) 0,7.
d) 1.
e) 1,3.
Achou dificíl? Calma, sem desespero! Confira as respostas dos exercícios de logaritmo no gabarito abaixo.
Respostas dos Exercícios de Logaritmo
Exercício resolvido da questão 1 –
c) 3h
Exercício resolvido da questão 2 –
d) I e II.
Exercício resolvido da questão 3 –
b) 2
Exercício resolvido da questão 4 –
b) 3
Exercício resolvido da questão 5 –
b) 3
Exercício resolvido da questão 6 –
a) 2
Exercício resolvido da questão 7 –
e) 1,3.
Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos Exercícios de Logaritmo? Compartilhe com os seus amigos e comente abaixo sobre áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





