A Fórmula de Bháskara é um método usado para resolver equações do segundo grau. Com ela, encontra-se as raízes reais por meio dos coeficientes (ax² + bx + c = 0). Seu nome é uma homenagem ao indiano que a inventou, o matemático Bhaskara Akaria (1114 – 1185). Veja nossa lista de exercícios sobre a fórmula de Bhaskara.
Quando você terminar as questões sobre Fórmula de Bhaskara, faça nosso Simulado Enem. Coloque em prática todo o seu estudo, escolhendo as matérias que deseja treinar.
Criada para resolver problemas envolvendo equações do 2° grau, a Fórmula de Bháskara é um dos conteúdos mais importantes para o ENEM e outros vestibulares.
Neste post, escrevemos para você um resumo com tudo o que você precisa saber e ao final, listamos exercícios sobre a Fórmula de Bháskara.
A Fórmula de Bháskara
A Fórmula de Bhaskara é descrita com a seguinte expressão:
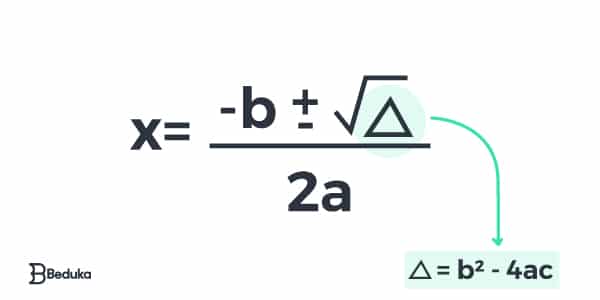
O objetivo da Fórmula de Bhaskara é encontrar as raízes da equação de segundo grau.
Uma equação de segundo grau é descrita, genericamente, como:
ax² + bx + c = 0
Raízes são os valores numéricos que o X pode assumir, a partir do sinal que usamos antes da raiz de delta. Sendo as possibilidades, sinal negativo ou positivo.
Como resolver uma equação do 2º grau? Veja o passo a passo de como usar a fórmula de Bhaskara
Daqui para frente, iremos explicar passo a passo como resolver uma equação de segundo grau para que você chegue preparado nos exercícios.
1° Passo: identifique os coeficientes da equação
Na equação, identifique quais números estão no lugar das letras a, b e c. Cada letra dessas é um coeficiente.
Dica do Beduka: Normalmente, uma equação não virá com a, b e c, mas com números que ocuparão essa posição. Na hora da prova, você é que deverá saber identificar os números que representam essas letras, para substituí-los nas equações. Seja descobrindo o valor de delta, seja descobrindo as raízes da equação.
2° Passo: calcular a discriminante, ou seja, o delta
Discriminante é a equação representada pela letra delta (sim, aquela que parece um triângulo exibida lá no início do post). Resolva essa equação e descubra o valor de delta, assim, você poderá pegar esse valor e inseri-lo na Fórmula de Bhaskara.
Apenas os valores de delta já te dão uns spoilers sobre o resultado da equação:
- Delta menor do que zero: equação não possui raízes reais;
- Delta igual a zero: a equação possui duas raízes iguais;
- Delta maior do que zero: a equação possui duas raízes distintas reais.
3° Passo: substitua o valor de delta e dos coeficientes (a e b)
No lugar das letras e do símbolo de delta, coloque os valores numéricos, os números mesmo! Simplesmente você fará uma substituição.

4° Passo: descubra as raízes da equação
Observando a Fórmula de Bhaskara, você perceberá que antes da raiz de delta, existem dois sinais. Um sinal de adição (+) e outro de subtração (-). Bem, você terá que realizar dois cálculos. Um usando a fórmula com o sinal positivo e o outro com o negativo. Ficando assim:
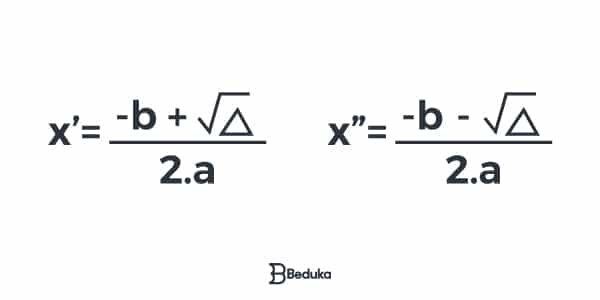
X’ e X” são as raízes da equação.
Dica do Beduka: lembre-se de olhar os casos onde você já tem os “spoilers”, ou seja, já tem informações do resultado a partir do valor do delta. Isso pode lhe garantir um bom tempo de vantagem na hora da prova.
Viu como é possível aprender de forma bastante simples com o Beduka? Que tal agora praticar para ter certeza que aprendeu, assim você pode atestar que está totalmente preparado.
Exercícios sobre a Fórmula de Bhaskara
Chegou o momento de colocar na prática todo o seu conhecimento fazendo exercícios sobre a Fórmula de Bhaskara.
Parabéns por ter lido até aqui!!!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
1- (ENEM 2013) A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do instante do desligamento (t = 0) e varia de acordo com a expressão (t em minutos):

Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge temperatura de 39 °C. Qual o tempo mínimo de espera, em minutos, após desligar o forno, para que a porta possa ser aberta?
a) 19,0
b) 19,8
c) 20,0
d) 38,0
e) 39,0
2- (UFMT – COPEL) Dada a equação do segundo grau x² – 3x – 4 = 0, assinale a alternativa que apresenta, respectivamente, os valores de Δ e da soma das raízes dessa equação.
a) 25 e 3
b) 25 e 5
c) 36 e 2
d) 36 e 4
3- (IFSC/2017) Pedro é pecuarista e, com o aumento da criação, ele terá que fazer um novo cercado para acomodar seus animais. Sabendo-se que ele terá que utilizar 5 voltas de arame farpado e que o cercado tem forma retangular cujas dimensões são as raízes da equação x² – 45x + 500 = 0, qual a quantidade mínima de arame que Pedro terá que comprar para fazer esse cercado?
Assinale a alternativa CORRETA.
a) 545m
b) 500m
c) 225m
d) 450m
e) 200m
4- (IFBA/2017) Durante as competições Olímpicas, um jogador de basquete lançou a bola para o alto em direção à cesta. A trajetória descrita pela bola pode ser representada por uma curva chamada parábola, que pode ser representada pela expressão:
h = –2×2 + 8x
(onde “h” é a altura da bola e “x” é a distância percorrida pela bola, ambas em metros)
A partir dessas informações, encontre o valor da altura máxima alcançada pela bola:
a) 4m
b) 6m
c) 12m
d) 10m
e) 8m
5- (IFSC/2017) Dada a equação quadrática 3×2 + 9x – 120 = 0, determine suas raízes.
Assinale a alternativa que contém a resposta CORRETA:
a) -9 e 15
b) -10 e 16
c) -8 e 5
d) -5 e 8
e) -16 e 10
Respostas dos exercícios sobre a Fórmula de Bhaskara
Exercício resolvido da questão 1 –
Alternativa correta: d) 38,0
Exercício resolvido da questão 2 –
Alternativa correta: a) 25 e 3
Exercício resolvido da questão 3 –
Alternativa correta: d) 450m
Exercício resolvido da questão 4 –
Alternativa correta: e) 8m
Exercício resolvido da questão 5 –
Alternativa correta: c) -8 e 5
Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos Exercícios sobre a Fórmula de Bhaskara? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.





