Exercícios de Semelhança de Triângulos com Gabarito

A Semelhança de Triângulo é o estudo da proporção entre dois ou mais triângulos. Triângulos com ângulos e lados proporcionais são classificados como proporcionais integralmente. Leia nosso resumo e coloque seu conhecimento em prática com exercícios selecionados dos maiores vestibulares do Brasil.

Quando você terminar os Exercícios de Semelhança de Triângulos, faça nosso Simulado Enem. Coloque em prática todo o seu estudo, escolhendo as matérias que deseja treinar.

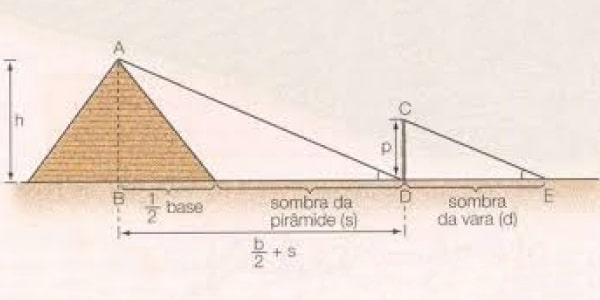
A Semelhança de Triângulo é um conhecimento tão poderoso que permitiu que Tales de Mileto, há mais de 2.500 anos atrás, conseguisse medir o tamanho da pirâmide do Egito com uma vara.

Esse gênio da Matemática fincou a vara no chão próximo à pirâmide e percebeu que a sombra que a vara fazia era proporcional à sombra que a pirâmide fazia.

Sendo que ambas as sombras formavam um triângulo.

Daí foi só usar a Semelhança de Triângulos para calcular a altura da pirâmide.

Incrível, não?

Agora vamos te ensinar passo a passo da teoria que permitiu esse feito protagonizado por Tales de Mileto.

• Entenda Semelhança de Triângulos, seus casos, regras e veja exemplos

O que é Semelhança de Triângulos?

A Semelhança de Triângulo é o estudo da proporção entre dois ou mais triângulos. Triângulos com ângulos e lados proporcionais são classificados como proporcionais integralmente.

Quando comparamos duas figuras é fácil tirar conclusões: algumas vezes são iguais (congruentes), outras são parecidas (semelhantes) ou ainda completamente distintas (diferentes). 

Quando elas são iguais é como se fossem réplicas

Quando elas são distintas, não há nada em comum. 

Agora, quando são semelhantes, significa dizer que existe proporcionalidade entre lados e ângulos, ou seja, é como se você pegasse uma figura e a ampliasse, assim, todos os elementos aumentaram na mesma proporção.

Quando Posso dizer que Dois Triângulos são Semelhantes?

Dois triângulos só serão semelhantes se todas as divisões de lados correspondentes resultarem na mesma constante e tiverem ângulos congruentes

Lembra do Tales de Mileto? 

Observe como ele percebeu dois triângulos semelhantes a partir da sombra da pirâmide e da vara.

Altura da vara é proporcional à altura da pirâmide, assim como os ângulos e os lados. 

Veja a seguir:

• Teste o seu conhecimento sobre o Teorema de Tales de Mileto.

Quais são os 3 casos de Semelhança de Triângulos?

1- Caso Ângulo Ângulo (AA)

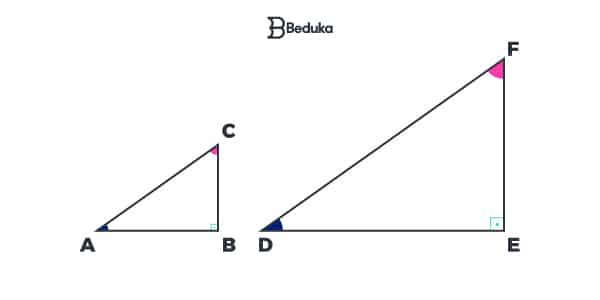
Os dois triângulos são considerados semelhantes por possuírem dois ângulos correspondentes congruentes.

Atenção:

Não saia por aí acreditando que todos os pares de triângulos com 2 ângulos iguais são semelhantes.

É necessário que também sejam ângulos correspondentes.

2- Caso Lado Lado Lado (LLL)

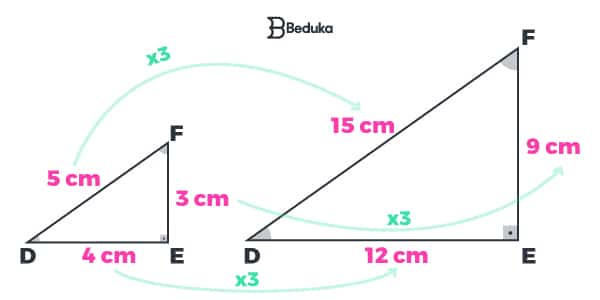
Neste caso, os três lados dos triângulos são proporcionais. 

Na imagem acima, verificamos que todos os tamanhos dos lados do triângulo menor, quando multiplicados por 3, resultam no tamanho do lado correspondente do triângulo maior.

3- Caso Lado Ângulo Lado (LAL)

Dois triângulos que possuem dois lados correspondentes proporcionais e o ângulo entre eles congruente são semelhantes. 

Vamos tentar descobrir o valor de X neste triângulo semelhante:

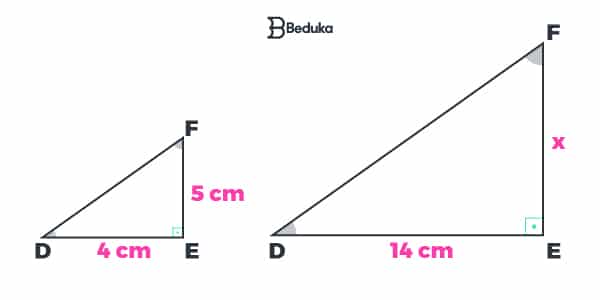
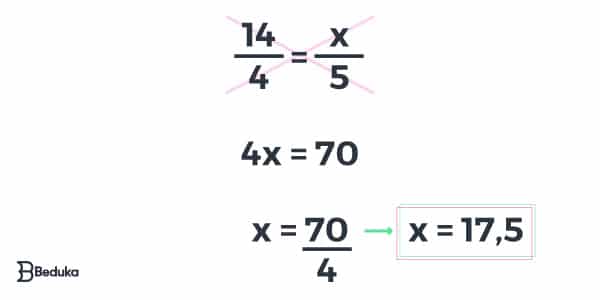
Agora faça você como Tales de Mileto e coloque seu conhecimento em prática com nossos Exercícios de Semelhança de Triângulos

Exercícios de Semelhança de Triângulos 

No início até assusta, mas agora sei que com esse resumo tudo ficou mais claro para você. Que tal testar seu conhecimento com Exercícios de Semelhança de Triângulos. 

Parabéns por ter lido até aqui!!! 

Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.

Questão 1 – (Unesp) A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:

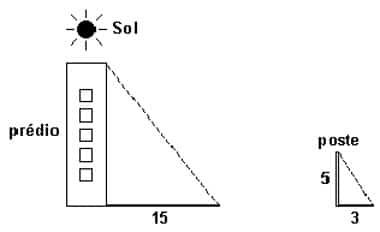
a) 25

b) 29

c) 30

d) 45

e) 75

Questão 2 – (Unirio) Numa cidade do interior, à noite, surgiu um objeto voador não identificado, em forma de disco, que estacionou a 50 m do solo, aproximadamente. Um helicóptero do exército, situado a aproximadamente 30 m acima do objeto, iluminou-o com um holofote, conforme mostra a figura anterior. Sendo assim, pode-se afirmar que o raio do disco mede, em m, aproximadamente:

a) 3,0

b) 3,5

c) 4,0

d) 4,5

e) 5,0

Questão 3 – (Fuvest  2017) Na figura, o retângulo ABCD tem lados de comprimento AB = 4 e BC = 2. Sejam M o ponto médio do lado B C em moldura superior fecha moldura e No ponto médio do lado C D em moldura superior fecha moldura. Os segmentos A M em moldura superior fecha moldura espaço e espaço A C em moldura superior fecha moldura interceptam o segmento B N em moldura superior fecha moldura nos pontos E e F, respectivamente.

Questão Fuvest 2017 semelhança de triângulos

A área do triângulo AEF é igual a

a) 24/25

b) 29/30

c) 61/60

d) 16/15

e) 23/20

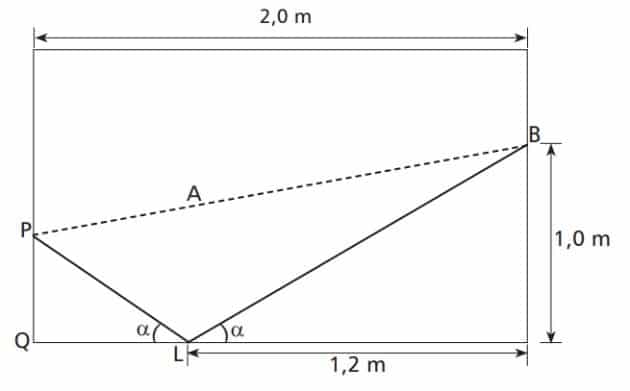
Questão 4 – (Cefet 2015) A ilustração a seguir representa uma mesa de sinuca retangular, de largura e comprimento iguais a 1,5 e 2,0 m, respectivamente. Um jogador deve lançar a bola branca do ponto B e acertar a preta no ponto P, sem acertar em nenhuma outra, antes. Como a amarela está no ponto A, esse jogador lançará a bola branca até o ponto L, de modo que a mesma possa rebater e colidir com a preta.

Se o ângulo da trajetória de incidência da bola na lateral da mesa e o ângulo de rebatimento são iguais, como mostra a figura, então a distância de P a Q, em cm, é aproximadamente

a) 67

b) 70

c) 74

d) 81

Questão 5 – (Colégio Militar/RJ  2015) Em um triângulo ABC, os pontos D e E pertencem, respectivamente, aos lados AB e AC e são tais que DE / / BC . Se F é um ponto de AB tal que EF / / CD e as medidas de AF e FD e são, respectivamente, 4 e 6, a medida do segmento DB é:

a) 15.

b) 10.

c) 20.

d) 16.

e) 36.

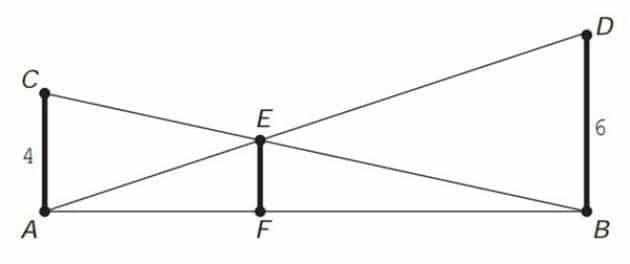
Questão 6 – (Enem  2013) O dono de um sítio pretende colocar uma haste de sustentação para melhor firmar dois postes de comprimentos iguais a 6 m e 4 m. A figura representa a situação real na qual os postes são descritos pelos segmentos AC e BD e a haste é representada pelo segmento EF, todos perpendiculares ao solo, que é indicado pelo segmento de reta AB. Os segmentos AD e BC representam cabos de aço que serão instalados.

Qual deve ser o valor do comprimento da haste EF?

a) 1 m

b) 2 m

c) 2,4 m

d) 3 m

e) 26 m

Gabarito dos Exercícios de Semelhança de Triângulos

Exercício resolvido da questão 1 –

Alternativa correta: a) 25

Exercício resolvido da questão 2 –

Alternativa correta: a) 3,0

Exercício resolvido da questão 3 –

Alternativa correta: d) 1615

Exercício resolvido da questão 4 –

Alternativa correta: a) 67

Exercício resolvido da questão 5 –

Alternativa correta: a) 15.

Exercício resolvido da questão 6 –

Alternativa correta: c) 2,4 m

Estude para o Enem com o Simulado Beduka. É gratuito!

Gostou dos nossos Exercícios de Semelhança de Triângulos? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.