O Teorema de Tales foi desenvolvido pelo filósofo chamado Tales de Mileto, nascido na Grécia em 624 antes de Cristo. O seu teorema foi um avanço importante para a matemática, principalmente na geometria. Faça os exercícios sobre Teorema de Tales e leia o resumo da matéria.
Se você tem dificuldades em matemática, confira esses exercícios sobre Teorema de Tales, pois, desta forma, você estará mais bem preparado para o ENEM e outros principais vestibulares.
Aproveite e se prepare com o Simulado do Beduka! Ele conta com questões das edições anteriores do Enem e é corrigido com base na nota TRI, a mesma do ENEM.
Nesse artigo você verá:
- Exercícios sobre Teorema de Tales;
- Resumo da matéria.
Faça os exercícios em um lugar tranquilo para conseguir se concentrar nos cálculos. Boa sorte!
Exercícios sobre Teorema de Tales
Baixe o melhor plano de estudos gratuito que você encontrará na internet.
1 – (MACK-SP) – Na figura, sendo a // b //c, o valor de x é:
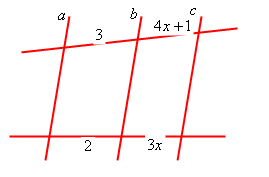
a) 3/2
b) 3
c) 4/3
d) 2
e) 1
2 – (PUC-MG) – Na figura, se AB = 3, AE = 700 e BC = 200, a medida de DB é:
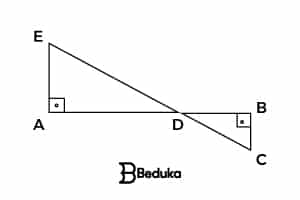
a) 1/3
b) 2/3
c) 4/3
d) 5/3
e) 7/3
3 – Enem – 2009 – A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metros. A distância em metros que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é
a) 1,16 metros.
b) 3,0 metros.
c) 5,4 metros.
d) 5,6 metros.
e) 7,04 metros.
4 – Cefet – O jardineiro Sr. Artur fez um canteiro triangular composto por folhagens e flores onde as divisões são todas paralelas à base.
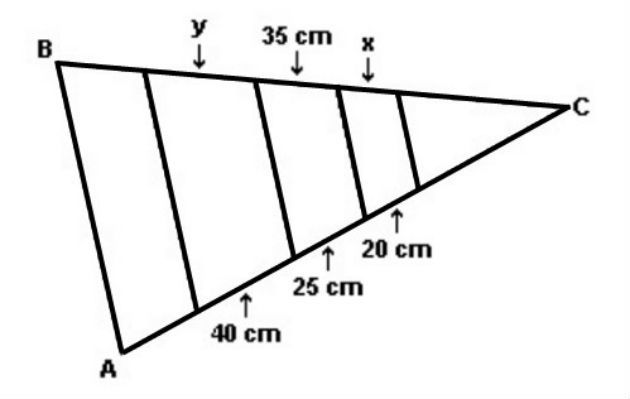
Sendo assim, as medidas x e y dos canteiros de flores são, respectivamente:
a) 30 cm e 50 cm.
b) 28 cm e 56 cm.
c) 50 cm e 30 cm.
d) 56 cm e 28 cm.
e) 40 cm e 20 cm.
5 – Cefet/MG – 2014 – Considere a figura em que
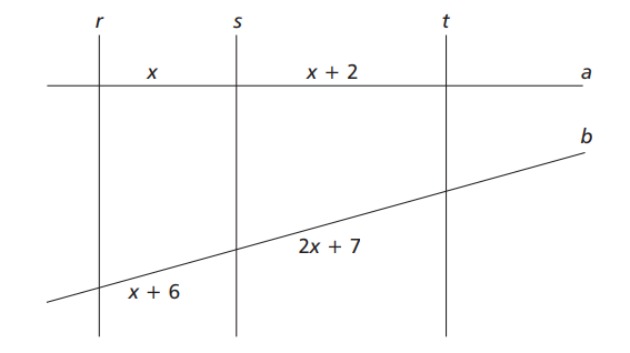
O valor de x é
a) 3.
b) 4.
c) 5.
d) 6.
6 – PUC/Campinas – 2007 – Na figura a seguir, as retas r, s e t são paralelas entre si
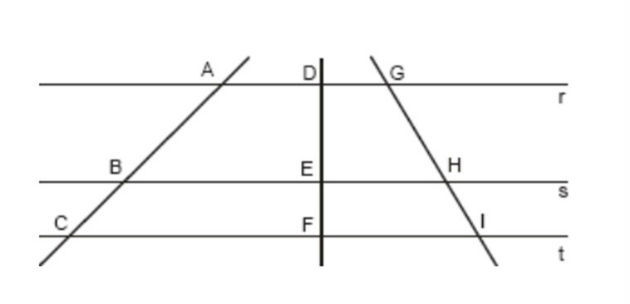
Se AC = x, BC = 8, DE = 15, EF = x – 10, GI = y e HI = 10, então x + y é um número
a) maior que 47
b) entre 41 e 46
c) menor que 43
d) quadrado perfeito
e) cubo perfeito
Agora confira as respostas com o gabarito abaixo.
Respostas dos Exercícios sobre Teorema de Tales
Exercício resolvido da questão 1 –
d) 2
Exercício resolvido da questão 2 –
b) 2/3
Exercício resolvido da questão 3 –
d) 5,6 metros.
Exercício resolvido da questão 4 –
b) 28 cm e 56 cm.
Exercício resolvido da questão 5 –
b) 4
Exercício resolvido da questão 6 –
b) entre 41 e 46
Gostou dos nossos Exercícios sobre Teorema de Tales? Compartilhe com os seus amigos e comente abaixo sobre áreas que você deseja mais explicações.
Aproveite e estude para o Enem com o Simulado Beduka. É gratuito!
Você foi bem nos exercícios sobre teorema de tales? Esperamos que sim! Mas se não tiver acertado todas as questões não tem problema, pois preparamos para você um resumo completo para entender toda matéria.
Resumo sobre Teorema de Tales
O Teorema de Tales afirma que quando duas retas são transversais a um feixe de retas paralelas, a divisão entre as medidas de dois segmentos quaisquer de uma delas é igual a divisão entre as medidas dos segmentos correspondente da outra reta.
OU SEJA, imagine um triângulo cortado por linhas retas. Teremos 4 partes, duas em cima e duas em baixo. A divisão de uma pela outra do lado direito é igual à divisão de uma pela outra do lado esquerdo.
Tales de Mileto era um filósofo, astrônomo e matemático nascido na Grécia, em 624 antes de Cristo. Ele foi extremamente importante para o desenvolvimento da matemática, no ramo da geometria. Um de seus estudos interessantes foi descobrir a altura de uma determinada pirâmide e relacionar a sombra de um objeto com a real altura dele.
Tales descobriu a altura da pirâmide por meio do tamanho da sombra formada por ela. Para isso, ele precisou fazer um experimento: pegou uma estaca e a colocou na areia. Assim que a sombra se formou, ele mediu o seu tamanho e o das pirâmides em um mesmo horário do dia. Deste modo, se formou a seguinte fórmula:
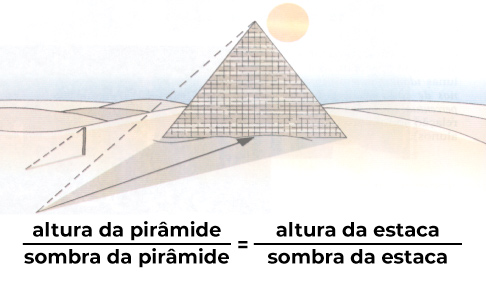
Então, Tales de Mileto desenvolveu a seguinte lei:
“Feixes de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes.”
Veja a seguir o esquema que representa o Teorema de Tales:
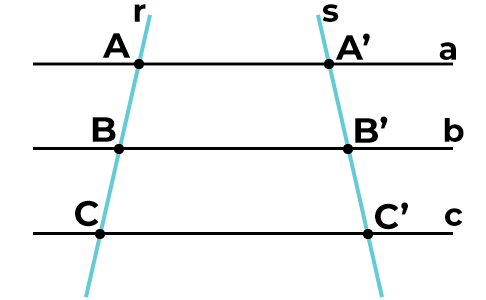
Podemos escrever esse Teorema da seguinte forma:
AB = A’B’
BC B’C’
Os segmentos são proporcionais quando um feixe de retas paralelas entre si, cortadas por duas transversais são formadas pela intersecção entre as retas paralelas e as transversais.
Teorema de Tales nos Triângulos
O Teorema de Tales pode ser utilizado também em cálculos que possuem triângulos, veja o exemplo:
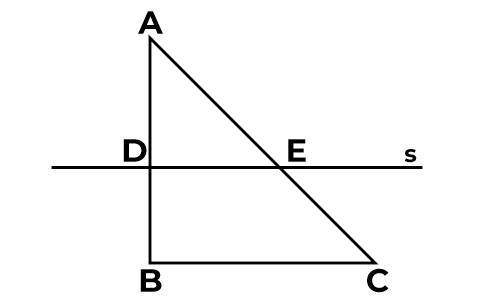
A partir da semelhança de triângulos, podemos concluir que o triângulo ABC é semelhante ao triângulo AED. Sendo assim, ele é representado da seguinte maneira:
Δ ABC ~ Δ AED
Gostou de aprender com nossos exercícios sobre Teorema de Tales? Não deixe de seguir o Beduka no Instagram para não perder nenhuma novidade!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!






7 Comentários
Olá, os exercícios aqui do site tem a resolução ou gabarito pra conferir as respostas?
Oi Camila, os exercícios possuem gabarito para você conferir as respostas, espero que tenha acertado!
Onde está o gabarito?
Oi, Ana! O Gabarito está logo abaixo das questões, contendo todas as respostas!
Oi, Ana! O gabarito está logo abaixo das questões, contendo todas as respostas. Espero que tenha acertado tudo!
Acredito que a resposta da questão 2 é 1/3 e não 2/3.
Como DB está no triângulo menor então também vai ter a parte menor. Assim, DB = 1/4 e AD = 2/3.
Fernanda, tudo bem? A resposta está correta mesmo. Como os triângulos ADE e BCD são semelhantes, pois seus ângulos são congruentes, seus lados correspondentes são proporcionais. Logo DB/AD = BC/AE. Ao calcularmos, vamos encontrar 2/3.