Muitos estudantes se assustam quando o assunto da aula de Física são os vetores, porém, com bastante atenção e dedicação é possível dominá-lo. Basta quais são as três grandezas básicas deles que tudo fica mais fácil.
Saber quais as características do vetor e como calculá-lo é bastante útil em diversas áreas da Física. Podemos encontrar vetores no cálculo da segunda lei de Newton ou na equação da força elétrica, por exemplo.
Por este motivo, para te ajudar a tirar de letra essa temática no Enem e demais vestibulares, fizemos este resumo completo. Bons estudos!
Preparamos este resumo para você entender quais as características do vetor. Vá direto ao conteúdo que deseja clicando em um dos tópicos abaixo:
- Quais as características do vetor?
- O que são os componentes de um vetor?
- Como calcular vetores?
- Regra do polígono
- Regra do paralelogramo
- Nós conectamos você à faculdade!
Você sabia que é possível entrar no curso dos seus sonhos sem precisar da nota do Enem? Com o Beduka Bolsas você garante desconto de até 65% na mensalidade + matrícula gratuita. Acesse agora mesmo!
Quais as características do vetor?
Um vetor pode ser definido como um segmento de reta que apresenta algumas propriedades básicas.
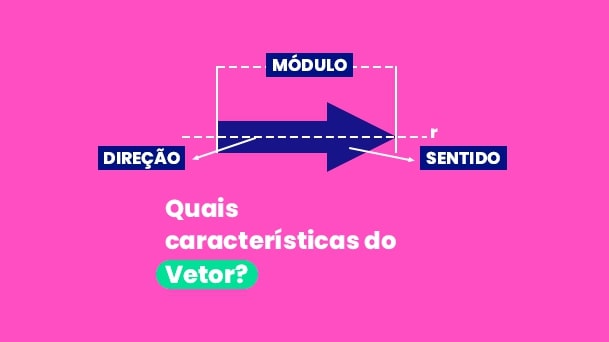
Essas propriedades estão presentes nas grandezas vetoriais (velocidade, aceleração, força, deslocamento, etc.) e são elas: o módulo, a direção e o sentido.
Conheça melhor quais as características do vetor:
- Módulo: é sempre um número real e positivo. Na representação gráfica, o comprimento do vetor corresponde ao módulo da grandeza que ele representa.
- Direção: é a reta suporte de um vetor que determina a sua direção.
- Sentido: é a orientação do segmento (ponta de seta) que indica o sentido do vetor.
A junção dessas três características define como determinada grandeza vetorial vai se comportar.
Para exemplificar as características do vetor, podemos utilizar a força peso em um corpo sobre uma superfície plana:
A direção do vetor é vertical, seu sentido é para baixo e seu módulo é igual à intensidade da força peso sobre ele.
Além disso, vale ressaltar que os vetores podem ser nomeados por uma letra qualquer, maiúscula ou minúscula, com uma seta sobre ela, indicando que representa uma grandeza vetorial.
O que são os componentes de um vetor?
Como os vetores estão localizados no espaço, precisamos de um sistema de coordenadas para sua definição e localização.
Geralmente, utilizamos o sistema de coordenadas cartesianas. Isso quer dizer que as coordenadas de um vetor dependem das componentes verticais e horizontais (componente y e componente x, respectivamente).
Conheça com detalhes os componentes de um vetor:
- Componente X: é a componente horizontal de um vetor. Se apontar para a direita, sua orientação é positiva. Se apontar para a esquerda, a orientação é negativa.
- Componente Y: é a componente vertical de um vetor. Se apontar para cima, seu sinal é positivo. Se apontar para baixo, seu sinal é negativo.
Depois de aprender quais as características do vetor e seus componentes, entenda como realizar as operações vetoriais.
Como calcular vetores?
Os cálculos que envolvem vetores não são realizados da mesma forma que as operações algébricas.
Os módulos de dois vetores são somados ou subtraídos somente se suas direções forem iguais.
Além disso, vale lembrar que a subtração é igual à soma com um vetor de mesmo módulo, mesma direção, mas de sentido oposto.
Entenda com mais detalhes a seguir:
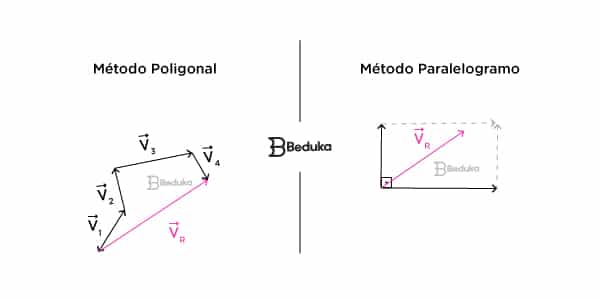
Regra do polígono
Essa regra é empregada na adição ou subtração de qualquer quantidade de vetores. Acompanhe o passo a passo:
- Junte os vetores, um pela origem e outro pela extremidade. Vá juntando conforme o número de vetores que você precisa somar ou subtrair.
- Em seguida, você deve traçar o vetor resultante.
- E por fim, você deve ligar a origem do primeiro com a extremidade do último, formando assim um polígono.
Regra do paralelogramo
Essa regra pode ser utilizada na adição ou subtração de apenas dois vetores. Veja como fazer:
- Coloque a origem dos dois vetores no mesmo ponto.
- Trace uma reta paralela a cada um passando pela extremidade do outro.
- O vetor resultante será o vetor que une a origem dos dois vetores com o cruzamento das duas retas paralelas a cada vetor, formando assim um paralelogramo.
Observação: para determinar o módulo do vetor soma obtido pelo método do paralelogramo, você deve utilizar a lei dos cossenos.
Coloque em prática o que aprendeu com nossa lista de exercícios sobre Vetores!
Esperamos que este resumo sobre quais as características do vetor tenha despertado em você a vontade de estudar mais sobre o incrível mundo da Física!
Logo abaixo temos uma oportunidade incrível para você, não deixe de conferir!
Nós conectamos você à faculdade!
O Beduka é o seu maior parceiro quando o assunto é entrar na faculdade. Aqui você encontra as melhores ferramentas para ficar mais perto do curso dos seus sonhos: resumos, listas de exercícios, simulado, teste vocacional, entre outras…
Mas sabe qual é a melhor de todas? O Beduka Bolsas!
O Beduka Bolsas é uma plataforma onde você pode comprar uma bolsa de estudos de até 65% de desconto e estudar em uma das melhores universidades do Brasil!
É isso mesmo! Temos mais de 90 opções de cursos para você escolher em 8 universidades parceiras.
Siga o Beduka no Pinterest e no Instagram e receba conteúdos gratuitos sobre o Enem e outros vestibulares todos os dias.
Obrigada por ler nosso artigo sobre quais as características do vetor.