O determinante é o número ligado a uma matriz quadrada. Leia todo o resumo sobre essa matéria e teste seus conhecimentos com os exercícios de determinantes.
O determinante é uma das matérias que mais causam dúvidas nos estudantes, por isso resolvemos esclarecer algumas questões nesse artigo. Na prova do ENEM, no caderno de Matemática e suas Tecnologias podem ser cobrados alguns exercícios sobre determinantes.
Resumo – Determinantes
Na matemática, o determinante permite transformar a matriz em um número real.
Os cálculos realizados entre os elementos de uma matriz quadrada estão relacionados ao número chamado determinante da matriz.
O det A é o determinante da matriz A e os parênteses, colchetes e até mesmo as barras duplas são substituídas por barras simples. Para entender melhor vamos analisar o seguinte exemplo:
Matriz A =

Essa matriz pode ser ser representada por colchetes ou barras duplicadas, sendo então det A =

Nas matrizes quadradas, onde possui ordem 3×3 os cálculos podem ser feitos repetindo a 1ª e a 2ª coluna e multiplicar os elementos do determinantes, assim realizar a regra de Sarrus.
Lembrando que uma matriz é quadrada quando o número de linhas é igual ao número de colunas.
Veja o exemplo de um determinante de ordem 3×3:
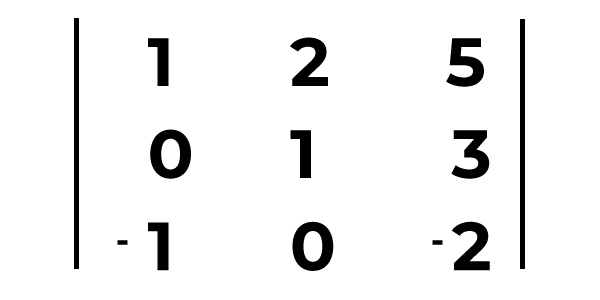
Aplicando a Regra de Sarrus temos:
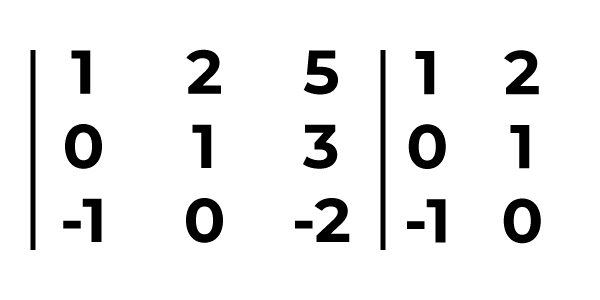
Multiplicando os números de acordo com a seta temos:
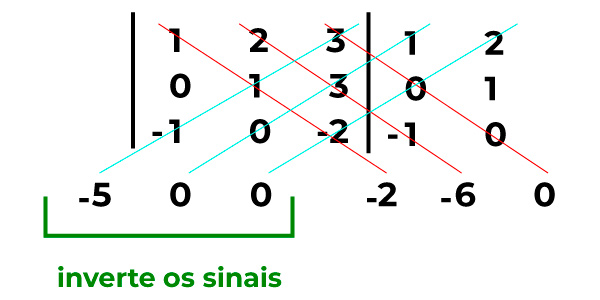
Depois de calculado é necessário inverter os sinais das diagonais secundárias, então será +5, 0, 0, – 2, -6, 0.
Já em uma matriz de ordem 2×2, cada diagonal é multiplicado e assim se realiza a subtração do produto da diagonal principal do produto da diagonal secundária.
Faça os exercícios de determinantes para testar seus conhecimentos sobre o assunto.
Exercícios de Determinantes
Baixe o melhor plano de estudos gratuito que você encontrará na internet.
1 – (Vunesp) – Dadas as matrizes A =
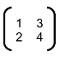
e B =
o determinante da matriz A.B é:
a) – 1
b) 6
c) 10
d) 12
e) 14
2 – (UESP) – Se o determinante da matriz
p 2 2
p 4 4
p 4 1
é igual a -18, então o determinante da matriz
p -1 2
p -2 4
p -2 1
é igual a:
a) -9
b) -6
c) 3
d) 6
e) 9
3 – (UESP) – Se o determinante da matriz:
2 1 0
k k k
1 2 -2
é igual a 10, então o determinante da matriz:
2 1 0
k+4 k+3 k-1
1 2 -2
é igual a:
a) 7
b) 8
c) 9
d) 10
e) 11
4 – (Funcab) – Sabendo que A é uma matriz quadrada de ordem 3 e que o determinante de A é -2, calcule o valor do determinante da matriz 3A.
a) – 8
b) – 54
c) 27
d) 18
e) – 2
5 – (Funcab) – Considerando a matriz quadrada A abaixo, e det(A) seu determinante, calcule o valor de 5.det(A).
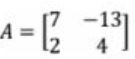
a) 10
b) -140
c) 270
d) 130
e) -35
6 – (PM PR 2010 – Cops) – Considere uma colisão de dois veículos. Num sistema de coordenadas cartesianas, as posições finais destes veículos após a colisão são dadas nos pontos A = (2,2) e B = (4, 1). Para compreender como ocorreu a colisão é importante determinar a trajetória retilínea que passa pelos pontos A e B.
Essa trajetória é dada pela equação:
a) x – y = 0
b) x + y – 5 = 0
c) x – 2y + 2 = 0
d) 2x + 2y – 8 = 0
e) x + 2y – 6 = 0
7 – (RFB 2009 – Esaf) – Com relação ao sistema
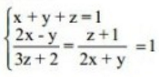
onde
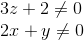
pode-se, com certeza, afirmar que:
a) é impossível
b) é indeterminado
c) possui determinante igual a 4
d) possui apenas a solução trivial
e) é homogêneo
8 – (ANAC – ESAF 2016) – Dada a matriz A abaixo, o determinante da matriz 2A é igual a:
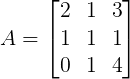
a) 40.
b) 10.
c) 18.
d) 16.
e) 36.
Respostas dos Exercícios de Determinantes
Exercício resolvido da questão 1 –
e) 14
Exercício resolvido da questão 2 –
e) 9
Exercício resolvido da questão 3 –
b) 8
Exercício resolvido da questão 4 –
b) – 54
Exercício resolvido da questão 5 –
c) 270
Exercício resolvido da questão 6 –
e) x + 2y – 6 = 0
Exercício resolvido da questão 7 –
c) possui determinante igual a 4
Exercício resolvido da questão 8 –
a) 40.
Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos exercícios de determinantes? Compartilhe com os seus amigos e comente abaixo sobre áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





