Os 9 Melhores Exercícios de Área e Perímetro com Gabarito

Área e perímetro são medidas dos elementos das figuras geométricas. A área mede a superfície de uma figura plana (base vezes altura) enquanto o perímetro mede seu contorno (soma dos lados). Leia nosso Resumo e faça os Exercícios de Área e Perímetro.

Quando você terminar as Questões sobre Área e Perímetro, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil. 

O ser humano inventou algumas formas de conseguir simbolizar, esquematizar e ler a realidade. A matemática foi uma delas. 

Imagine que uma pessoa vá construir um prédio. Ela precisa saber alguns dados como o tamanho do local, seu contorno, a temperatura que faz normalmente naquela região, umidade, características do solo e muito mais.

Dois dos dados mais fundamentais para qualquer leitura de um terreno são o perímetro e a área.

Eles te mostram o contorno de uma região (perímetro) e o espaço ocupado por ela (área). 

Vamos então ver, neste artigo, essas duas informações essenciais para qualquer exercício de Geometria Plana.

• Você é uma daquelas pessoas que tem sede de conhecimento? Então siga o Instagram do Beduka para conteúdos diários.

O que são a Área e o Perímetro?

Área e perímetro são medidas dos elementos das figuras geométricas. A área mede a superfície de uma figura plana (base vezes altura) enquanto o perímetro mede seu contorno (soma dos lados).

• Quer conhecer ainda mais profundamente sobre o tema? Então leia nosso Artigo Completo sobre Área, Perímetro e Volume.

O que é a Área?

A área de uma figura é a medida da sua superfície. Usamos a área para falar primeiro das formas planas; aquelas que possuem duas dimensões (largura e altura). Podemos dizer que é o preenchimento de uma figura plana.

Ao recortar uma figura em vários quadradinhos muito pequenos, percebemos que cada quadrado desse equivale a uma “unidade de área”. Dessa forma, somados, preenchem a área de uma figura.

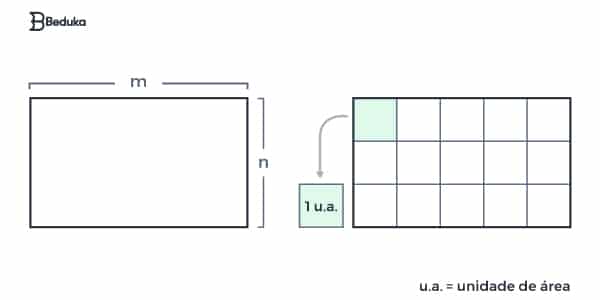
Imagine uma folha de papel que foi pintada integralmente por uma tinta verde. Pois bem, onde estiver pintado de verde, equivale à área da figura.

A área também pode ser calculada em objetos volumosos, neste caso, ela se dá pela soma das áreas da superfície do objeto (área total).

Como calcular a área?

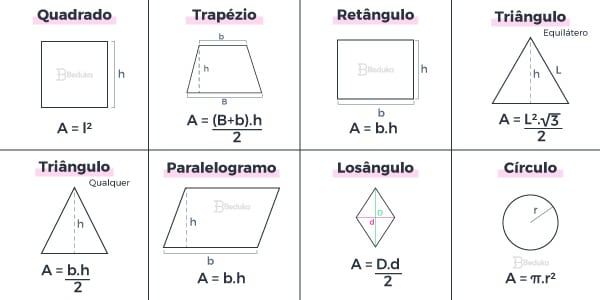
Para calcular a área de uma superfície, o comum é multiplicar o valor da base (b) pela altura (h) do objeto. Algumas figuras, como os triângulos e os círculos, têm fórmulas próprias. 

Outras figuras como os polígonos de 5 lados ou mais, podem ser divididas em triângulos. Assim, calculamos as áreas dos triângulos, somamos e achamos a do polígono final!

Veja um resumo de fórmulas para calcular áreas a seguir:

As unidades de medida utilizadas para área são:

km²: quilômetro quadrado;

hm²: hectômetro quadrado;

dam²: decâmetro quadrado;

m²: metro quadrado;

dm²: decímetro quadrado;

cm²: centímetro quadrado;

mm²: milímetro quadrado.

• Que tal aproveitar para fazer Exercícios de Geometria Plana?

Como calcular perímetro?

O Perímetro é o valor do contorno de uma figura, seja plana, espacial ou até mesmo não geométrica. É mais comum ser pedido na geometria plana, mas pode acontecer de cair em uma questão espacial.

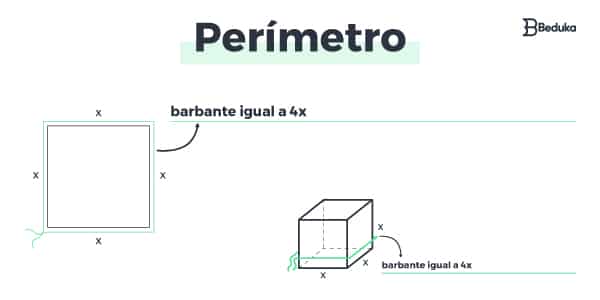
Como calcular o perímetro em quadriláteros?

2(b + h)

Ela corresponde à soma de duas vezes a base (b) e a altura (h), resultando em 2b + 2h.

Como calcular o perímetro em círculos?

C = 2.π.r

Sendo:

π = 3,14159265

C = Perímetro ou comprimento da circunferência

r = raio interno da circunferência

• Aproveite a oportunidade e faça As 10 Melhores Questões de Matemática do ENEM

Exercícios de Área e Perímetro com Gabarito

Esperamos que, com esse resumo, tudo tenha ficado mais claro para você. 

Parabéns por ter lido até aqui!

Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.

Questão 1 – (PUC-RIO 2009) Calcule a área do triângulo de vértices A = (1,2), B = (2,4) e C = (4,1).

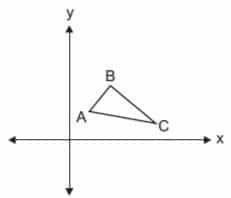
a) 5/2

b) 3

c) 7/2

d) 4

e) 9/2

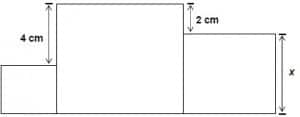
Questão 2 – (PUC RIO 2008) A área da figura abaixo é:

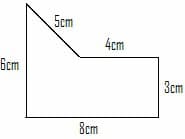
a) 30 m²

b) 33 cm²

c) 36 cm²

d) 48 cm²

Questão 3 – (PUC RIO 2008) Um festival foi realizado num campo de 240 m por 45 m. Sabendo que por cada 2 m² havia, em média, 7 pessoas, quantas pessoas havia no festival?

a) 42.007

b) 41.932

c) 37.800

d) 24.045

e) 10.000

Questão 4 – (PUC-RIO 2007) A hipotenusa de um triângulo retângulo mede 10 cm e o perímetro mede 22 cm. A área do triângulo (em cm²) é:

a) 50

b) 4

c) 11

d) 15

e) 7

• Muito bem! Você chegou à metade dos Exercícios de Área e Perímetro.

Questão 5 – (PUC-RIO 2007) Num retângulo de perímetro 60, a base é duas vezes a altura. Então a área é:

a) 200

b) 300

c) 100

d) 50

e) 30

Questão 6 – (UDESC 2010) O projeto de uma casa é apresentado em forma retangular e dividido em quatro cômodos, também retangulares, conforme ilustra a figura.

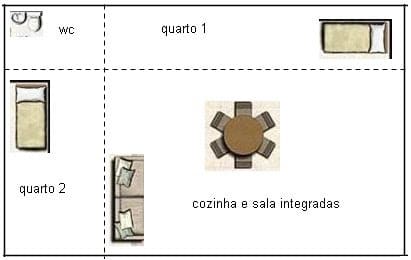
Sabendo que a área do banheiro (wc) é igual a 3m² e que as áreas dos quartos 1 e 2 são, respectivamente, 9m² e 8m², então a área total do projeto desta casa, em metros quadrados, é igual a:

a) 24

b) 32

c) 44

d) 72

e) 56

Questão 7 – (UFMG 2008) O octógono regular de vértices ABCDEFGH, cujos lados medem 1 dm cada um, está inscrito no quadrado de vértices PQRS, conforme mostrado nesta figura:

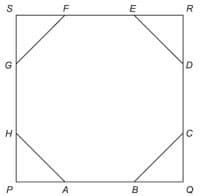
Então, é CORRETO afirmar que a área do quadrado PQRS é:

a) 1 + 2√2 dm²

b) 1 + √2 dm²

c) 3 + 2√2 dm²

d) 3 + √2 dm²

• Ufa, estamos quase lá! Faça os 2 últimos Exercícios de Área e Perímetro.

Questão 8 – (FUVEST 2009) A figura representa sete hexágonos regulares de lado 1 e um hexágono maior, cujos vértices coincidem com os centros de seis dos hexágonos menores. Então, a área do pentágono pintada é igual a:

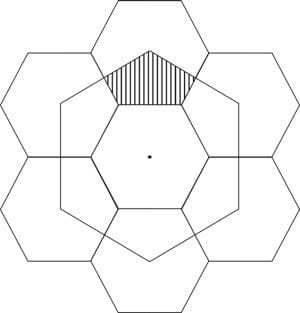
a) 3√3

b) 2√3

c) (3√3)/2

d) √3

e) (√3)/2

Questão 9 – (UFPR 2010) A soma das áreas dos três quadrados ao lado é igual a 83 cm². Qual é a área do quadrado maior?

a) 36 cm²

b) 20 cm²

c) 49 cm²

d) 42 cm²

e) 64 cm²

• Parabéns, você fez todas as Questões de Área e Perímetro, Confira agora o Gabarito:

Gabarito das Exercícios de Área e Perímetro

Exercício resolvido da questão 1 –

Alternativa correta: c) 7/2

Exercício resolvido da questão 2 –

Alternativa correta: a) 30 cm²

Exercício resolvido da questão 3 –

Alternativa correta: c) 37.800

Exercício resolvido da questão 4 –

Alternativa correta: c) 11

Exercício resolvido da questão 5 –

Alternativa correta: a) 200

Exercício resolvido da questão 6 –

Alternativa correta: c) 44

Exercício resolvido da questão 7 –

Alternativa correta: c) 3 + 2√2 dm²

Exercício resolvido da questão 8 –

Alternativa correta: e) (√3)/2

Exercício resolvido da questão 9 –

Alternativa correta: c) 49 cm²

Estude para o Enem com o Simulado Beduka. É gratuito!

Gostou dos nossos Exercícios de Área e Perímetro? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.