Os 10 melhores exercícios de interpretação de problemas matemáticos com o Gabarito!

Você sabia que interpretar exercícios é uma arte? Pois é, a palavra “arte” significa “técnica”… E isso explica porque muitos alunos acham as questões tão confusas! Para te ajudar, fizemos um resumo ensinando essa habilidade. Depois, você pode treinar com os exercícios de interpretação de problemas matemáticos!

Quer seguir diretamente para alguma parte? Clique em um dos tópicos abaixo:

• Só conseguimos dominar aquilo que conhecemos!
• Como interpretamos as questões de matemática?
• Domine a interpretação de problemas em 4 passos
• Lista com os 10 melhores exercícios de interpretação de problemas matemáticos!
• Gabarito dos exercícios sobre interpretação de problemas matemáticos.

Não sabe como organizar seus estudos? Apresentamos o Plano de Estudos Beduka! Com ele, você conseguirá adequar a sua rotina ao seu tempo de aprendizado.

Só conseguimos dominar aquilo que conhecemos!

Você já entendeu que vamos fazer algo literalmente artístico aqui, já que precisamos de muita habilidade para interpretar as questões! 

(Não é atoa que chamamos de problemas matemáticos…hahaha)

Porém, a técnica é a parte prática da coisa, ela é a ação que vamos fazer ao se deparar com uma questão. 

Então, a primeira coisa que precisamos fazer é conhecer os elementos de um enunciado. Depois saberemos o que fazer com ele!

Vamos analisar os seus 4 componentes:

1. A situação-problema

Como o próprio nome diz, a situação-problema é o contexto que estamos lidando. Ele narra qual é o fato que aconteceu e que levou o problema a ser resolvido.

Basicamente, existem dois tipos de problemas:

• Problemas de determinação: precisamos descobrir a informação que falta.
• Problemas de demonstração: temos de mostrar que uma afirmativa da matemática é verdadeira.

2. Os dados

Os dados são justamente as informações que usamos na hora de resolver o problema. Essas informações podem ser números ou palavras, podem estar explícitas ou implícitas.

3. O Objetivo

Como você já sabe, o objetivo é onde queremos chegar. Ele é aquilo que procuramos e, quando acharmos, será dado como resposta da questão. 

• São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

4. As operações

As operações são as ações matemáticas que faremos para resolver a questão. São nelas que usamos os dados e calculamos o que precisamos.

Preste atenção! Essa é uma etapa essencial, pois precisamos identificar quais operações são necessárias em cada situação-problema. Esse é o caminho para o sucesso!

E é aqui que entra a estrela da noite: a interpretação de texto!

Vamos falar sobre a interpretação de texto para depois terminar de resolver esse problema.

Como interpretar as questões de matemática?

Saber as fórmulas é importantíssimo, mas não se resume a isso. Somente a interpretação faz com que nossa cabeça saiba a hora certa de usar a fórmula e com quais informações.

Uma boa palavra para entender a interpretação é “tradução”. Nós precisamos traduzir a linguagem matemática para o português e vice-versa.

Por isso, podemos afirmar que o sucesso na solução de problemas está ligado à habilidade (arte) de enxergar a ligação das palavras do português com a sua representação na matemática.

Com base nisso, separamos algumas dicas para fazer essa tradução de forma correta. 

Observe:

• A preposição “de” e suas contrações indicam uma multiplicação se estiverem entre duas quantidades. Isso acontece muito nas questões de Porcentagem. 
• No caso da Probabilidade, será a partícula “e” entre eventos que indica multiplicação. Quando houver “ou”, significa soma.
• Se a preposição “por”  estiver entre duas quantidades, ela representará uma divisão. Há outros termos que são comuns, como: “razão” ou “quociente”. Algumas questões vêm falando claramente: “Fulana dividiu …”

• Quando os verbos “é”, “possui”, “tem” e “equivale” estão entre duas quantidades, eles nos apontam para uma equação. Elas podem envolver incógnitas ou não.
• De modo geral, a presença de uma incógnita pode ser identificada pelas palavras: qual, que, certo valor, certa quantia, quantos…

Este é apenas um resumo simples, mas já fizemos um artigo COMPLETO sobre interpretação de problemas matemáticos. Nele, você confere outras dicas mais detalhadas, com exemplos de cada uma e tudo o mais!

Exemplo resolvido em 4 passos!

Bom, agora que já entendemos todos os elementos do enunciado e as estratégias de interpretação, podemos resolver o nosso exemplo:

“O perímetro de um triângulo retângulo é 12 cm. As medidas de seus lados são números consecutivos. Qual é a medida da área dessa figura?”

Como você resolveria esse problema?

Basta seguir os 4 passos:

• 1º Passo: leia o problema marcando as partes importantes (dados e objetivo);
• 2º Passo: anote e organize o que é dado;
• 3° Passo: olhe para as anotações, veja quais operações podem ser feitas e quantas etapas precisará para isso (interpretação);
• 4° Passo: resolva todas as etapas e veja se o resultado final corresponde ao objetivo.

Solução:

Vamos chamar de “x” o lado menor do triângulo. Se os lados são números consecutivos, então o lado mediano é “x+1” e o lado maior é “x+2”. 

Sabemos que perímetro é a soma dos lados, então x+x+1+x+2 = 12. Resolvendo a equação, temos: 3x+3 = 12 // 3x = 9 // x = 3.

Note que 3 é o valor do lado menor, então o outro mede 4 e o maior mede 5. Se foi dito que é um triângulo retângulo, então 5 é a hipotenusa. Logo, os valores que sobram para os catetos são 3 e 4.

Aqui não importa saber a ordem em que eles estão, o importante é notar que eles serão a base e a altura do triângulo. É exatamente disso que precisamos para usar a fórmula de área!

Aplicando a fórmula (b.h)/2, temos: (3.4)/2 = 12/2 = 6.

Agora sim resolvemos o problema: o valor de sua área é 6!

Os 10 exercícios de interpretação de problemas matemáticos!

Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.

Obrigado por ter lido até aqui!

Quando acabar de resolver as atividades, estude para o Enem com o Simulado Beduka. É gratuito e pode ser personalizado com as matérias que você quiser!

Questão 1- (Beduka)

Carla tem 2 reais a mais que Paula, Paula tem dois reais a mais que Leia e Leia tem dois reais a mais que Vivian. As 4 juntas possuem 48 reais. Quanto cada uma tem individualmente?

a) Carla tem 14, Paula tem 12, Leila tem 10 e Vivian tem 8.

b) Vivian tem 8, Leila tem 10, Paula tem 12 e Carla tem 14.

c) Carla tem 9, Paula tem 11, Leila tem 13 e Vivian tem 15.

d) Carla tem 10, Paula tem 12, Leila tem 14 e Vivian tem 16.

e) Vivian tem 9, Leila tem 11, Paula tem 13 e Carla tem 15.

Questão 2- (Enem 2012)

Um maquinista de trem ganha R$ 100,00 por viagem e só pode viajar a cada 4 dias. Ele ganha somente se fizer a viagem e sabe que estará de férias de 1º a 10 de junho, quando não poderá viajar. Sua primeira viagem ocorreu no dia primeiro de janeiro. Considere que o ano tem 365 dias.

Se o maquinista quiser ganhar o máximo possível, quantas viagens precisará fazer? 

a) 37.

b) 51.

c) 88.

d) 89.

e) 91.

• Já chegamos a 20% dos exercícios de interpretação de problemas matemáticos. Vamos lá!

Questão 3- (Beduka)

Em um congresso há 50 homens e 30 mulheres. Quantas comissões de 6 pessoas podemos formar, obedecendo a condição de que cada uma tenha 4 mulheres e 2 homens?

a) 300 500 199 possibilidades de comissões.

b) 33 571 125 possibilidades de comissões.

c) 27 405 possibilidades de comissões.

d) 28 630 possibilidades de comissões.

e) 1225 possibilidades de comissões.

Questão 4- (PUC – RJ) 

3/5 de um número somados a ½ é igual a 2/3 desse mesmo número. Indique a opção que apresenta esse número.

a) 0.

b) 1.

c) 20/33.

d) 33/20.

e) 15/2.

Questão 5- (Detran SP – Vunesp) 

O gráfico apresenta a distribuição de vítimas de trânsito no mês de julho de 2013, segundo o tipo de usuário da via pública em uma determinada cidade brasileira.

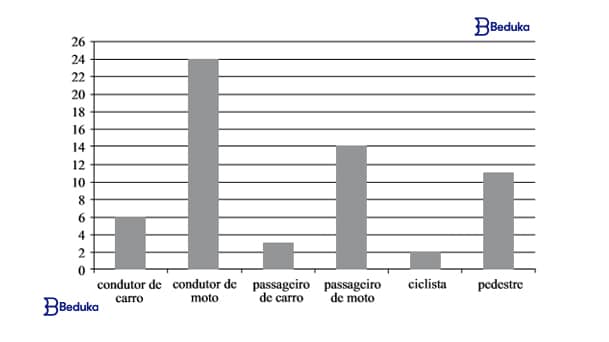
O grupo que corresponde a 2/5 do total de vítimas é o de

a) passageiro de carro.

b) condutor de carro.

c) passageiro de moto.

d) pedestre.

e) condutor de moto.

• Você já chegou à metade das questões de interpretação de problemas matemáticos. Não pare agora!

Questão 6- (Enem/2012) 

O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existam 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa.

O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido. Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta.

As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.

O diretor sabe que algum aluno acertará a resposta porque há:

a) 10 alunos a mais do que possíveis respostas distintas.

b) 20 alunos a mais do que possíveis respostas distintas.

c) 119 alunos a mais do que possíveis respostas distintas.

d) 260 alunos a mais do que possíveis respostas distintas.

e) 270 alunos a mais do que possíveis respostas distintas.

Questão 7- (CEFET/MG – 2018) 

Numa família com 7 filhos, sou o caçula e 14 anos mais novo que o primogênito de minha mãe. Dentre os filhos, o quarto tem a terça parte da idade do irmão mais velho, acrescidos de 7 anos. Se a soma de nossas três idades é 42, então minha idade é um número

a) divisível por 5.

b) divisível por 3.

c) primo.

d) par.

Questão 8- (Unifor–CE – adaptada)

José ganhou um prêmio no valor de R$ 5.000,00 e dividiu-o entre seus três filhos da seguinte forma: Pedro recebeu R$300,00 a menos que João, que, por sua vez, recebeu R$ 100,00 a mais que Antônio. A quantia recebida por Pedro foi:

a) R$1.500,00.

b) R$2.500,00.

c) R$1.000,00.

d) R$500,00.

• Ufa! Só faltam mais dois exercícios sobre interpretação de problemas matemáticos. Continue!

Questão 9- (FUVEST 2020)

A dona de uma lanchonete observou que, vendendo um combo a R$ 10,00, 200 deles são vendidos por dia, e que, para cada redução de R$ 1,00 nesse preço, ela vende 100 combos a mais. Nessas condições, qual é a máxima arrecadação diária que ela espera obter com a venda desse combo?

a) R$ 2.000,00.

b) R$ 3.200,00.

c) R$ 3.600,00.

d) R$ 4.000,00.

e) R$ 4.800,00.

Questão 10- (ENEM)

Três alunos, X, Y e Z, estão matriculados em um curso de inglês. Para avaliar esses alunos, o professor optou por fazer cinco provas. Para que seja aprovado nesse curso, o aluno deverá ter a média aritmética das notas das cinco provas maior ou igual a 6. Na tabela, estão dispostas as notas que cada aluno tirou em cada prova.

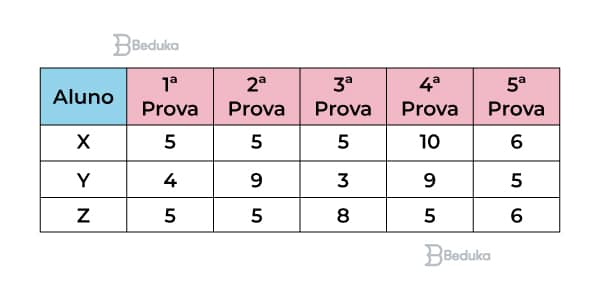
Com base nos dados da tabela e nas informações dadas, ficará(ão) reprovado(s)

a) apenas o aluno Y.

b) apenas o aluno Z.

c) apenas os alunos X e Y.

d) apenas os alunos X e Z.

e) os alunos X, Y e Z.

• Parabéns, você fez todos os exercícios de interpretação de problemas matemáticos. Confira agora o Gabarito:

Gabarito das questões sobre interpretação de problemas matemáticos

Exercício resolvido da questão 1 –

Alternativa correta: e) Vivian tem 9, Leila tem 11, Paula tem 13 e Carla tem 15.

Exercício resolvido da questão 2 –

Alternativa correta: c) 88.

Exercício resolvido da questão 3 –

Alternativa correta: b) 33 571 125 possibilidades de comissões.

Exercício resolvido da questão 4 –

Alternativa correta: e) 15/2.

Exercício resolvido da questão 5 –

Alternativa correta: e) condutor de moto.

Exercício resolvido da questão 6 –

Alternativa correta: a) 10 alunos a mais do que possíveis respostas distintas.

Exercício resolvido da questão 7 –

Alternativa correta: c) primo.

Exercício resolvido da questão 8 –

Alternativa correta: a) R$1.500,00.

Exercício resolvido da questão 9 –

Alternativa correta: c) R$ 3.600,00.

Exercício resolvido da questão 10 –

Alternativa correta: b) apenas o aluno Z.

Gostou dos nossos exercícios de interpretação de problemas matemáticos? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.