Um sistema de equações é formado por um conjunto de expressões que possuem mais de uma incógnita. Para resolver um sistema é necessário encontrar os valores que satisfaçam simultaneamente todas as equações. Leia nosso resumo e faça Os Exercícios de Sistemas de Equações.
Quando você terminar os Exercícios de Sistemas de Equações, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil.
As equações são igualdades entre duas expressões matemáticas e se validam através de determinados valores das variáveis.
As variáveis são valores não definidos previamente representados por letras. Essas variáveis também podem ser chamadas de incógnitas quando representam exatamente um número desconhecido, mas que, quando descoberto, soluciona a equação.
Sendo assim, um sistema de equações é formado por um conjunto de igualdades entre duas expressões matemáticas.
Vamos entender melhor tudo isso? Então continue lendo o artigo até o final.
O que é Sistema de Equação? (Sistema Linear)
Também conhecido como sistema linear, o sistema de equações é formado por um conjunto de expressões que possuem mais de uma incógnita. Geralmente, recorremos a ele quando precisamos resolver problemas matemáticos que necessitam que sejam consideradas mais de uma equação ao mesmo tempo.
Como resolver um Sistema de Equação? (1° grau)
Existem dois métodos para resolver um Sistema de Equação do Primeiro Grau, o método da substituição e o método da soma. Veremos esses dois a seguir.
- Tudo o que você precisa saber sobre Equação do 1° grau.
Método da substituição
Esse método consiste em escolher uma das equações e isolarmos uma das incógnitas para determinar o seu valor em relação à outra incógnita.
Logo após, substituímos esse valor na outra equação.
Assim sendo, a segunda equação ficará com uma única incógnita e, por isso, poderemos encontrar o seu valor final.
Para finalizar, substituímos na primeira equação o valor encontrado e, assim, encontramos também o valor da outra incógnita. Vamos ver isso em um exemplo:
Observe este sistema:

Método da Adição
O método da adição é um dos modos mais conhecidos de resolver sistemas lineares com duas equações e duas incógnitas. Esse método consiste em somar as equações de um sistema termo a termo.
Para resolver um sistema linear através do método da adição, precisamos lembrar que os coeficientes de uma das incógnitas deve ser oposto, ou seja, ter números iguais com sinais contrários ao outro correspondente na outra equação.
Caso o sistema já não esteja assim, precisamos multiplicar todos os termos de uma das equações por um número que coloque o sistema na situação explicada anteriormente.
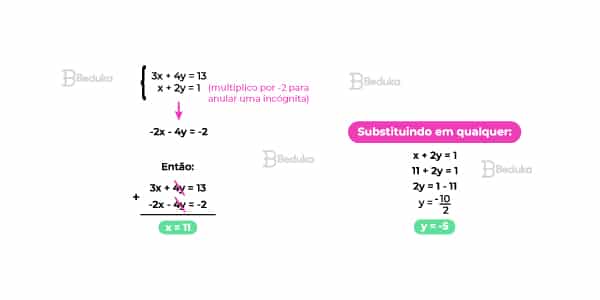
Assim sendo, será possível simplificar as equações e encontrar a solução da questão. Observe isso sendo feito na prática:
Quais as classificações de um sistema de equações?
Podemos classificar um sistema linear quanto ao número de soluções. Um sistema linear pode ser classificado em possível e determinado, possível e indeterminado e impossível.
- Sistema é possível e determinado (SPD): solução única;
- Sistema possível e indeterminado (SPI): mais de uma solução;
- Sistema impossível: não admite solução.
Aproveite para conferir também Os Exercícios de Equação do Segundo Grau.
Exercícios de sistemas de equações com Gabarito
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Obrigado por ter lido até aqui!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1 – (Fuvest) Um supermercado adquiriu detergentes nos aromas limão e coco. A compra foi entregue, embalada em 10 caixas, com 24 frascos em cada caixa. Sabendo-se que cada caixa continha 2 frascos de detergentes a mais no aroma limão do que no aroma coco, o número de frascos entregues, no aroma limão, foi:
a) 110
b) 120
c) 130
d) 140
e) 150
Questão 2 – (Vunesp) Em um campeonato de futsal, se um time vence, marca 3 pontos; se empata, marca 1 ponto e se perde não marca nenhum ponto. Admita que, nesse campeonato, o time A tenha participado de 16 jogos e perdido apenas dois jogos. Se o time A, nesses jogos, obteve 24 pontos, então a diferença entre o número de jogos que o time A venceu e o número de jogos que empatou, nessa ordem, é
a) 8.
b) 4.
c) 0.
e) – 8.
d) – 4.
Questão 3 – (VUNESP) Maria tem em sua bolsa R$15,60 em moedas de R$ 0,10 e de R$ 0,25. Dado que o número de moedas de 25 centavos é o dobro do número de moedas de 10 centavos, o total de moedas na bolsa é:
a) 68.
b) 75.
c) 78.
d) 81.
e) 84.
Questão 4 – (UNIFESP) Numa determinada livraria, a soma dos preços de aquisição de dois lápis e um estojo é R$10,00. O preço do estojo é R$5,00 mais barato que o preço de três lápis. A soma dos preços de aquisição de um estojo e de um lápis é:
a) R$3,00.
b) R$6,00.
c) R$12,00.
d) R$4,00.
e) R$7,00.
- Muito bem! Você chegou à metade dos Exercícios de Sistemas de Equações.
Questão 5 – (Cefet RJ) Uma garrafa PET (politereftalato de etileno) com sua tampa custa sessenta centavos. Sabendo que a garrafa custa cinquenta centavos a mais que a tampa, quanto custa só a tampa?
a) R$ 0,05
b) R$ 0,15
c) R$ 0,25
d) R$ 0,35
Questão 6 – (Cefet RJ)
Se eu leio 5 páginas por dia de um livro, eu termino de ler 16 dias antes do que se eu estivesse lendo 3 páginas por dia. Quantas páginas tem o livro?
a) 120
b) 125
c) 130
d) 135
- Ufa, estamos quase lá! Faça os 3 últimos Exercícios de Sistemas de Equações
Questão 7 – (Uerj 2015)

De acordo com os dados do quadrinho, a personagem gastou R$ 67,00 na compra de x lotes de maçã, y melões e quatro dúzias de bananas, em um total de 89 unidades de frutas.
Desse total, o número de unidades de maçãs comprado foi igual a:
a) 24
b) 30
c) 36
d) 42
Questão 8 – (Vunesp) Uma lapiseira, três cadernos e uma caneta custam, juntos, 33 reais. Duas lapiseiras, sete cadernos e duas canetas custam, juntos, 76 reais. O custo de uma lapiseira, um caderno e uma caneta, juntos, em reais é:
a) 11
b) 12
c) 13
d) 17
e) 38
- Parabéns, você fez todos Exercícios de Sistemas de Equações, Confira agora o Gabarito:
Gabarito dos Exercícios de Sistemas de Equações
Exercício resolvido da questão 1 –
Alternativa correta:c) 130
Exercício resolvido da questão 2 –
Alternativa correta: d) – 4.
Exercício resolvido da questão 3 –
Alternativa correta: c) 78.
Exercício resolvido da questão 4 –
Alternativa correta: e) R$7,00.
Exercício resolvido da questão 5 –
Alternativa correta: a) R$ 0,05
Exercício resolvido da questão 6 –
Alternativa correta: a) 120
Exercício resolvido da questão 7 –
Alternativa correta: c) 36
Exercício resolvido da questão 8 –
Estude para o Enem com o Simulado Beduka. É gratuito!
Alternativa correta: c) 13
Gostou dos nossos Exercícios de Sistemas de Equações? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.






1 Comentário
A respeito do primeiro exemplo teve um erro na operação.