Seja para treinar com exercícios de tronco de pirâmide ou só para consultar as fórmulas de Área e Volume, nós podemos te ajudar! A seguir, você confere um resumo seguido pelas 10 melhores questões de tronco de pirâmide. O gabarito te espera ao final.
Se quiser ir direto a algum ponto, você pode clicar em um dos tópicos abaixo:
- De onde veio o tronco de pirâmide?
- Quais são os elementos do tronco de pirâmide?
- Como calcular a área de um tronco de pirâmide?
- Qual o volume de um tronco de pirâmide?
- Exercícios sobre tronco de pirâmide
- Gabarito das questões sobre tronco de pirâmide
Faça um ótimo proveito do conteúdo e lembre-se de que é preciso treinar aquilo que aprendemos. Por isso temos o Simulado Gratuito do Beduka, que é online e personalizável!
O que é um tronco de pirâmide e de onde ele vem?
Pelo próprio nome desse sólido já fica claro que ele veio de uma Pirâmide, portanto, é uma parte dela.
Para entender como chegamos até aqui, imagine que pegamos a pirâmide e fizemos cortes. A secção transversal é o corte que fazemos como se passasse uma faca no meio dela, cortando horizontalmente.
Dessa forma, nós vamos ter duas partes. A de cima, com a pontinha da pirâmide, forma uma outra mini-pirâmide. A de baixo, sem pontas e com duas bases, é de onde vem o sólido chamado tronco de pirâmide.
Viu como um corte muda tudo? Não é à toa que esse sólido tem fórmulas próprias de volume e área.
Quais são os elementos do tronco de pirâmide?
Antes de falarmos das fórmulas, vamos só dar uma olhada em conceitos que podem aparecer nas questões sobre tronco de pirâmide.
Resumindo as características mais importantes temos:
- Base maior (B): é a base original que restou da pirâmide de origem, costuma ser a face inferior. Pode ter vários formatos.
- Base menor (b): é a face formada pela secção transversal, que costuma ficar em cima. Apesar de ser menor, tem o mesmo formato da base maior.
- Faces laterais: serão sempre no formato trapezoidal.
- Arestas: são os segmentos de reta onde as faces se encontram.
- Vértices: são as quinas onde as arestas se encontram.
- Altura (h): é o segmento de reta vertical que liga a base menor à base maior, sempre formando um ângulo reto (90°).
- Apótema (a): é a “altura” de uma das faces laterais.
Atenção: uma questão pode dar, em uma mesma imagem, as medidas da pirâmide original que foi cortada junto com as medidas do tronco e da mini-pirâmide formada.
Cuidado para não confundir as medidas!
Normalmente, haverá traços e letras diferenciando-as. A altura da pirâmide, por exemplo, costuma vir indicada por H, a do tronco por h e a da mini-pirâmide por h’.
Resumindo, podemos dizer que H = h + h`.
É muita coisa para aprender, né? Por isso é que o Beduka faz um Plano de Estudos a cada ano. Assim você consegue ir se organizando para ver todas as matérias sem surtar!
Como calcular a área de um tronco de pirâmide?
É simples: a área do tronco da pirâmide será dada pela soma das áreas das faces!
Então precisamos calcular a área de cada polígono (lados e bases) e somá-las para dar a área total do tronco de pirâmide. Se falarmos em área lateral, é só excluir as bases da operação.
A conta dá menos trabalho do que você imagina:
- As bases têm o mesmo formato, então, você só precisa lembrar de uma fórmula e calcular para cada tamanho de base.
- Já as faces laterais são sempre trapezoidais, logo, é só usar a fórmula da área do trapézio uma vez e multiplicar o resultado pelo número de lados daquele tronco.
- Por fim é só somar os três valores.
Traduzindo tudo isso para uma expressão, teremos:
At = AB + Ab + Al
Sendo que:
At = área total do tronco.
AB = área da base maior.
Ab = área da base menor.
Al = área lateral da pirâmide.
Qual o volume de um tronco de pirâmide?
O jeito mais prático de calcular o volume do tronco da pirâmide é calcular o volume da pirâmide original e subtrair o volume da mini-pirâmide formada acima do corte transversal.
O restante corresponde justamente ao volume do tronco. É com base nesse raciocínio que chegamos à expressão da fórmula:
Vt = VP – Vp
Sendo que:
Vt = volume do tronco
VP = volume da pirâmide original
Vp = volume da pirâmide menor
Também é importante se aprofundar e entender como achar a apótema de um tronco de pirâmide e as propriedades de um tronco regular. Tem até uma outra fórmula para achar o valor diretamente, sem depender da pirâmide…
Por isso, fizemos um resumo completo sobre o tronco de pirâmide. Nele você encontra todos esses detalhes importantes!
Você achou que a explicação foi fácil de entender? Eu espero que tenha te ajudado, pois agora você já sabe tudo o que é essencial para acertar as questões de tronco de pirâmide.
Exercícios de tronco de pirâmide
Chegou a hora de testar seus conhecimentos com as questões abaixo:
1° dos exercícios de tronco de pirâmide – (Enem 2009)
Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19 cm de altura e 6 cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior —, espaçados de 1 cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.
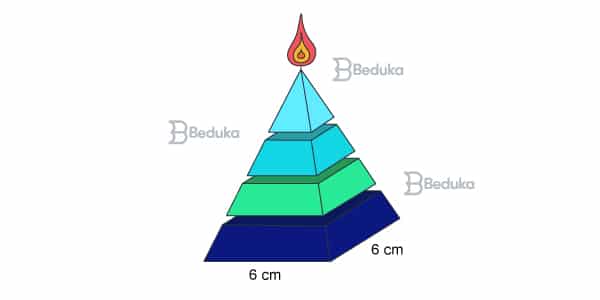
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
a) 156 cm³.
b) 189 cm³.
c) 192 cm³.
d) 216 cm³.
e) 540 cm³.
2° dos exercícios sobre tronco de pirâmide – (Enem 2020)
Uma das Sete Maravilhas do Mundo Moderno é o Templo de Kukulkán, localizado na cidade de Chichén Itzá, no México. Geometricamente, esse templo pode ser representado por um tronco reto de pirâmide de base quadrada.
As quantidades de cada tipo de figura plana que formam esse tronco de pirâmide são:
a) 2 quadrados e 4 retângulos.
b) 1 retângulo e 4 triângulos isósceles.
c) 2 quadrados e 4 trapézios isósceles.
d) 1 quadrado, 3 retângulos e 2 trapézios retângulos.
e) 2 retângulos, 2 quadrados e 2 trapézios retângulos.
3° das questões de tronco de pirâmide – (Enem)
Em São Paulo, no Parque do Ibirapuera, há um monumento de concreto chamado de Obelisco aos Heróis de 1032, uma homenagem aos que morreram na Revolução Constitucionalista de 1932. Esse monumento tem a forma de um tronco de pirâmide de base quadrada e tem 72m de altura. Suas bases possuem arestas de 9m e 7m.
Determine o custo de concreto utilizado na construção do Obelisco sabendo que o preço do metro cúbico de concreto utilizado na obra é de R$ 250,00.
a) R$ 800.000,00.
b) R$ 1.000.000,00.
c) R$ 1.158.000,00.
d) R$ 1.500.000,00.
e) R$ 2.200.000,00.
4° das questões sobre tronco de pirâmide – (FATEC)
Uma pirâmide regular, de 8 cm de altura, tem por base um quadrado cujos lados medem 12 cm. Ela é seccionada por um plano paralelo à base, que intercepta a altura no seu ponto médio. A área total do tronco de pirâmide obtido é, em centímetros quadrados, igual a:
a) 180.
b) 240.
c) 300.
d) 324.
e) 360.
5° dos exercícios de tronco de pirâmide – (UFRGS)
Considere a planificação do sólido formado por 2 faces quadradas e por 4 trapézios congruentes, conforme medidas indicadas na figura representada abaixo.
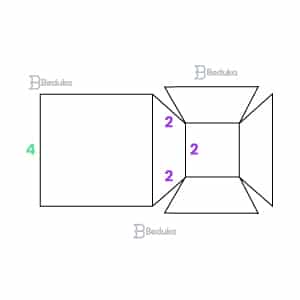
O volume desse sólido é:
a) 16(√2/3).
b) 28(√2/3).
c) 8√2.
d) 16√2.
e) 20√2.
- Ufa… Estamos quase na metade das atividades sobre tronco de pirâmide. Continue assim!
6° dos exercícios sobre tronco de pirâmide – (Mackenzie – SP)
Qual o volume de um tronco de pirâmide quadrangular regular, se os lados das bases medem 10 cm e 4 cm e a altura mede 4 cm?
a) 205 cm³.
b) 206 cm³.
c) 207 cm³.
d) 208 cm³.
e) 209 cm³.
7° das questões de tronco de pirâmide – (PUC)
Um tronco de pirâmide de bases quadradas tem 21 dm³ de volume. A altura do tronco mede 30 cm e o lado do quadrado de base maior, 40 cm. Então, o lado do quadrado de base menor mede:
a) 6 cm.
b) 8 cm.
c) 10 cm.
d) 12 cm.
e) 14 cm.
8° das questões sobre tronco de pirâmide – (EsPCEx 2009)
Um reservatório em forma de tronco de pirâmide regular de base quadrada e dimensões indicadas na figura deverá ter suas paredes laterais externas cobertas por uma tinta impermeável, cujo rendimento é de 11m² por galão.
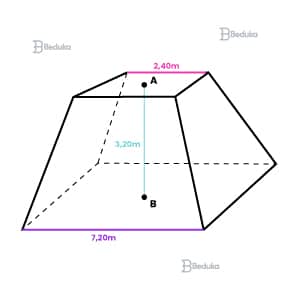
O número mínimo de galões que devem ser adquiridos para tal operação é:
a) 6.
b) 7.
c) 9.
d) 10.
e) 11.
9° dos exercícios de tronco de pirâmide – (PUC)
Corta-se uma pirâmide de 12 cm de altura por um plano paralelo à base, distando 4 cm desta. A razão entre a área da base e a área da seção é igual a:
a) 12/7 cm.
b) 7/4 cm.
c) 9/4 cm.
d) 7/9 cm.
e) 9/7cm.
10° das questões de tronco de pirâmide – (Escola Naval 2011)
As bases de um tronco de pirâmide triangular regular têm de perímetro, respectivamente, 54√3 m e 90√3 m . Se θ é o ângulo formado pela base maior com cada uma das faces laterais e a altura do tronco medindo 6√3m , então tg²θ vale
a) ⅓.
b) √3/3.
c) 1.
d) √3.
e) 3.
- Parabéns! Você acabou de resolver todas as atividades de tronco de pirâmide. Já tem noção de quantas acertou? Confira no próximo tópico!
Gabarito das questões de tronco de pirâmide
Agora que você já resolveu os exercícios, pode conferir seu desempenho com as respostas abaixo:
Resposta da questão 1
Alternativa correta: b) 189 cm³.
Resposta da questão 2
Alternativa correta: c) 2 quadrados e 4 trapézios isósceles.
Resposta da questão 3
Alternativa correta: c) R$ 1.158.000,00.
Resposta da questão 4
Alternativa correta: e) 360.
Resposta da questão 5
Alternativa correta: b) 28(√2/3).
Resposta da questão 6
Alternativa correta: d) 208 cm³.
Resposta da questão 7
Alternativa correta: c) 10 cm.
Resposta da questão 8
Alternativa correta: b) 7.
Resposta da questão 9
Alternativa correta: c) 9/4 cm.
Resposta da questão 10
Alternativa correta: e) 3.
Se você gostou do assunto e quer ficar por dentro das novidades do Beduka, você pode nos seguir no Instagram. Por lá, te atualizamos diariamente sobre as novidades do mundo do estudante.
Faça bom proveito de todo esse conteúdo!





