Para aprender sobre algumas grandezas físicas é necessário estudar a teoria, aprender como interpretar as fórmulas e fazer exercícios. Por isso, montamos esse super resumo para você aprender e testar seus conhecimentos com os melhores exercícios sobre Momento Angular! Não deixe de conferir as respostas no gabarito!
Se quiser ir diretamente para alguma parte do texto, clique em algum dos tópicos abaixo:
- O que é quantidade de movimento?
- O que é Momento Angular?
- Como calcular o Momento Angular?
- Quando ocorre conservação do Momento Angular?
- Exercícios sobre Momento Angular
- Gabarito dos Exercícios sobre Momento Angular
Problemas para descobrir a profissão ideal para você? Conheça o Raio-X do Beduka! Ele é um teste vocacional que te ajuda a nortear a escolha da sua carreira!
O que é Quantidade de Movimento?
Antes mesmo de aprender o que é o Momento Angular, você precisa entender o conceito de Quantidade de Movimento (Q).
Quantidade de Movimento é uma grandeza vetorial que é resultado da multiplicação da massa do corpo (kg – quilogramas) pela sua velocidade escalar (m/s – metros por segundo). Essa grandeza por ser expressa pela seguinte fórmula:
Q = m . v
A Quantidade de Movimento é importante pois através dela compreendemos o princípio da Conservação da Quantidade de Movimento. Neste princípio, considera-se que, na ausência de forças dissipativas, a Quantidade de Movimento inicial de um ou mais corpos, deve ser igual à Quantidade de Movimento final.
- São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
O que é Momento Angular?
O Momento Angular (L) é a forma de expressar a Quantidade de Movimento (Q) de um corpo quando este estiver em um movimento de rotação.
Esta é uma grandeza vetorial, possuindo módulo, direção e sentido.
Além disso, ela se relaciona com o deslocamento angular do corpo e com a sua velocidade escalar.
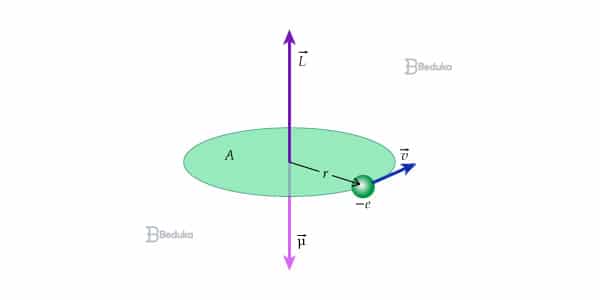
É a partir do ângulo formado entre a velocidade escalar do objeto e o eixo de rotação do movimento que será possível calcular o módulo do momento angular daquele corpo.

esquema momento angular
- Para dicas de estudo e resumos ilustrados, acesse o Pinterest do Beduka!
Como calcular o Momento Angular?
O primeiro passo para calcular o momento angular de um objeto é analisar o ângulo formado pela Quantidade de Movimento e o raio do eixo de rotação. Este é o primeiro passo pois caso o ângulo formado seja perpendicular ao eixo, formando 90º graus, a conta será simplificada.
Fórmula para cálculo do Momento Angular:
L = r . Q . senθ
L = Momento Angular
r = Raio de rotação
Q = Quantidade de Movimento → Q = m . v
senθ = seno do ângulo formado entre o r e Q
Caso o Ângulo formado seja de 90°, podemos substituir a fórmula acima por:
L = r . m . v
Isso acontece porque o seno do ângulo de 90° é igual a 1.
Além disso, outra substituição pode ser feita. Considerando que a velocidade escalar (v) é igual a multiplicação da velocidade angular com o raio de rotação, temos:
L = r . m (𝛚 . r)
L = m𝛚r2
- Decorar as fórmulas pode ser difícil, mas é extremamente útil em questões que você precise fazer substituições para chegar ao resultado final. Fique atento!
Quando ocorre conservação do Momento Angular?
Seguindo o mesmo princípio da conservação da Quantidade de Movimento, a Conservação do Momento Angular só irá ocorrer na ausência de forças dissipativas.
Isto é, quando toda a energia do sistema é mantida pois não existe uma resultante de forças externas sobre o próprio sistema.
Em especial na conservação do Momento Angular, como estamos tratando de um movimento em que existe um processo de rotação, é importante que não exista torque nesse sistema. Mas afinal, o que seria torque?
O torque é um vetor de força que está perpendicular ao plano formado pela força e raio de rotação do movimento. Caso ocorra sobre o corpo em um movimento de rotação, este poderá ganhar velocidade angular, atrapalhando assim a conservação do Momento Angular.
Deste modo, a conservação do Momento Angular depende da relação entre a velocidade angular e o momento de inércia. Esta grandeza mede como o formato do corpo pode influenciar no movimento de rotação do próprio corpo.
Pense na seguinte situação:
Uma bailarina girando em torno do seu próprio eixo. Ao abrir os braços ela diminui a sua velocidade de rotação e quando ela fecha os braços, aproximando-os do seu corpo (eixo de rotação) ela ganha velocidade.
Essa alteração da posição dos braços altera o momento de inércia e, dessa maneira, altera também a velocidade angular. Como o Momento Angular também pode ser expresso pela relação da velocidade angular (𝛚) com o momento de inércia ( i ), temos que:
L = 𝛚 . i
Ou seja, para que ocorra a conservação do Momento Angular irá existir um balanço entre esses fatores:
L inicial = L final só ocorre quando (𝛚 . i) inicial = (𝛚 . i) final.
Exercícios sobre Momento Angular
- Esperamos que o resumo tenha te ajudado! Teste agora seus conhecimentos e confira as respostas no Gabarito. Lembre-se: o Beduka está aqui para te ajudar a alcançar o sonho da vaga no Ensino Superior!
Questão 1- (FUVEST) Um corpo de massa 3 kg move-se a uma velocidade escalar constante de 4 m/s sobre um círculo de raio 5 m. Após algumas revoluções sobre o círculo, o corpo escapa e se movimenta em linha reta, mantendo o mesmo valor de velocidade e a mesma direção do instante de escape. O momento angular do corpo antes de escapar e o momento angular do corpo após o escape, calculados em relação ao centro do círculo são (em kg m2 /s), respectivamente, de:
a) 12 e 0
b) 12 e 12
c) 60 e 60
d) 60 e 12
e) 60 e 0
Questão 2- (FUVEST) Uma pessoa de massa m está parada na borda de uma plataforma horizontal, de forma circular, com raio R e momento de inércia I, que pode girar livremente em torno de um eixo vertical que passa pelo centro desse círculo. Inicialmente, a plataforma está em repouso em relação ao solo. Num dado instante, a pessoa começa a andar ao longo da borda da plataforma, até atingir uma velocidade de módulo v em relação ao solo. Nesse instante, a velocidade angular da plataforma vale:
a) zero
b) v/R
c) mvR/I
d) Iv/mR3
e) v /m/I
Questão 3- (FUVEST) Uma criança senta-se num banco giratório com os braços encostados ao corpo e pede que façam girar o banco em torno de um eixo vertical que passa pelo centro do sistema criança banco. Num dado instante, com o sistema criança banco a girar solidariamente, a criança abre os braços e volta a encostá-los ao corpo. Considere desprezível o efeito do atrito entre o banco e o eixo vertical. Selecione a afirmação verdadeira.
a) Quando a criança abre os braços, o momento de inércia do sistema, em relação ao eixo de rotação, diminui.
b) Quando a criança abre os braços, o módulo da velocidade angular do sistema diminui.
c) Quando a criança fecha os braços, o momento de inércia do banco, em relação ao seu centro de massa, diminui.
d) Quer a criança abra ou feche os braços, o módulo da velocidade angular do sistema mantém-se.
e) Quer a criança abra ou feche os braços, o momento angular do banco, em relação ao eixo de rotação, mantém-se.
Questão 4- (FUVEST) Durante o movimento, o valor máximo do módulo do momento angular do corpo em relação à origem do sistema de coordenadas é:
a) mωR2
b) mωR(d R)
c) mωR(d R)
d) mω(d R)2
e) mωRd
Questão 5- (FUVEST) Uma plataforma circular, de massa M e raio R, gira livremente, com velocidade angular ω, em torno de um eixo fixo, perpendicular a ela, passando pelo seu centro. Seu momento de inércia em relação a esse eixo é I MR2 2 . Uma pequena bola de material viscoso, de massa m, cai verticalmente sobre a plataforma, à distância R 2 do seu centro, grudando-se nela instantaneamente. A velocidade angular final da plataforma é:
a) M – m / M (ω)
b) M + m / M (ω)
c) M / M + m (ω)
d) 2M – m / 2M (ω)
e) 2M / 2M + m (ω)
- Parabéns, você fez todos os exercícios sobre Movimento Angular. Confira agora o Gabarito:
Gabarito dos Exercícios sobre Momento Angular
Exercício resolvido da questão 1 –
Alternativa correta: c) 60 e 60
Exercício resolvido da questão 2 –
Alternativa correta: c) mvR/I
Exercício resolvido da questão 3 –
Alternativa correta: b) Quando a criança abre os braços, o módulo da velocidade angular do sistema diminui.
Exercício resolvido da questão 4 –
Alternativa correta: c) mωR(d R)
Exercício resolvido da questão 5 –
Alternativa correta: e) 2M / 2M + m (ω)
- Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos exercícios sobre Movimento Angular? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.