As funções são apenas expressões matemáticas nas quais se mudarmos o valor, o resultado também muda. No caso da função do 1º Grau, há uma estrutura que está sempre presente: f(x)=ax+b, Parece complicado? Vem ler o resumo e depois treinar com os exercícios de Função do Primeiro Grau!
Neste artigo, você encontrará todos os temas abaixo. Clique em um dos tópicos para ir direto ao conteúdo da sua escolha:
- O que é uma função?
- Como é a Função de Primeiro Grau?
- Gráfico da Função do Primeiro Grau?
- Lista de exercícios de Função do Primeiro Grau.
- Gabarito dos exercícios sobre Função do Primeiro Grau.
Quando você terminar as questões de Função do Primeiro Grau, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil.
O que é uma função?
Uma função é como se fosse um tipo especial de equação. Nela, nós temos uma expressão com um valor que pode mudar. A medida que ele muda, o resultado também muda.
O valor que pode mudar é chamado de incógnita, representado pela letra x. Já a letra y ou f(x) é o resultado que muda em função de x.
Para cada valor de x, pode-se estabelecer um valor de y, por isso dizemos que “y está em função de x”. Por essa razão, x e y são conhecidos, respectivamente, como variável independente e variável dependente.
Então, função é uma regra matemática que relaciona cada elemento x de um conjunto (domínio) a um único elemento y que está em outro conjunto (contradomínio). Essa relação entre os elementos se dá pela lei de formação, que é a lei que define uma função.
E a função do Primeiro Grau?
A função do primeiro grau é uma leique relaciona cada elemento de um conjunto a um único elemento de outro, e ondea variável independente, no caso o x, é uma potência de expoente 1.
O grau de uma função é dado pelo maior expoente da variável independente. No caso das funções do primeiro grau, o maior expoente é 1.Uma função do primeiro grau é aquela em que a lei de formação pode ser escrita na seguinte maneira:
f(x) = ax + b
Onde a e b pertencem ao conjunto dos números reais, e a é diferente de zero. Esta função pode ser chamada de função afim, e também pode ser descrita como y = ax = b.
Exemplos:
- f(x) = 6x – 2, onde a = 6 e b = -2;
- f(x) = -5x + 4, onde a = -5 e b = 4;
- f(x) = 8x, onde a = 8 e b = 0.
Gráfico de uma Função do Primeiro Grau
A função de 1º grau pode ser representada por uma reta em um gráfico no plano cartesiano.
Para representá-lo, é necessário encontrar dois pares ordenados de pontos pertencentes a essa reta. Depois, colocá-los no plano cartesiano e traçar a reta que passa por eles.
Veja o exemplo de uma função do primeiro grau e o gráfico referente: y = 3x – 1.
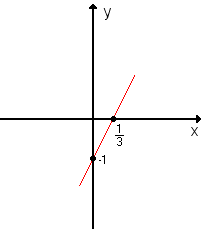
- x = 0, temos y = 3 · 0 – 1 = -1; dessa maneira, um ponto é (0, -1).
- y = 0, temos 0 = 3x – 1; dessa maneira, e outro ponto é.
Simples né? Há mais de 200 resumos como esse no Instagram do Beduka!
Exercícios de Função do Primeiro Grau
Questão 1 – (UFPI)
A função real de variável real, definida por f (x) = (3 – 2a).x + 2, é crescente quando:
a) a > 0.
b) a < 3/2.
c) a = 3/2.
d) a > 3/2.
e) a < 3.
Questão 2 – (FGV)
O gráfico da função f (x) = mx + n passa pelos pontos (– 1, 3) e (2, 7). O valor de m é:
a) 5/3.
b) 4/3.
c) 1.
d) 3/4.
e) 3/5.
Questão 3 – (UNIFOR)
A função f, do 1° grau, é definida por f(x) = 3x + k. O valor de k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é:
a) 2.
b) 1.
c) 3.
d) 4.
e) 5.
- Muito bem! Você está na metade das questões sobre Função do Primeiro Grau!
Questão 4- (ACAFE)
Um táxi começa uma corrida com o taxímetro marcando R$ 4,00. Cada quilômetro rodado custa R$1,50. Se ao final de uma corrida, o passageiro pagou R$ 37,00 , a quantidade de quilômetros percorridos foi:
b) 11.
c) 33.
e) 32.
d) 22.
a) 26.
Questão 5 – (EDSON QUEIROZ – CE)
O gráfico abaixo representa a função de ? em ? dada por f(x) = ax + b (a, b Î?). De acordo com o gráfico conclui-se que:
a) a < 0 e b >0.
b) a < 0 e b < 0.
c) a > 0 e b > 0.
d) a > 0 e b < 0.
e) a > o e b = 0.
- Ufa, estamos quase lá! Faça os dois últimos exercícios sobre Função do Primeiro Grau!
Questão 6 – (ENEM 2016)
Para uma feira de ciências, dois projéteis de foguetes, A e B, estão sendo construídos para serem lançados. O planejamento é que eles sejam lançados juntos, com o objetivo de o projétil B interceptar o A quando esse alcançar sua altura máxima. Para que isso aconteça, um dos projéteis descreverá uma trajetória parabólica, enquanto o outro irá descrever uma trajetória supostamente retilínea. O gráfico mostra as alturas alcançadas por esses projéteis em função do tempo, nas simulações realizadas.
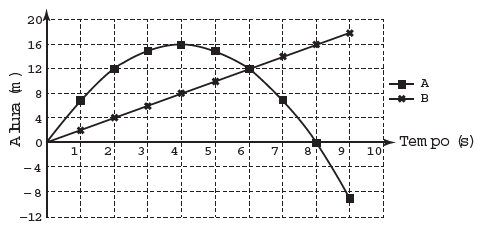
Com base nessas simulações, observou-se que a trajetória do projétil B deveria ser alterada para que o objetivo fosse alcançado.
Para alcançar o objetivo, o coeficiente angular da reta que representa a trajetória de B deverá
a) diminuir em 2 unidades.
b) diminuir em 4 unidades.
c) aumentar em 2 unidades.
d) aumentar em 4 unidades.
e) aumentar em 8 unidades.
Questão 7 – (ENEM 2016)
Uma cisterna de 6 000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada junto com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.
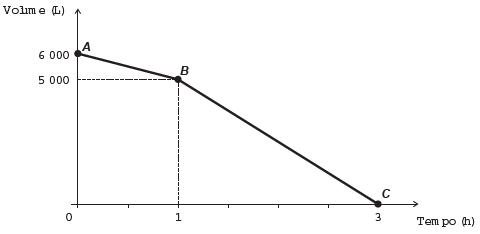
Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?
a) 1 000.
b) 1 250.
c) 1 500.
d) 2 000.
e) 2 500.
- Parabéns, você fez todas as questões de Função do Primeiro Grau!
Respostas dos Exercícios sobre Função do Primeiro Grau
Exercício resolvido da questão 1
Alternativa correta: b) a < 3/2.
Exercício resolvido da questão 2
Alternativa correta: b) 4/3.
Exercício resolvido da questão 3
Alternativa correta: e) 5.
Exercício resolvido da questão 4
Alternativa correta: d) 22.
Exercício resolvido da questão 5
Alternativa correta: a) a < 0 e b >0.
Exercício resolvido da questão 6
Alternativa correta: c) aumentar em 2 unidades.
Exercício resolvido da questão 7
Alternativa correta: c) 1 500.
Gostou dos nossos exercícios de Função do Primeiro Grau?Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, mensalidade e muito mais.
Experimente agora!





