Hipérboles advém de um corte que é feito no cone (seção cônica) onde formam-se duas “meia luas” opostas. Hipérbole é conjunto de todos os pontos coplanares para os quais a diferença das distâncias a dois pontos fixos (focos) é constante. Leia nosso resumo e faça nossa lista de exercícios sobre Hipérbole dos melhores vestibulares do país.
Quando você terminar as questões sobre Hipérbole, faça nosso Simulado Enem. Coloque em prática todo o seu estudo, escolhendo as matérias que deseja treinar.
As Hipérboles são estudadas por um campo da matemática denominado de Geometria Analítica
A Geometria Analítica estuda o objeto matemático, figura geométrica, forma, entre outros, que possam ser representados no espaço geometricamente por um desenho ou algebricamente por uma fórmula. A geometria analítica une a geometria com a álgebra, permitindo a criação de fórmulas matemáticas.
Neste post aprenderemos a resolver questões envolvendo Hipérbole, que são figuras geométricas específicas, e ao final você colocará seu conhecimento em prática com exercícios sobre Hipérbole.
- Aproveita também a lista de exercícios sobre Geometria Analítica que fizemos para você!
O que é Hipérbole?
Considere F¹ e F2² como sendo dois pontos diferentes do plano e 2c a distância existente entre eles. A Hipérbole é o conjunto dos pontos do plano, onde a diferença, em valor absoluto, das distâncias à F¹ e F² é a constante 2a (0 <2a <2c).
Para conseguir entender o parágrafo anterior e os próximos tópicos, veja a figura abaixo:
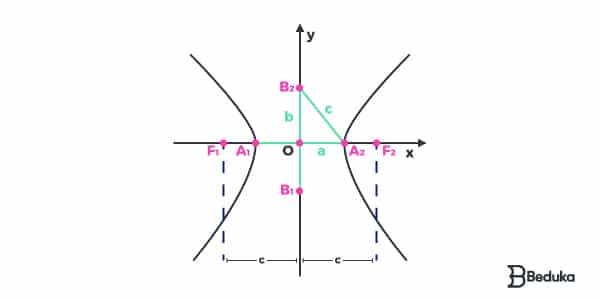
Quais são os elementos da Hipérbole?
- Focos: são os pontos F¹ e F²;
- Distância focal: distância entre os dois focos denominada de 2c;
- Centro: ponto médio do segmento criado pela distância entre os dois focos;
- Eixo real: A hipérbole intercepta o segmento F¹F² nos pontos A¹ e A². o segmento gerado pela distância entre A¹ e A² é denominado de eixo real, que possui comprimento igual a 2a
- Eixo imaginário: é o segmento de reta B¹B² perpendicular ao eixo real, com ponto médio no centro da hipérbole. O comprimento do eixo imaginário é igual a 2b;
- Excentricidade: é a razão a seguir.
Quais são as equações reduzidas da hipérbole
1° caso – Onde a hipérbole possui os focos sobre o eixo x e centro sobre a origem de um plano cartesiano:
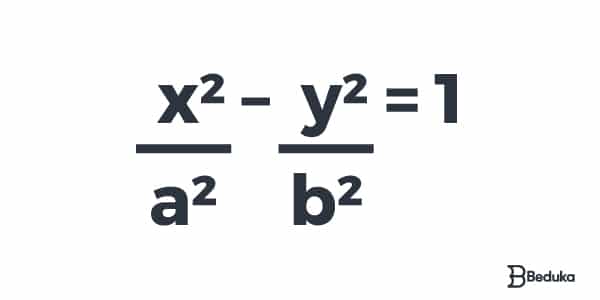
2° caso – Onde a hipérbole também possui centro na origem, mas seus focos estão sobre o eixo y do plano cartesiano:
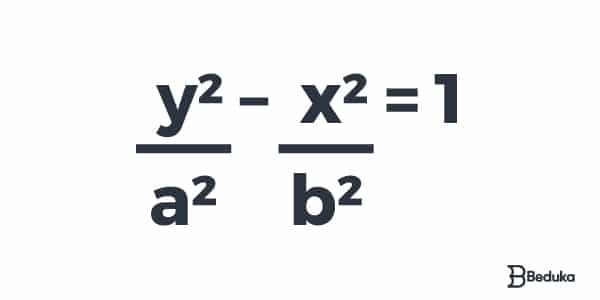
Exercícios sobre Hipérbole com Gabarito
Que tal testar seu conhecimento com exercícios sobre Hipérbole? Assim você pode se certificar que entendeu esse conteúdo tão valioso para o ENEM.
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Aliás, Parabéns por ter lido até aqui. Você teve uma sábia decisão e está pronto para fazer as questões dos melhores vestibulares do país que separamos para você!
Questão 1 – (UFAM) Os pontos A(4, 0) e B(0, 6) são extremos de um diâmetro da circunferência. Então, a equação reduzida da circunferência é:
a) x2 + y2 – 6x – 4y = 0
b) x2 + y2 – 4x – 6y = 0
c) x2 + y2 + 4x – 6y = 0
d) x2 + y2 + 4x + 6y = 0
e) x2 + y2 – 6x + 4y = 0
Questão 2 – (PUC-Rio) O número de pontos de intersecção das duas parábolas y = x2 e y = 2x2 – 1 é:
a) 0
b) 1
c) 2
d) 3
e) 4
Questão 3 – (IFPB) Dados dois pares ordenados (2,-4) e (2,0) que representam os vértices de um hipérbole de foco (2, -2 + √13), calcule a equação da hipérbole que satisfaça as condições dadas.
a) 4x² – 9y² – 16x – 36y +16 = 0
b) 2x² – 3y² – 16x – 36y + 16 = 0
c) 4x² – 9y² + 16x – 36y – 16 = 0
d) 4x² − 5y² − 16x – 36y + 16 = 0
e) 4x² – 16x – 36y + 16 = 0
Questão 4 – (FUMARC 2013) Um artista recebeu uma encomenda para fazer um painel, esculpindo em uma chapa de aço folhas e flores. Para determinar o formato do painel, o artista considerou a chapa de aço como um plano cartesiano cujos eixos a dividiram em quatro quadrantes. Utilizou um segmento de reta e o deslocou nesse plano cartesiano, de tal forma que uma das extremidades permanecia sempre no eixo y e o seu ponto médio permanecia sempre no eixo x. Dessa maneira, o formato da figura desenhada pela outra extremidade é uma
a) elipse.
b) parábola.
c) hipérbole.
d) circunferência.
Questão 5 – (Petrobrás – Cesgranrio 2010) Os vértices imaginários da hipérbole de equação abaixo são:
a) (2,1) e (2,3)
b) (2,0) e (2,2)
c) (2,0) e (1,2)
d) (1,1) e (1,2)
e) (1,0) e (1,2)
Questão 6 – (IDECAN) Dados dois pares ordenados (2,-4) e (2,0) que representam os vértices de um hipérbole de foco (2, -2 + √13), calcule a equação da hipérbole que satisfaça as condições dadas.
a) 4x2 – 9y2 – 16x – 36y +16 = 0
b) 2x2 – 3y2 – 16x – 36y + 16 = 0
c) 4x2 – 9y2 + 16x – 36y – 16 = 0
d) 4x2 − 5y2 − 16x – 36y + 16 = 0
e) 4x2 – 16x – 36y + 16 = 0
Gabarito dos Exercícios sobre Hipérbole
Exercício resolvido da questão 1 –
Alternativa correta: b) x2 + y2 – 4x – 6y = 0
Exercício resolvido da questão 2 –
Alternativa correta: c) 2
Exercício resolvido da questão 3 –
Alternativa correta: a) 4x² – 9y² – 16x – 36y +16 = 0
Exercício resolvido da questão 4 –
Alternativa correta: a) elipse.
Exercício resolvido da questão 5 –
Alternativa correta: e) (1,0) e (1,2)
Exercício resolvido da questão 6 –
Alternativa correta: a) 4x2 – 9y2 – 16x – 36y +16 = 0
Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos Exercícios sobre Hipérbole? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.





