A geometria analítica é um ramo da Matemática que estuda o objeto matemático, figura geométrica, forma, entre outros, que possam ser representados no espaço geometricamente por um desenho ou algebricamente por uma fórmula. A geometria analítica une a geometria com a álgebra, permitindo a criação de fórmulas matemáticas.
O matemático e filósofo francês René Descartes (1596-1650), foi o criador do pensamento cartesiano, da geometria analítica, conhecida também como geometria cartesiana. Ele desenvolveu vários trabalhos na área da filosofia, ciências e matemática. Relacionou a álgebra com a geometria, havendo assim a criação da geometria analítica e o sistema de coordenadas, denominada atualmente como Plano Cartesiano.
Os objetos, figuras e relações da geometria plana são focos de estudos da geometria analítica. Essa maneira de estudar os elementos geométricos é outra forma de analisar conceitos que já existiam e completar com novos conhecimentos. Um dos principais conceitos é a distância entre um ponto e uma reta.
A representação dos pontos de uma reta utilizando os números reais é a base principal da geometria cartesiana. O ponto representa um único número real. Este é alcançado pela distância entre o ponto e o início da reta.
A distância é primordial nessa matéria. Com ela, é possível desenvolver outros assuntos e, assim, novos conceitos surgem, como o círculo e a circunferência.
- Veja a representação do ponto, da reta e do número real na figura abaixo:
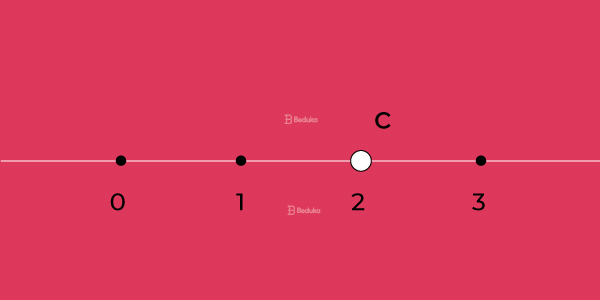
Depois de um tempo, o ponto passou a ser representado no plano. Este é representado por um par de números reais, chamado também de par ordenado.
- Veja a representação do par ordenado na figura abaixo:
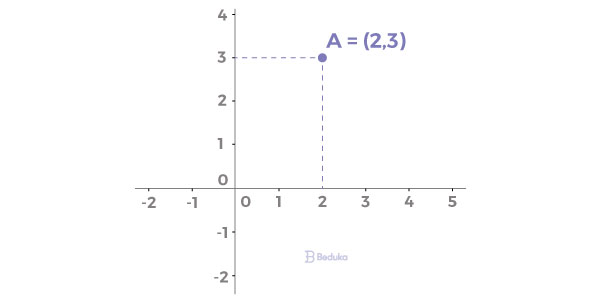
Existem também os ternos ordenados, que são representados por pontos no espaço por um conjunto de três números reais.
Para fazer os exercícios de geometria analítica, é importante saber que uma coordenada do ponto é o número real. A reta é o espaço onde o espaço está localizado, sendo chamado de dimensão.
O número de coordenadas que um ponto possui é proporcional ao número de dimensões do espaço onde está localizado. Para ficar mais fácil, vamos imaginar um ponto que possui três dimensões. Logo, ele também terá três coordenadas.
É preciso definir o tempo de estudo de cada matéria e a prioridade de cada uma. Não é difícil e fica mais fácil com o nosso plano de estudos gratuito.
Exercícios de Geometria Analítica
1 – (Fuvest-SP) – Se (m+2n , m – 4) e (2 – m , 2n) representam o mesmo ponto do plano cartesiano, então mn é igual a:
a) – 2
b) 0
c) √2
d) 1
e) ½
2 – (FEI-SP) – Num sistema de coordenadas cartesianas são dados os pontos A(0 , 0) e P(3 , h). Assinale a alternativa cuja expressão representa a distância do ponto P ao ponto A em função de h.
a) d=√(9+h2 )
b) d=h+3
c) d=3h
d) d= √(9+6h+h2 )
e) d=9+h
3 – (Fatec – SP) – Assinale a alternativa verdadeira.
a) Três retas que, duas a duas, não têm ponto em comum são paralelas.
b) Dadas duas retas paralelas distintas, por uma delas passa um, e somente um, plano paralelo à outra reta.
c) por um ponto de uma reta pode-se traçar uma, e somente uma, perpendicular à reta considerada.
d) Por um ponto não pertencente a um plano pode-se traçar mais de uma reta paralela ao plano considerado.
e) Três pontos determinam um único plano.
4 – (Unirio) – A função linear f(x) = ax + b é representada por uma reta que contém o ponto (2,-1) e que passa pelo vértice da parábola y = 4x – 2x². A função é:
a) f(x) = -3x + 5
b) f(x) = 3x – 7
c) f(x) = 2x – 5
d) f(x) = x – 3
e) f(x) = x/3 – 7/3
5 – (PUC-SP) – Os pontos A=(-1; 1), B=(2; -1) e C=(0; -4) são vértices consecutivos de um quadrado ABCD. A equação da reta suporte da diagonal BD, desse quadrado, é:
a) x + 5y + 3 = 0.
b) x – 2y – 4 = 0.
c) x – 5y – 7 = 0.
d) x + 2y – 3 = 0.
e) x – 3y – 5 = 0.
6 – (CFO ES – Exatus 2013) – Sendo “S” denominada de área do polígono determinado pelas coordenadas cartesianas dos pontos A(5,0), B(2,3), C(1,0) e D(6,5), qual o valor de S?
a) 15
b) 12
c) 10
d) 28
e) 21
7 – (PM ES – Exatus 2013) – Clarence desenhou o triângulo determinado pelas coordenadas dos pontos cartesianos A(7;5), B(3;2) e C(7;2). Ao calcular a área e o perímetro desse triângulo, os valores obtidos foram, respectivamente:
a) 3 e 3
b) 3 e 6
c) 6 e 6
d) 6 e 12
e) 12 e 12
Agora que já respondeu todos os nossos exercícios de geometria analítica, chegou a hora de conferir as respostas com o nosso gabarito.
Respostas dos Exercícios de Geometria Analítica
Exercício resolvido da questão 1
e) ½
Exercício resolvido da questão 2
a) d=√(9+h2 )
Exercício resolvido da questão 3
d) Por um ponto não pertencente a um plano pode-se traçar mais de uma reta paralela ao plano considerado.
Exercício resolvido da questão 4
a) f(x) = -3x + 5
Exercício resolvido da questão 5
c) x – 5y – 7 = 0.
Exercício resolvido da questão 6
a) 15
Exercício resolvido da questão 7
d) 6 e 12
Você pode testar os seus conhecimentos sobre os temas mais cobrados no ENEM usando o Simulado Beduka. É totalmente online e gratuito. Você pode escolher quais matérias praticar, quantos exercícios, montar o seu próprio simulado, e muito mais. Treine quantas vezes quiser! Acesse o Simulado Beduka.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!