Essa matéria assusta muitos alunos, mas não deveria. Vamos te mostrar como a trigonometria no triângulo retângulo é algo muito tranquilo! As fórmulas dessa matéria são basicamente três: Seno, Cosseno e Tangente. Leia o resumo com a explicação, veja os exemplos e treine com os melhores exercícios de Trigonometria no triângulo retângulo. Tem gabarito!
Neste artigo, você encontrará todos os temas abaixo. Clique em um dos tópicos para ir direto ao conteúdo da sua escolha:
- O que é Trigonometria?
- Trigonometria no Triângulo retângulo: Seno, Cosseno e Tangente.
- O que são ângulos notáveis? Veja tabela e macete!
- Como usamos tudo isso em uma questão?
- Lista de exercícios de Trigonometria!
- Gabarito dos exercícios de Trigonometria.
Quando você terminar as questões de Trigonometria no triângulo retângulo, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil.
O que é Trigonometria?
Nós sabemos, muita gente tem birra da trigonometria. Mas não precisa ser assim, ela é mais legal do que aparenta! Além do mais, nós vamos trabalhar só com a parte básica.
A trigonometria é uma ferramenta matemática que leva em conta os ângulos e os lados que o formam.
Você lembra das relações de semelhança nos triângulos? A ideia que a trigonometria traz é parecida: sempre que pegarmos dois valores específicos e dividimos eles, nos dará um mesmo resultado.
Até aqui tudo bem? Então vamos para a parte prática:
Trigonometria no triângulo retângulo
Antes de tudo precisamos lembrar as características do triângulo retângulo:
- É preciso que um de seus ângulos seja 90° (reto).
- A soma de todos os três ângulos resulta em 180°.
- O lado maior é o lado oposto ao ângulo reto, chamado de hipotenusa.
- Os outros dois lados são chamados de cateto.
O que é Seno, Cosseno e Tangente?
A trigonometria diz que, no triângulo retângulo, podemos estabelecer três relações:
- Seno: é um valor específico encontrado para cada ângulo, quando pegamos o cateto (lado) oposto a ele e dividimos pela hipotenusa.
- Cosseno: é um valor específico encontrado para cada ângulo, quando pegamos o lado que encosta nele (adjacente) e dividimos pela hipotenusa.
- Tangente: é um valor específico encontrado para cada ângulo, quando pegamos o cateto oposto e dividimos pelo adjacente.
Viu? Tudo tranquilo. Podemos colocar essas informações em fórmulas:
- Sen x° = cat. oposto / hipotenusa
- Cos x° = cat. adjacente / hipotenusa
- Tg x° = cat. oposto / cat. adjacente
Simples né? Há mais de 200 resumos como esse no Instagram do Beduka!
Como memorizar as fórmulas trigonométricas?
Você tem dificuldade para decorar essas fórmulas e acaba se enrolando na hora da prova?
Temos algumas maneiras diferentes para te ajudar a se lembrar quando for resolver exercícios de trigonometria no triângulo retângulo.
- Andou de COStas? CA Hi (COSseno = Cateto Adjacente dividido pela Hipotenusa)
- Está SENo roubado? COrHI (SENo = Cateto Oposto dividido pela Hipotenusa)
- Tá Gostoso? CO CA (Tangente = Cateto Oposto dividido pelo Cateto Adjacente)
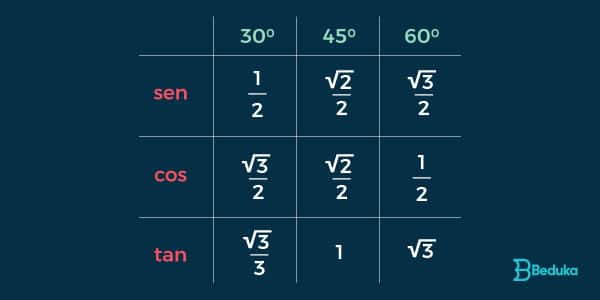
O que são Ângulos Notáveis?
Existem alguns ângulos que sempre aparecem nas questões, eles são chamados de ângulos notáveis.
São eles: 30°, 45° e 60°.
Além deles, temos o 0°, 90° e o 180°.
Normalmente, as escolas e os vestibulares esperam que nós tenhamos decorado o seno, cosseno e tangente de cada um deles. Quanto aos demais ângulos, sempre vem a tabela ou a informação.
É bom fazer manter um resumo como esse por perto:
Como faço para decorar a tabela?
Essa você vai ter que decorar, não tem outro jeito! Mas há uma forma fácil de memorizar essa tabela, siga a sequência assim:
Na horizontal, escreva os ângulos em ordem crescente.
Na vertical, de cima para baixo: Seno, Cosseno e Tangente.
Em seguida preencha assim:
- 1, 2, 3 na primeira linha
- 3, 2, 1 na segunda linha
- Todos sobre 2 e raiz onde não tem 1.
- Depois basta acrescentar em ordem: 3√3, 1 e √3
Tente cantar essa sequência e veja que há uma sonoridade: 1, 2, 3, 3, 2, 1; todos sobre 2 e raiz onde não tem 1.
Como usamos trigonometria em uma questão?
A primeira coisa é ler o enunciado e destacar as informações. Em cada exercício você verá os valores que tem e qual você precisa descobrir.
Depois, você faz o desenho para ver qual ângulo foi dado, onde e como ele está em relação aos lados que você sabe o valor.
Depois é só escolher a fórmula mais adequada:
- Se você tiver um ângulo e o valor de um lado oposto a ele, poderá achar a hipotenusa com a fórmula do seno ou o lado adjacente com a fórmula da tangente.
- Se você tiver um ângulo e o valor de um lado adjacente a ele, poderá achar a hipotenusa com a fórmula do cosseno ou o lado oposto com a fórmula da tangente.
- Se você não tiver o ângulo mas tiver o valor do lado oposto e do lado adjacente, pode descobrir qual é esse ângulo!
Então é só substituir as informações naquelas fórmulas e calcular. Pronto!
Exercícios de Trigonometria no triângulo retângulo
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Parabéns por ter lido até aqui!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1 – (Cesgranrio)
Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:
a) 6√3 m.
b) 12 m.
c) 13,6 m.
d) 9√3 m.
e) 18 m.
Questão 2 – (UFAM)
Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente, então a tangente do ângulo oposto ao menor lado é:
a) 2√3.
b) √3/3.
c) √3/6.
d) √20/20.
e) 3√3.
Questão 3 – (Beduka)
Uma aeronave decolou fazendo um ângulo de 20° em relação ao chão. A sombra desse avião no chão percorreu 500 m. A qual altura o avião se encontra neste momento?
Considere: sen 20º = 0,34 / cos 20º = 0,93 / tg 20º = 0,36
- Muito bem! Você está na metade das questões sobre Trigonometria no triângulo retângulo!
Questão 4 – (Enem)
Raios de luz solar estão atingindo a superfície de um lago formando um ângulo X com a sua superfície, conforme indica a figura.
Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por I(x) = k . sen(x)
sendo k uma constante, e supondo-se que X está entre 0° e 90º.
Quando x = 30º, a intensidade luminosa se reduz a qual percentual de seu valor máximo?
a) 33%.
b) 50%.
c) 57%.
d) 70%.
e) 86%.
Questão 5 – (Cefet – PR)
A rua Tenório Quadros e a avenida Teófilo Silva, ambas retilíneas, cruzam-se conforme um ângulo de 30º. O posto de gasolina Estrela do Sul encontra-se na avenida Teófilo Silva a 4000 m do citado cruzamento.
Sabendo que o percurso do posto Estrela do Sul até a rua Tenório Quadros forma um ângulo de 90° no ponto de encontro do posto com a rua Teófilo Silva, determine em quilômetros, a distância entre o posto de gasolina Estrela do Sul e a rua Tenório Quadros.
- Ufa, estamos quase lá! Faça os dois últimos exercícios sobre Trigonometria no triângulo retângulo!
Questão 6 – (UFPI – adaptada)
Um avião decola formando com o solo, um ângulo de 30º (suponha que a região sobrevoada pelo avião seja plana). Depois de percorrer 1 000 metros em trajetória retilínea, qual a altura atingida pelo avião?
Questão 7 – (Unisinos – RS)
Um avião levanta voo sob um ângulo constante de 20º. Após percorrer 2 000 metros em linha reta, qual será a altura atingida pelo avião, aproximadamente? (Utilize: sem 20º = 0,342; cos 20º = 0,94 e tg 20º = 0,364)
- Parabéns, você fez todas as questões de Trigonometria no triângulo retângulo!
Gabarito dos exercícios sobre Trigonometria no triângulo retângulo
Exercício resolvido da questão 1 –
Alternativa correta: e) 18 m.
Exercício resolvido da questão 2 –
Alternativa correta: b) √3/3.
Exercício resolvido da questão 3 –
Alternativa correta: 181,3 m.
Exercício resolvido da questão 4 –
Alternativa correta: b) 50%.
Exercício resolvido da questão 5 –
Alternativa correta: 2,3 km aproximadamente.
Exercício resolvido da questão 6 –
Alternativa correta: 500 m.
Exercício resolvido da questão 7 –
Alternativa correta: 684 m.
Gostou dos nossos exercícios de Trigonometria no triângulo retângulo?Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, mensalidade e muito mais.
Experimente agora!





