Matriz é o nome que damos a uma representação matemática das tabelas. Assim, uma matriz A (m x n) indica que ela possui “m” linhas e “n” colunas. Simples não é? Leia o artigo para saber mais e teste seus conhecimentos com os exercícios de Matrizes!
Neste artigo, você encontrará todos os temas abaixo. Clique em um dos tópicos para ir direto ao conteúdo da sua escolha:
- O que é Matriz?
- Quais são os tipos de matrizes?
- Como fazer operações com as matrizes?
- Lista de exercícios de Matrizes.
- Gabarito dos exercícios sobre Matrizes.
Quando você terminar as questões de Matriz, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil.
O que é Matriz?
As matrizes são formas matemáticas de armazenar informações. É como se traduzíssemos os dados de uma tabela.
Muitos alunos a temem, mas ela é apenas uma representação em que as próprias posições transmitem informações. Para saber ler suas “entrelinhas”, precisamos estudar seus elementos!
Elementos de uma matriz
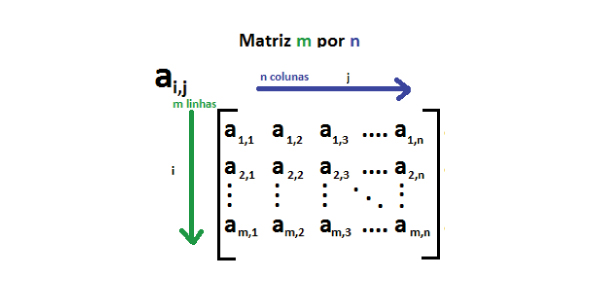
As matrizes são sempre representadas por letras maiúsculas (A, B, C…).
Essas letras são acompanhadas por índices (m e n), que contém uma informação: o primeiro número (m) indica a quantidade total de linhas e o segundo (n) indica o número total de colunas.
Por isso, uma matriz qualquer é descrita como A (mxn).
Cada elemento de uma matriz é chamado genericamente de “a ij”. Nesse caso, “i” representa em qual linha está e o “j” representa em qual coluna se localiza.
Com essas duas informações, localizamos qual a posição do elemento na tabela.
Os números colocados dentro dela podem estar entre parêntesis ( ), colchetes [ ], chaves { } ou barras duplas II II.
Cuidado!
Se os números representados estiverem entre barras únicas I I, trata-se do determinante!
- Simples né? Há mais de 200 resumos como esse no Instagram do Beduka!
Quais são os tipos de matrizes?
Precisamos entender que existem tipos de matrizes dependendo da quantidade de colunas, linhas e dos elementos que as compõem. Portanto, as matrizes podem ser classificadas em:
- Matriz linha: sempre possui apenas 1 linha.
- Matriz coluna: sempre possui apenas 1 coluna.
- Matriz nula: todos os elementos valendo 0.
- Matriz quadrada: número de linhas é igual ao número de colunas.
- Matriz transposta: A transposta (t) de uma matriz A é uma matriz At com os mesmo elementos colocados em uma posição diferente. Se A(mxn) então At = (nxm).
- Matriz oposta: obtemos ao trocar os sinais dos elementos de uma matriz inicial.
- Matriz identidade: é sempre do tipo quadrada, a diagonal principal só tem elementos 1 e os demais números são sempre 0.
- Matriz simétrica: quando fazemos a sua transposta e o resultado é igual à matriz original.
- Matriz inversa: quando duas matrizes quadradas se multiplicam e o resultado é uma matriz identidade.
- Matriz igual: duas matrizes são iguais quando são do mesmo tipo e possuem os mesmos elementos.
Você poder ler mais sobre elas e ver exemplos no artigo completo que fizemos sobre matrizes!
Operações com matrizes
É isso mesmo! Assim como quase tudo na matemática, também podemos realizar as 4 operações fundamentais com as matrizes (adição, subtração, multiplicação e divisão)!
Como somar as matrizes?
Para realizar a soma é muito simples: somamos os elementos de mesma posição e colocamos o resultado final também na mesma posição.
Como subtrair matrizes?
Na matemática que você já conhece, sabe muito bem que realizar uma subtração é a mesma coisa que realizar uma soma com o oposto do número. Assim: 4 – 2 = 4 + (-2).
Nós usamos o mesmo princípio para fazer a subtração entre matrizes. Primeiro você encontra a matriz oposta da segunda e depois realiza a soma entre elas.
Como multiplicar matrizes?
Se multiplicarmos uma matriz por um número, basta realizar a multiplicação de cada elemento da matriz por esse mesmo número: A . 2 será cada aij . 2!
Para multiplicar uma matriz inteira pela outra é mais complexo:
A multiplicação entre duas matrizes A e B só é possível quando o número de colunas de A for igual ao número de linhas de B. Isso porque devemos multiplicar cada uma das linhas por todas as colunas.
Observe:

Exercícios de Matrizes
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Parabéns por ter lido até aqui!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1 – (UFU)
Considere a matriz :
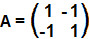
Então A4 + 2A3 + 4A2 + 8A é igual a:
a) A6.
b) A8.
c) A10.
d) A5.
Questão 2 – (PUC – RS)
O elemento c22 da matriz C = AB, onde A =

e B = :
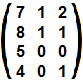
a) 0.
b) 2.
c) 6.
d) 11.
e) 22.
Questão 3 – Unicamp – 2018
Sejam a e b números reais tais que a matriz A =
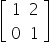
satisfaz a equação A2= aA + bI, em que I é a matriz identidade de ordem 2. Logo, o produto ab é igual a
a) −2.
b) −1.
c) 1.
d) 2.
- Você já fez 20% das questões de Matrizes. Continue assim!
Questão 4 – Unesp – 2016
Um ponto P, de coordenadas (x, y) do plano cartesiano ortogonal, é representado pela matriz coluna,
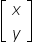
assim como a matriz coluna,
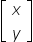
representa, no plano cartesiano ortogonal, o ponto P de coordenadas (x, y). Sendo assim, o resultado da multiplicação matricial,
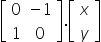
é uma matriz coluna que, no plano cartesiano ortogonal, necessariamente representa um ponto que é
a) uma rotação de P em 180º no sentido horário, e com centro em (0, 0).
b) uma rotação de P em 90º no sentido anti-horário, e com centro em (0, 0).
c) simétrico de P em relação ao eixo horizontal x.
d) simétrico de P em relação ao eixo vertical y.
e) uma rotação de P em 90º no sentido horário, e com centro em (0, 0).
Questão 5 – Unicamp – 2017
Sendo a um número real, considere a matriz A =
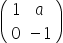
Então, A2017 é igual a
a)
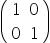
b)
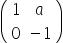
c)

d)
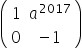
Questão 6 – (MACK)
Se A é uma matriz 3 x 4 e B uma matriz n x m, então:
a) existe A + B se, e somente se, n = 4 e m = 3;
b) existe AB se, e somente se, n = 4 e m = 3;
c) existem AB e BA se, e somente se, n = 4 e m = 3;
d) existem, iguais, A + B e B + A se, e somente se, A = B;
e) existem, iguais, AB e BA se, e somente se, A = B.
Questão 7 – (PUC)
Se A, B e C são matrizes quadradas e At, Bt e Ct são suas matrizes transpostas, e igualdade falsa entre essas matrizes é:
a) (A = B) . C = A . C + B . C.
b) (A + B)t = At + Bt.
c) (A . B)t = At . Bt.
d) (A – B)C = AC – BC.
e) (At)t = A.
- Muito bem! Você está na metade das questões sobre Matriz!
Questão 8 – (UDESC)
Sendo a matriz
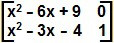
igual à matriz identidade de ordem 2, o valor de 2.x é:
a) – 4.
b) 6.
c) 4.
d) 8.
e) – 8.
Questão 9 – (PM Venda Nova do Imigrante ES – CONSULTPLAN 2016)
Calcular o valor de x+y+z, sabendo que:
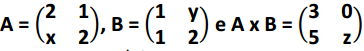
a) 1.
b) 2.
c) 3.
d) 4.
Questão 10 – (CRB – Quadrix 2014)
Na matriz A, cada elemento é obtido através de aij= 3i – j. Logo, o elemento que está na segunda linha e segunda coluna é:
a) 7.
b) 5.
c) 4.
d) 1.
e) 2.
Questão 11 – (PM Santo André – IBAM 2015)
Considere as seguintes matrizes:
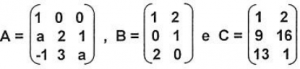
Sendo “a” um número real, para que tenhamos A . B = C, o valor da variável “a” deverá ser:
a) um número inteiro, ímpar e primo.
b) um número inteiro, par, maior que 1 e menor que 5.
c) um número racional, par, maior que 5 e menor que 10.
d) um número natural, impar, maior que 1 e menor que 5.
Questão 12 – (CRM PR – Quadrix 2014)
Uma matriz M de ordem 3 é resultante da soma de outras duas matrizes, A e B. Se aij = 2i + j e bij = ij, então a razão entre os elementos M21 e M12 é:
a) 5/6.
b) 6/5.
c) 7/4.
d) 6/7.
e) 7/5.
Questão 13 – (AGU – IDECAN 2014)
Dadas as matrizes A = ( aij)2×3 em que aij = i – j e B = ( bij)3×2 em que bij = i² – j. Seja a matriz C a matriz resultante do produto das matrizes A e B, nesta ordem. Assim, o elemento c11 será
a) 17.
b) 18.
c) 19.
d) -18.
e) -19.
- Ufa, estamos quase lá! Faça os dois últimos exercícios sobre Matrizes!
Questão 14 – (Prefeitura de Cuiabá – UFMT 2010)
Em cada um dos quatro dias de desfile de carnaval, a temperatura foi medida em graus Celsius, no meio da multidão, em três momentos distintos. Cada elemento aij da matriz A abaixo corresponde à medida da temperatura no momento i do dia j.
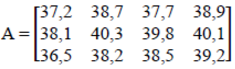
Qual foi, respectivamente, o momento e o dia em que se registrou a maior temperatura durante os desfiles?
a) 2.º e 4.º
b) 2.º e 2.º
c) 3.º e 2.º
d) 3.º e 4.º
Questão 15 – (AGU – IDECAN 2014)
Seja A uma matriz 2 x 3 e B uma matriz 3 x 2. A matriz C, resultante do produto da matriz A pela B, nesta ordem, é uma matriz de ordem
a) 2 x 2.
b) 2 x 3.
c) 3 x 2.
d) 3 x 3.
e) Não é possível fazer o produto.
- Parabéns, você fez todas as questões de Matrizes!
Respostas dos Exercícios sobre Matrizes
Exercício resolvido da questão 1 –
Alternativa correta: a) A6.
Exercício resolvido da questão 2 –
Alternativa correta: d) 11.
Exercício resolvido da questão 3 –
Alternativa correta: a) −2.
Exercício resolvido da questão 4 –
Alternativa correta: b) uma rotação de P em 90º no sentido anti-horário, e com centro em (0, 0).
Exercício resolvido da questão 5 –
Alternativa correta: b)
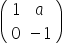
Exercício resolvido da questão 6 –
Alternativa correta: c) existem AB e BA se, e somente se, n = 4 e m = 3.
Exercício resolvido da questão 7 –
Alternativa correta: c) (A . B)t = At . Bt.
Exercício resolvido da questão 8 –
Alternativa correta: d) 8.
Exercício resolvido da questão 9 –
Alternativa correta: c) 3.
Exercício resolvido da questão 10 –
Alternativa correta: c) 4.
Exercício resolvido da questão 11 –
Alternativa correta: a) um número inteiro, ímpar e primo.
Exercício resolvido da questão 12 –
Alternativa correta: e) 7/5.
Exercício resolvido da questão 13 –
Alternativa correta: e) -19.
Exercício resolvido da questão 14 –
Alternativa correta: b) 2.º e 2.º
Exercício resolvido da questão 15 –
Alternativa correta: a) 2 x 2.
Gostou dos nossos exercícios de Matrizes?Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, mensalidade e muito mais.
Experimente agora!





