Matriz: entenda o que é, como resolver e seus tipos!

Matriz é o nome que damos a uma representação matemática das tabelas, assim, uma tabela desenhada pode ser estruturada usando uma expressão matemática. Portanto, uma matriz A (mxn) indica que ela possui “m” linhas e “n” colunas.

Neste artigo, você encontrará:

1. O que é e para quê serve
2. Representação daz matrizes, elementos e leitura
3. Quais são os tipos de matrizes: nula, quadrada, inversa, oposta, transposta, identidade
4. Operações com matrizes: adição, subtração e multiplicação

• Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!

O que é uma matriz?

Matriz é o nome que damos a uma representação matemática das tabelas. Isso significa que uma tabela desenhada pode ser estruturada de forma mais simples, usando uma expressão matemática.

Portanto, as matrizes são organizadas em linhas no formato m x n. Assim, “m” indica o número de linhas (horizontal) e “n” indica o número de colunas (vertical). 

Muitos alunos a temem, mas ela é apenas uma tabela em que as próprias posições transmitem informações. Para saber ler suas “entrelinhas”, precisamos estudar seus elementos! Veremos tudo isso nos tópicos adiante!

• Você é uma daquelas pessoas que tem fome de conhecimento? Então siga o Beduka no Instagram para conteúdos diários.

Para que servem as matrizes?

Muito além da matemática algébrica, a matriz é utilizada no mundo das finanças e economias, na engenharia, na física e até mesmo na geometria analítica! Inclusive, podemos usá-la para a resolver sistemas de equações lineares.

Se você souber como usá-la, ela pode se tornar um grande atalho nas diversas situações da vida. 

Além disso, se você é aluno, é importante conhecer tudo o que colocamos neste artigo! Isso porque essa matéria é cobrada no Ensino Médio e nos vestibulares!

Representação das matrizes

As matrizes são sempre representadas por letras maiúsculas (A, B, C…). 

Essas letras são acompanhadas por índices (m e n), que contém uma informação: o primeiro número (m) indica a quantidade total de linhas e o segundo (n) indica o número total de colunas.

Por isso, uma matriz qualquer é descrita como A (mxn).

Os números colocados dentro dela podem estar entre parêntesis ( ), colchetes [  ], chaves { } ou barras duplas II II. 

Exemplo: 

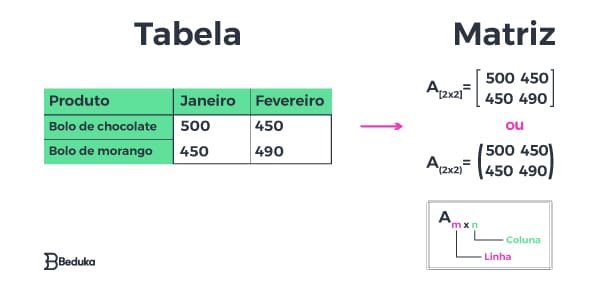
Na imagem acima, há uma tabela com os valores arrecadados na venda de bolos no primeiro bimestre do ano. 

Essa tabela apresenta dados em duas linhas (tipos de bolo) e duas colunas (meses do ano) e, por isso, trata-se de uma matriz A(2×2).

Cuidado! 

Se os números representados estiverem entre barras únicas I I, trata-se do determinante!

Como fazer matrizes? (elementos e leitura)

Nós dissemos acima que precisamos saber ler as matrizes. Isso porque as matrizes são organizadas de maneira lógica para facilitar a consulta das informações.

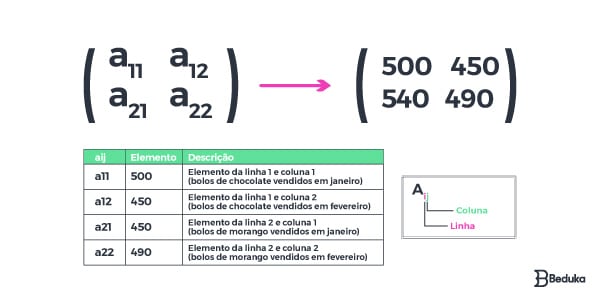
Cada elemento de uma matriz é chamado genericamente de “a ij”. Nesse caso, “i” representa em qual linha está e o “j” representa em qual coluna se localiza. 

Com essas duas informações, localizamos qual a posição do elemento na tabela.

Supondo que nós apenas olhamos a A(2×2) do tópico anterior, sem ter visto a tabela. Mas lemos que ela se refere à venda de bolos de chocolate e morango no primeiro bimestre.

Só com essas informações e observando a posição dos números, poderíamos afirmar que o número “450” se refere aos bolos de morango vendidos em janeiro.

Isso porque o “450” está na posição do elemento aij = a21. Ou seja, segunda linha (morango) e primeira coluna (janeiro).

Exemplo resolvido com lei de formação

1. Determine A = [a_ij ]_2×2, que possui a seguinte lei de formação a_ij = j² – 2i. 

Resolução:

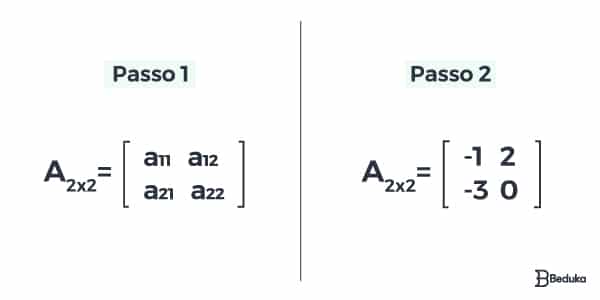
Passo 1: Dos dados do enunciado, temos que a matriz A é de ordem dois por dois, ou seja, possui duas linhas e duas colunas, logo chegamos a primeira imagem acima.

Passo 2: Além disso, foi dada a lei de formação da matriz, ou seja, a cada elemento satisfaz-se a relação a_ij = j² – 2i. Substituindo os valores de i e j na fórmula, temos:

a₁₁ = (1)² – 2(1) = -1

a₁₂ = (2)² – 2(1) = 2

a₂₁ = (1)² – 2(2) = -3

a₂₂ = (2)² – 2(2) = 0

Portanto, a matriz A corresponde à segunda imagem acima.

Quais são as matrizes? (Tipos)

Precisamos entender que existem tipos de matrizes dependendo da quantidade de colunas, linhas e dos elementos que as compõem. Portanto, as matrizes podem ser classificadas em:

• Matriz linha
• Matriz coluna
• Matriz nula
• Matriz quadrada
• Matriz transposta
• Matriz oposta
• Matriz identidade
• Matriz simétrica
• Matriz inversa
• Matriz igual

Vamos entender cada um desses tipos:

Matriz linha e Matriz coluna

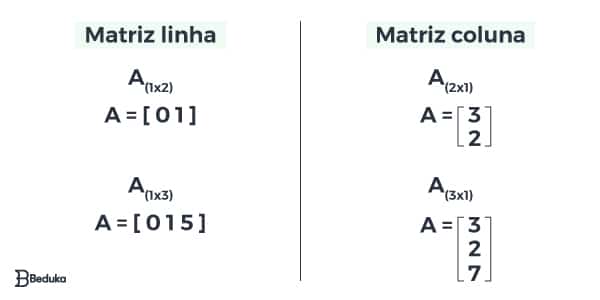
• A matriz linha é aquela que sempre possui apenas 1 linha. Isso significa que ela será do tipo A(1xn) e seus elementos a1j.

• A matriz coluna é aquela que sempre possui apenas 1 coluna. Isso significa que ela será do tipo A(mx1) e seus elementos ai1.

Matrizes nulas

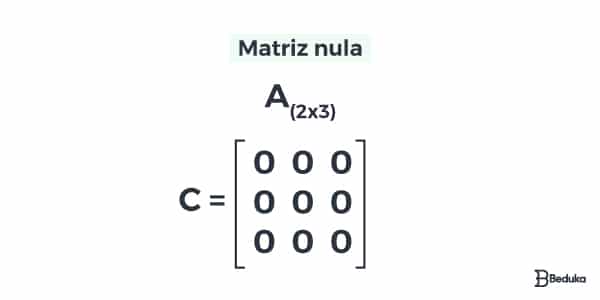
A matriz nula pode possuir quantos números forem de colunas e linhas. O que determina sua característica é possuir todos os elementos valendo 0. 

Portanto, ela é do tipo A(mxn) com todos os elementos aij = 0.

Matrizes quadradas

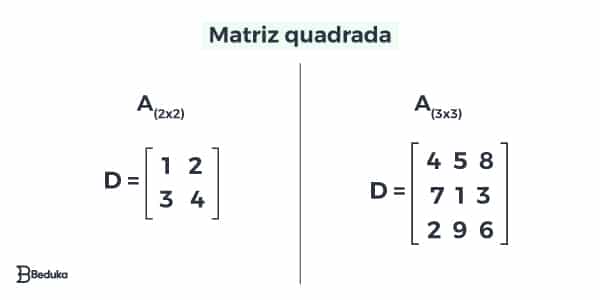
Dizemos que uma matriz é do tipo quadrada quando seu número de linhas é igual ao número de colunas. Portanto, ela é definida genericamente como A(mxm) ou A(nxn). 

Isso não interfere na representação dos elementos aij.

Igualdade de Matrizes

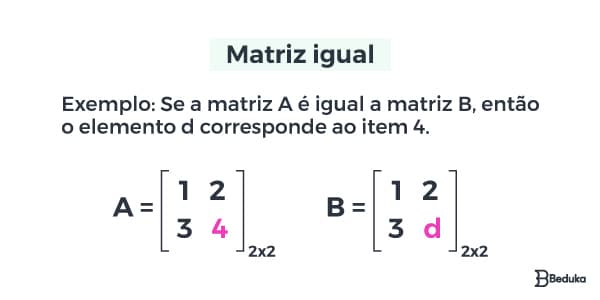
Dizemos que duas matrizes são iguais quando são do mesmo tipo e possuem os mesmos  elementos. 

Isso ocorre quando uma é uma réplica da outra, e nos ajuda a achar elementos faltantes.

Matriz identidade

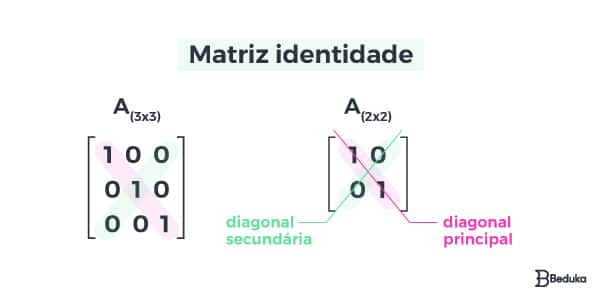
A matriz identidade é sempre do tipo quadrada e também é aquela em que a diagonal principal é toda formada por elementos que valem 1. Os demais números são sempre nulos 0.

A matriz identidade é indicado por In, onde o “n” corresponde a ordem, ou seja, seu número de colunas e linhas. Portanto, se ela tiver quatro linhas e 4 colunas, será chamada de matriz identidade de ordem 4.

A diagonal principal é formada por elementos que possuem índices iguais (todo elemento aij com i = j). A diagonal secundária é formada por elementos aij com i + j = n +1, em que n é ordem.

Propriedade:

• A matriz identidade é neutra, ou seja, qualquer matriz multiplicada pela identidade resulta na inicial: A . In = 1 . A = A.

Matrizes transpostas

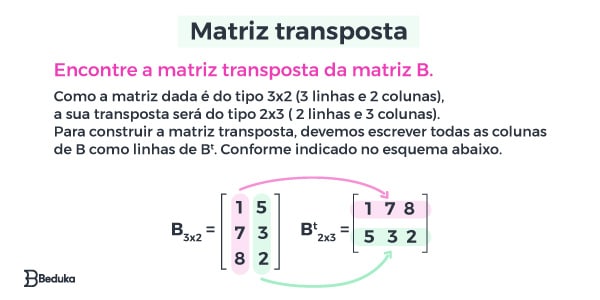
A transposta (t) de uma matriz A é uma matriz At que apresenta os mesmos elementos de A, só que colocados em uma posição diferente. Se A(mxn) então At = (nxm).

A Transposta é aquela que obtemos quando fazemos uma troca ordenada, transportando os elementos das linhas de A para as colunas da transposta At.

Exemplo

Para enxergar o que estamos dizendo, você precisa ter uma boa visão espacial! 

Propriedades:

• (At)t = A: essa propriedade indica que a transposta de uma transposta é a original.
• (A + B)t = At + Bt: a transposta da soma duas matrizes é igual a soma da transposta de cada uma delas.
• (A . B)t = Bt . At: a transposta da multiplicação de duas matrizes é igual ao produto das transpostas de cada uma delas, em ordem inversa.
• det(M) = det(Mt): o determinante da transposta é igual ao determinante da original.

Matriz simétrica

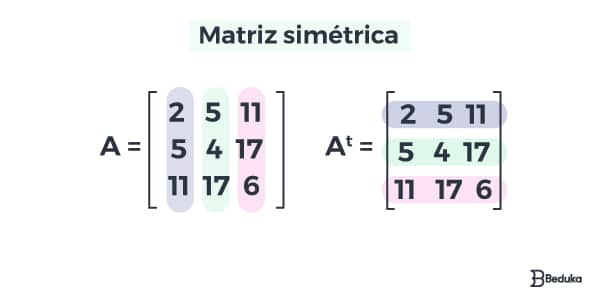
Uma matriz é chamada de simétrica quando fazemos a sua transposta e o resultado é igual à matriz original! 

Assim, a igualdade aij = aji é verdadeira se compararmos qualquer elemento das matrizes A e At, pois A = At.

Isso só ocorre em matrizes quadradas.

Matrizes opostas

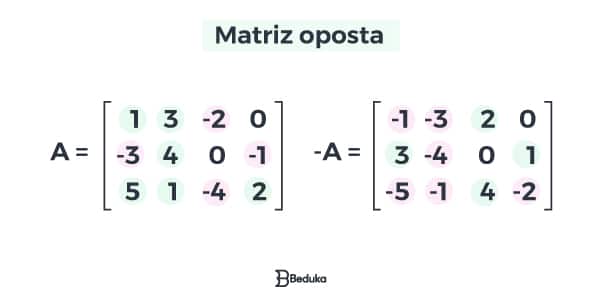
A matriz oposta é aquela que obtemos ao trocar os sinais dos elementos de uma matriz inicial.

Propriedade:

• A soma de uma matriz com a sua oposta resulta em uma matriz nula.

Matrizes inversas

Só podemos falar em matrizes inversas quando estamos analisando 2 matrizes quadradas de mesma ordem (A e B). Quando as multiplicamos, gera uma matriz identidade.

Ou seja: A . B = B . A = In

Embora a multiplicação ocorra entre duas matrizes diferentes (A e B), costumamos usar a notação B e B-1 para evidenciar que são inversas.

No último tópico deste artigo explicamos como realizar operações com matrizes.

Propriedades:

• Existe somente uma inversa para cada matriz
• Nem todas as matrizes possuem uma inversa. Só terá quando os produtos de matrizes quadradas resultam na identidade (In)
• A matriz inversa de uma inversa corresponde à própria matriz: A = (A-1)-1
• A matriz transposta de uma inversa também é inversa: (At) -1 = (A-1)t
• A matriz inversa de uma transposta corresponde à transposta da inversa: (A-1 At)-1
• A matriz inversa de uma matriz identidade é igual à matriz identidade: I-1 = I

Como realizar operações com matrizes?

É isso mesmo! Assim como quase tudo na matemática, também podemos realizar as 4 operações fundamentais com as matrizes (adição, subtração, multiplicação e divisão)! 

Fique atento às explicações a seguir para entender como fazer isso:

Adição de matrizes

Para realizar a soma é muito simples: somamos os elementos de mesma posição e colocamos o resultado final também na mesma posição.

Observe a imagem acima para ver o exemplo numérico! 

Propriedades

• Comutativa: trocar a ordem dos fatores não altera o resultado. A + B = B + A
• Associativa: trocar a ordem das somas não altera o resultado. A + (B + C) = (A + B) + C 
• Elemento oposto: somar matrizes opostas resulta em matrizes nulas. A + (-A) = 0
• Elemento neutro: somar matrizes com um elemento neutro resulta nas próprias matrizes iniciais. A + 0 = A

Subtração de matrizes

Na matemática que você já conhece, sabe muito bem que realizar uma subtração é a mesma coisa que realizar uma soma com o oposto do número. Assim: 4 – 2 = 4 + (-2). 

Nós usamos o mesmo princípio para fazer a subtração entre matrizes. Primeiro você encontra a matriz oposta da segunda e depois realiza a soma entre elas.

Multiplicação de matrizes

A multiplicação entre duas matrizes A e B só é possível quando o número de colunas de A for igual ao número de linhas de B. Isso acontece porque o método de multiplicação exige isso:

Para efetuar a multiplicação entre as matrizes, devemos multiplicar cada uma das linhas por todas as colunas. 

Assim, o primeiro elemento de A é multiplicado pelo primeiro elemento de B e, em seguida, somado ao segundo elemento de A  multiplicado pelo segundo elemento de B. Assim prosseguimos sucessivamente.

Observe a imagem acima atentamente, guiando-se pelas cores!

Multiplicação por um número real: Se multiplicarmos uma matriz por um número, basta realizar a multiplicação de cada elemento da matriz por esse mesmo número: A . 2 será cada aij . 2!

Propriedades

• Associativa: em multiplicações sucessivas, alterar a ordem não interfere no resultado. A . (C . B) = (A . B) . C
• Distributiva: A . (B + C) = A . B + A . C
• Elemento neutro: Multiplicar por uma matriz identidade é o mesmo que multiplicar por 1: A . In = A

Gostou do nosso artigo? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet.