Na matemática, o sistema de equações é uma forma de encontrar a solução para equações com mais de uma incógnita. Para isso, é preciso duas ou mais equações, com o mesmo conjunto de incógnitas. O método pode ser o da adição ou subtração, buscamos uma mesma solução que sirva para todas as equações envolvidas.
Neste artigo sobre sistema de equações, você encontrará:
- Introdução: relembrando o que é uma equação
- O que é um sistema de equações e como resolvê-lo
- Método da Adição e da Substituição
- Classificação dos sistemas
- Dúvidas comuns: sistema de 3 equações e de 2° grau
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
Introdução: relembrando o que é uma equação
Antes de falar sobre sistemas de equações, precisamos relembrar o que são as Equações. Se você quiser um artigo completo sobre Equações de Primeiro e Segundo grau, está na mão! Mas se não tem tempo agora, relembre os conceitos básicos a seguir:
- A fórmula base para qualquer equação do 1° com uma incógnita é ax + b = 0. Nela, o x é a nossa incógnita, o “a” é o coeficiente e o “b” é um termo independente.
- O nosso objetivo é achar quanto vale a incógnita (x). Ao colocarmos um número no lugar do x, o resultado da conta da equação precisa ser zero.
- O lado esquerdo de uma igualdade é chamado de 1º membro da equação e o lado direito é chamado de 2º membro. Equação significa igualdade.Tanto o lado esquerdo do =, quanto o lado direito, tem que apresentar o mesmo resultado.
Para resolvê-la, basta aplicar os 4 passos que explicamos no artigo das equações:
1.Eliminar os parênteses fazendo as operações prioritárias
2.Efetuar a transposição de termos
3.Reduzir os termos semelhantes
4.Isolar a incógnita e encontrar seu valor numérico
Como resolver uma equação de 1° grau com duas incógnitas?
Uma equação de 1° grau com duas incógnitas é baseada na expressão ax + by = c (onde a e b são ≠ 0, c ∈ R).
Para resolvê-la, precisamos de uma outra equação com incógnitas iguais. Assim será possível construir um sistema para compará-las e encontrar valores que satisfaçam ambas ao mesmo tempo.
Essa outra equação não pode ser inventada, ela precisa estar relacionada com a original e ser proporcional. A própria questão te dará informações suficientes para montar 2 equações ou mais!
Veremos exemplos a seguir!
O que é sistema de equações lineares? Exemplos
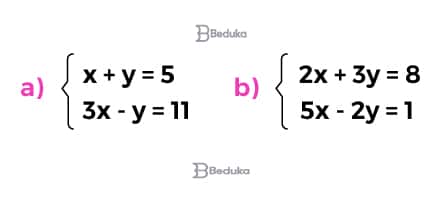
Note que cada equação possui duas incógnitas diferentes dentro delas: x e y. Porém, a equação de baixo possui as mesmas duas incógnitas x e y, mas tem números diferentes. Por isso, não podemos resolvê-las de forma isolada.
Qual é o segredo? Formar um sistema para encontrar uma outra equação que tenha as mesmas incógnitas x e y. Ela deve surgir da mistura das duas primeiras.
O sistema será do tipo linear quando possuir apenas equações de 1° grau, não havendo incógnita elevada ao quadrado ou a qualquer outro número. Sempre que uma letra está escrita na equação sem números no expoente, significa que há o número 1 ali. Isso significa que é de primeiro grau.
- Como você viu acima, eles sempre serão utilizados como uma ferramenta para resolver problemas em que há equações com mais de uma incógnita.
Com ele é possível encontrar os valores que satisfaçam simultaneamente todas as equações por meio da comparação matemática. Aprenderemos como fazer isso à frente!
Como resolver um sistema de equações?
Para resolver um sistema de equações, é necessário encontrar os valores que satisfaçam todas as equações ao mesmo tempo. Para isso, podemos usar dois métodos diferentes: o método da substituição ou o da adição.
Ambos são corretos e você pode escolher o que for mais fácil. Mas fique atento porque cada um pode ser melhor para uma determinada situação! Nos tópicos a seguir, daremos a explicação e o exemplo das duas formas separadamente.
- Tenha em mente que partimos da seguinte lógica (nos dois métodos):
Se não conseguimos trabalhar com duas incógnitas ao mesmo tempo, o melhor jeito é fazer uma delas “sumir” temporariamente. Assim, primeiro calculamos o valor de uma e depois resgatamos a outra para descobrir o seu valor também.
Método da Adição – Passo a passo

No método da adição, buscamos somar as duas equações para que resultem em uma única, ao mesmo tempo em que eliminamos uma das incógnitas.
- Você deve escolher uma incógnita para sair de cena. No exemplo da imagem acima, escolhemos o Y. Como fazer isso?
- Em uma adição, as coisas só “somem” quando são perfeitamente opostas. Isso significa que o coeficiente (número que acompanha a letra) precisa ser o mesmo. Também é preciso que cada um deles tenha um sinal diferente (positivo e negativo).
- Um Y tinha coeficiente +1 e outro era +3. Para que fiquem opostos, escolhemos o +Y para multiplicar por -3. Assim, temos o resultado que queríamos: +3 em uma equação e -3 em outra.
- Lembre-se: só podemos multiplicar ou dividir uma incógnita se fizermos o mesmo com toda a equação. Isso garante que o resultado dela será o mesmo, porque os números mudaram de forma proporcional.
- Realizando a soma entre a primeira equação e a segunda (depois da modificação), o termo Y irá se anular e sumir. Os outros, somamos normalmente.
- O resultado disso será uma nova equação com apenas uma incógnita, a X. Você já sabe como resolver uma equação com uma incógnita, como mostramos no artigo de Equação linear.
- Agora que já descobriu quanto vale o X, você pode escolher qualquer uma das duas equações antigas para colocar o valor numérico no lugar do X.
- Novamente, você terá uma equação com uma incógnita: a Y. Agora você pode resolver normalmente e descobrir o valor que faltava.
Por isso, esse método é indicado para os casos em que uma das incógnitas aparece na primeira equação com valor positivo e na segunda com valor negativo. Ou ainda para qualquer caso em que um dos termos é múltiplo do da outra.
Se as coisas não estiverem dispostas dessa forma e mesmo assim você quiser utilizar o método, basta fazer a multiplicação de toda uma equação para que fique da forma necessária.
Método da Substituição – Passo a passo
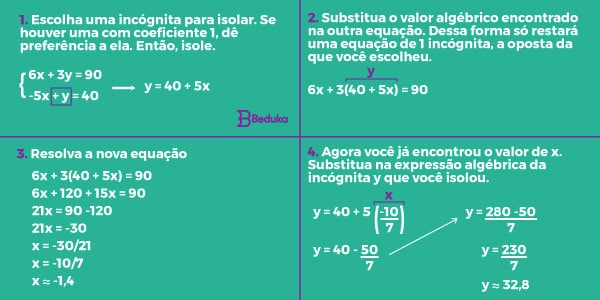
No método da substituição, vamos isolar uma incógnita no primeiro membro de uma das equações. Isso nos dará uma nova equação, ao mesmo tempo em que eliminamos uma das incógnitas.
- Você deve escolher uma incógnita para sumir. Como? No exemplo da imagem acima, escolhemos o Y e o colocamos sozinho no primeiro membro. Todo o resto da equação deve ser passado ao segundo membro, sempre com sinal contrário.
- Por ser uma igualdade, significa que tudo o que está no segundo membro representa o valor de Y.
- Agora, você pode pegar a segunda equação que ainda não foi mexida. Nela, você vai retirar o Y e, no lugar, colocar o valor que você encontrou quando o isolou.
- Assim, você tem uma equação formada por uma incógnita e pode resolver normalmente para descobrir o valor do que restou, o X!
- Tendo o valor numérico de X, só nos resta descobrir o do Y.Note que, quando você isolou o Y, a expressão encontrada para representar seu valor tinha um X no meio.
- Então, basta colocar o valor numérico no lugar do X e teremos outra equação de uma incógnita. Resolvendo normalmente, encontramos o valor que faltava para Y.
Este método é indicado para qualquer caso! Mas fique atento, a expressão formada pela substituição pode gerar uma equação de segundo grau ou um número maior. Se tiver pouco tempo para resolver, opte pelo outro método.
Classificação dos sistemas de equações
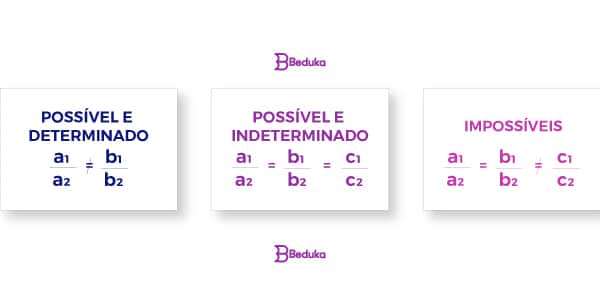
Além de poder ser quadrático ou linear, eles podem ser classificados conforme a possibilidade e quantidade de soluções.
Imagine um sistema linear formado pelas equações a1x + b1y = c1 e a2x + b2y = c2. Esse sistema pode ser classificado como possível e determinado, possível e indeterminado e impossível.
- Será possível e determinado quando apresentar uma única solução. Você pode descobrir isso resolvendo o sistema, mas um jeito fácil de saber é pela “colinha” da imagem acima.
- Possível e indeterminado é para quando o sistema apresentar infinitas soluções. A condição para você identificar um sistema desse tipo, sem ter que resolver, está apresentada na imagem acima!
- Já os sistemas impossíveis, não possuem nenhuma solução. Nesse tipo de sistema podemos verificar a relação da imagem logo aí acima!
Dúvidas comuns e outros exemplos de sistema de equações!
Mesmo entendendo as explicações do que é mais comum, a criatividade dos professores vai longe e você pode se deparar com algo que ainda não viu.
Por isso, nós do Beduka trouxemos as 2 outras situações que podem te causar estranheza, mas que são possíveis! Veja:
O que é sistema de equação do 2 grau? Como resolver?

Embora o sistema linear seja o mais comum, podem existir outros tipos! Quando um sistema de equações é formado por equações de 2° grau, ele é chamado de sistema de equações do tipo quadrático ou sistema de equação do 2° grau.
- Como você viu acima, independente do tipo, eles sempre serão utilizados como uma ferramenta para resolver problemas em que há equações com mais de uma incógnita.
Podemos resolver um sistema quadrático da mesma forma que o linear. A única diferença é que ele pode vir a ter até 4 soluções. Mas isso não influencia no modo de resolução.
Observe a imagem acima para ter um exemplo!
Como resolver um sistema de 3 equações?
Um sistema de equações pode ser formado por 2 ou mais equações e incógnitas. Porém, só será possível resolvê-los se o número de incógnitas for igual ao número de equações. Então bastará aplicar os métodos de resolução que já conhecemos: substituição ou adição.
Neste caso, é sugerido optar pelo da substituição, pois basta escolher uma equação e isolar uma incógnita. Depois, substituímos a expressão encontrada nas outras duas equações.
Ao reduzir os termos semelhantes, restarão duas equações com duas incógnitas, então basta resolvê-las como um sistema normal!
ATENÇÃO! Não se esqueça de, após encontrar os valores das duas incógnitas, voltar na primeira equação e substituir os números para encontrar o valor da terceira incógnita!
Gostou do nosso artigo sobre sistema de equações? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!






2 Comentários
É a primeira vez que visito esse blog
E pela qualidade do mesmo me sinto no dever de dizer que a experiência foi muito boa.
Aqui os contéudo são mais resumido, dando assim a total compreensão para o leitor!
Não sou muito bom com as palavras e nem com as escritas, por isso por agradecer os dirigentes do mesmo!
Sempre estamos tentando melhorar a experiência de quem nos acompanha, Afonso. Volte sempre!