Se um sólido geométrico for atravessado por um plano, dependendo do ângulo e do sólido, surgirão figuras. No caso do cone duplo de revolução, surgem 4 formas chamadas de Cônicas: circunferência, hipérbole, parábola e elipse. Leia o resumo e resolva os exercícios sobre Cônicas, com o gabarito no final!
Quer seguir diretamente para alguma parte? Clique em um dos tópicos abaixo:
- O que são Cônicas?
- Quais são as fórmulas da Circunferência?
- Como são as Elipses?
- O que são Parábolas na matemática?
- Quais são as características da Hipérbole?
- Os 10 melhores exercícios sobre Cônicas!
- Gabarito das questões sobre Cônicas.
Quando você terminar os exercícios de Cônicas, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil!
O que são Cônicas?
Cônicas são simplesmente as figuras planas que vêm do Cone, quando atravessamos um plano por esse sólido geométrico.
É como se pegássemos uma lâmina e fizéssemos cortes em diferentes ângulos. Cada corte que for feito com certa inclinação irá formar uma figura na superfície, essas são as Cônicas.
Em cada sólido, podemos encontrar diferentes formatos. No caso dos cones, há 4 possibilidades:
- Circunferências;
- Elipses;
- Parábolas;
- Hipérboles.
São mais de 200 resumos no instagram do Beduka, confira!
Quais as características e fórmulas das Cônicas?
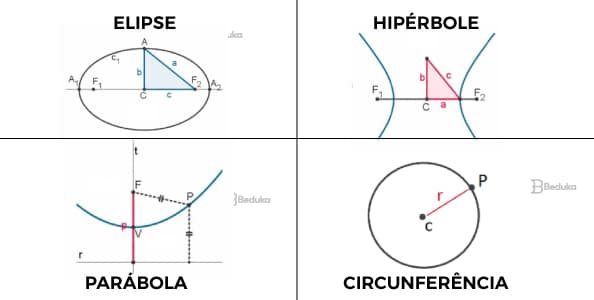
Nós já fizemos um artigo completo sobre o que são Cônicas. Nele, você encontra as explicações detalhadas, que são ótimas para quem ainda não entendeu esse assunto.
Agora, vamos apenas resumir as partes principais, para ajudar a fazer os exercícios:
Como são as Circunferências?
Definição de Circunferência:
Figura plana formada por um ponto central (C) cercado por todos os pontos que estão a uma mesma distância. Essa distância é chamada de raio (r).
O que precisamos saber para realizar os cálculos são as fórmulas da Geometria Analítica. A principal delas é a equação reduzida da circunferência:
(x – a)² + (y – b)² = r²
Em que:
- (a, b) = coordenadas do ponto C;
- (x, y) = coordenadas do ponto P, qualquer um que pertença à circunferência;
- r = raio.
Ela é a fórmula que nos dará as informações sobre a figura, como representá-la em um plano cartesiano e suas medidas.
Quais são as características das Elipses?
Definição de Elipse:
Dados os pontos F1 e F2, a elipse é o conjunto de pontos P em que vale a seguinte expressão:
dPF1 + dPF2 = 2a
Para realizar os cálculos, precisamos conhecer as duas equações reduzidas.
- A primeira é válida para quando os focos estão sobre o eixo das abscissas (x, horizontal) e o centro sobre a origem de um plano cartesiano:
x²/a² + y²/b² = 1
- A segunda é para os casos em que os vértices da elipse estão sobre o eixo das coordenadas (y, vertical) e seu centro sobre a origem do plano:
y²/a² + x²/b² = 1
Em que x e y são as coordenadas de um ponto pertencente. As leis da Gravitação Universal, propostas por Kepler, se baseiam nessa figura.
O que é uma Parábola na matemática?
Definição de Parábola:
Dada uma parábola de foco F e uma reta r abaixo dela, cada um de seus pontos (P) apresentam uma distância própria até F que é igual até r.
dPF = dPr
A reta “t” é o eixo de simetria da parábola e, dependendo de sua posição, pode nos dar duas equações gerais:
- Se coincidir com o eixo x do plano e o vértice (V) estiver na origem do plano, a equação reduzida da parábola será:
y² = 2px
- Se seu eixo de simetria estiver sobre o eixo y e o vértice na origem do plano, a equação reduzida da parábola será:
x² = 2py
Em que x e y são as coordenadas de um ponto pertencente. Sua representação é o gráfico da função de 2° grau!
Como são as Hipérboles?
Definição de hipérbole:
Conjunto de pontos do plano cuja diferença das distâncias até os focos é igual à constante 2a. Assim, se P é um ponto da hipérbole, vale a expressão modular:
|dPF1 – dPF2| = 2a
As equações reduzidas da hipérbole também são duas:
- A primeira para quando os focos estão sobre o eixo x e o centro coincide com a origem do plano cartesiano:
x²/a² + y²/b² = 1
- A segunda é para quando os focos estão sobre o eixo y e o centro coincide com a origem do plano cartesiano:
y²/a² + x²/b² = 1
Em que x e y são as coordenadas de um ponto pertencente. O gráfico da função exponencial é um braço de hipérbole!
Os 10 exercícios sobre Cônicas!
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Obrigado por ter lido até aqui!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1- (UFF 1997)
As equações y – 2x = 0, y + x² = 0 e y² – x² + 1 = 0 representam no plano, respectivamente:
a) uma reta, uma hipérbole e uma parábola.
b) uma parábola, uma hipérbole e uma reta.
c) uma reta, uma parábola e uma elipse.
d) uma elipse, uma parábola e uma hipérbole.
e) uma reta, uma parábola e uma hipérbole.
Questão 2- (UFAM)
Os pontos A(4, 0) e B(0, 6) são extremos de um diâmetro da circunferência. Então, a equação reduzida da circunferência é:
a) x² + y² – 6x – 4y = 0.
b) x² + y² – 4x – 6y = 0.
c) x² + y² + 4x – 6y = 0.
d) x² + y² + 4x + 6y = 0.
e) x² + y² – 6x + 4y = 0.
- Você já fez 20% das questões sobre Cônicas. Continue assim!
Questão 3- (PUC-MG 2006)
A figura a seguir representa o corte plano de uma pista de skate, cuja equação é y = ax².
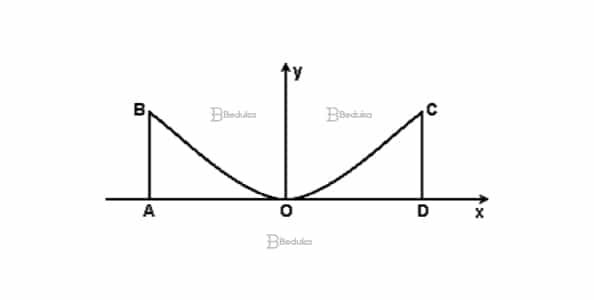
Considerando-se AO = OD = 5 m e AB = DC = 4 m, pode-se afirmar que o valor do parâmetro a é:
a) 0,12.
b) 0,16.
c) 0,20.
d) 0,24.
Questão 4- (PUC-Rio)
O número de pontos de intersecção das duas parábolas y = x² e y = 2x² – 1 é:
a) 0.
b) 1.
c) 2.
d) 3.
e) 4.
Questão 5- (ENEM 2017)
O fisiologista inglês Archibald Vivian Hill propôs, em seus estudos, que a velocidade v de contração de um músculo ao ser submetido a um peso p é dada pela equação (p + a)(v + b) = K com a, b e K constantes.
Um fisioterapeuta, com o intuito de maximizar o efeito benéfico dos exercícios que recomendaria a um de seus pacientes, quis estudar essa equação e a classificou desta forma:
Tipo de curva
Semirreta oblíqua
Semirreta horizontal
Ramo de parábola
Arco de circunferência
Ramo de hipérbole
O fisioterapeuta analisou a dependência entre v e p na equação de Hill e a classificou de acordo com sua representação geométrica no plano cartesiano, utilizando o par de coordenadas (p;v). Admita que K>0.
Disponível em: http:?/rspb.royalsocietypublishing.org. Acesso em: 14 jul. 2015 (adaptado).
O gráfico da equação que o fisioterapeuta utilizou para maximizar o efeito dos exercícios é do tipo
a) semirreta oblíqua.
b) semirreta horizontal.
c) ramo de parábola.
d) arco de circunferência.
e) ramo de hipérbole.
- Nossa! Você já fez metade das questões de Cônicas. Vamos lá!
Questão 6- (UFPB 2011)
A secretaria de infraestrutura de um município contratou um arquiteto para fazer o projeto de uma praça. Na figura a seguir, está o esboço do projeto proposto pelo arquiteto: uma praça em formato retangular medindo 80 m x 120 m, onde deverá ser construído um jardim em forma de elipse na parte central.
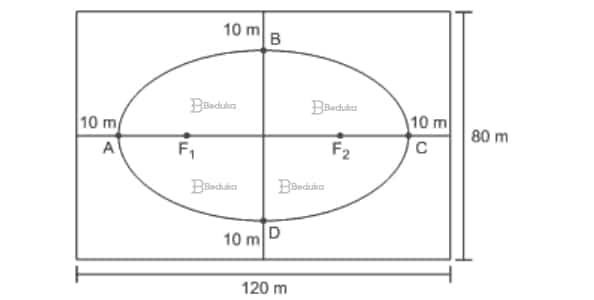
Estão destacados na figura os segmentos AC e BD que são, respectivamente, o eixo maior e o menor da elipse, bem como os pontos F1 e F2, que são os focos da elipse onde deverão ser colocados dois postes de iluminação.
Com base nessas informações, conclui-se que a distância entre os postes de iluminação será, aproximadamente, de:
a) 68 m.
b) 72 m.
c) 76 m.
d) 80 m.
e) 84 m.
Questão 7- (FGV 2013)
Sendo “m” o maior valor real que x pode assumir na equação analítica (x – 2)² + 4(y + 5)² = 36 e “n” o maior valor real que y pode assumir nessa mesma equação, então, m+n é igual a:
a) 8.
b) 7.
c) 6.
d) 4.
e) 3.
Questão 8- (UFPI 2000)
O gráfico da equação x² – y² = 4 representa uma hipérbole. Os focos dessa hipérbole são:
a) (½ , 0) e (-½ , 0).
b) (2 , 0) e (-2 , 0).
c) (2√2 , 0) e (-2√2 , 0).
d) (0 , √2) e (0 , -√2).
e) (0 , ½) e (0 , -½).
- Ufa! Agora só faltam mais dois exercícios de Cônicas!
Questão 9- (UFRN)
O conjunto dos pontos P = (x,y), que estão a uma mesma distância do ponto F = (0,2) e do eixo ox, no plano cartesiano xy é
a) a parábola de equação y = (x²/2) + 4.
b) a parábola de equação y = (x²/4) + 1.
c) a parábola de equação y = 4x² +1.
d) a parábola de equação y = 2x² +1.
Questão 10- (ENEM 2013)
Durante uma aula de Matemática, o professor sugere aos alunos que seja fixado um sistema de coordenadas cartesianas (x, y) e representa na lousa a descrição de cinco conjuntos algébricos, I, II, III, IV e V, como se segue:
I — é a circunferência de equação x² + y² = 9;
II — é a parábola de equação y = − x² − 1, com x variando de −1 a 1;
III — é o quadrado formado pelos vértices (−2, 1), (−1, 1), (−1, 2) e (−2, 2);
IV — é o quadrado formado pelos vértices (1, 1), (2, 1), (2, 2) e (1, 2);
V — é o ponto (0, 0).
A seguir, o professor representa corretamente os cinco conjuntos sobre uma mesma malha quadriculada, composta de quadrados com lados medindo uma unidade de comprimento, cada, obtendo uma figura.
Qual destas figuras foi desenhada pelo professor?
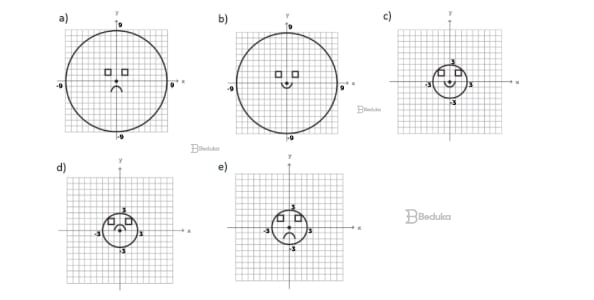
- Parabéns, você fez todos os exercícios sobre Cônicas. Confira agora o Gabarito:
Gabarito das questões sobre Cônicas
Exercício resolvido da questão 1 –
Alternativa correta: e) uma reta, uma parábola e uma hipérbole.
Exercício resolvido da questão 2 –
Alternativa correta: b) x2 + y2 – 4x – 6y = 0.
Exercício resolvido da questão 3 –
Alternativa correta: b) 0,16.
Exercício resolvido da questão 4 –
Alternativa correta: c) 2.
Exercício resolvido da questão 5 –
Alternativa correta: e) ramo de hipérbole.
Exercício resolvido da questão 6 –
Alternativa correta: d) 80 m.
Exercício resolvido da questão 7 –
Alternativa correta: c) 6.
Exercício resolvido da questão 8 –
Alternativa correta: c) (2√2 , 0) e (-2√2 , 0).
Exercício resolvido da questão 9 –
Alternativa correta: b) a parábola de equação y = (x²/4) + 1.
Exercício resolvido da questão 10 –
Alternativa correta: e) (imagem).
- Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos exercícios sobre Cônicas? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.





