Se um sólido geométrico for atravessado por um plano, dependendo do ângulo e do sólido, surgirão figuras planas. No caso do cone duplo de revolução, surgem 4 formas chamadas de Cônicas: circunferência, hipérbole, parábola e elipse. Elas são usadas em várias áreas, então é bom saber o que são cônicas e as suas fórmulas!
Neste resumo sobre o que são Cônicas, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:
- O que são Cônicas? Exemplos!
- Para que servem as Cônicas?
- Curiosidade: de onde surgiram as Cônicas?
- Como são as Circunferências?
- Quais são as características das Elipses?
- O que é uma Parábola na matemática?
- O que são as Hipérboles?
Depois você pode testar o que aprendeu. É só fazer o nosso Simulado ENEM gratuito! Ele pode ser personalizado com as matérias que você quiser.
O que são Cônicas?
Cônicas são simplesmente as figuras planas que vêm do Cone, quando atravessamos um plano por esse sólido geométrico.
É como se pegássemos uma lâmina e fizéssemos cortes em diferentes ângulos. As figuras que se formam na superfície do corte são as Cônicas.
Em cada sólido, podemos encontrar diferentes formatos. No caso dos cones, as possibilidades são 4: circunferências, elipses, parábolas e hipérboles.
Agora que você já entendeu a ideia central, vamos elaborar uma definição mais bonita:
“Cônicas são figuras bidimensionais encontradas na intersecção entre um plano e um cone duplo, obtido pela revolução de uma reta.”
Opa! Tem informação nova aí… O que seria um cone duplo de revolução?
Entenda:
Exemplo de cônicas obtidas em um sólido de revolução
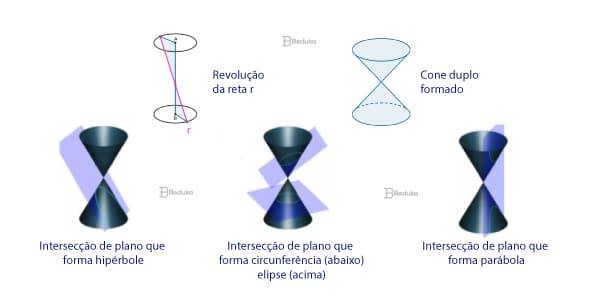
Sólido de revolução é o nome que damos às figuras tridimensionais que podemos encontrar quando giramos alguma figura plana.
Imagine um triângulo retângulo sobre um prato de decoração de bolo. Um dos catetos está apoiado na base e o outro está virado para o centro do prato. Agora, gire esse prato sem parar, em uma velocidade muito alta…
Quando você olha de longe, o vulto que se forma tem o formato de Cone!
- São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
Então, o que seria um Cone Duplo?
Para entender isso, vamos imaginar outra situação: pense em dois pratos giráveis, um acima do outro, com um espaço entre eles. Agora, coloque uma reta inclinada conectando os dois pratos e gire!
O formato que você encontrará é o de uma ampulheta, que é formada por dois cones!
Na imagem acima, você consegue entender esse processo e, também, visualizar as Cônicas quando cortamos o cone duplo com o plano. É importante que ele seja duplo para que você tenha as figuras e as suas inversões.
- Depois de tanta informação, você deve estar se fazendo uma pergunta:
Para que servem as Cônicas?
As cônicas são figuras que aparecem relacionadas a outras matérias, então servem para embasar as suas explicações. Por isso são essenciais! Sem elas, a aprendizagem dos demais assuntos seria dificultada.
- As circunferências, por exemplo, são muito usadas na Geometria Analítica, uma área da matemática que relaciona os desenhos com álgebra.
- Já as elipses aparecem na física, como parte da teoria de Kepler sobre a Gravitação Universal.
- Os arcos de parábola são os desenhos formados nos gráficos das funções de segundo grau.
- Os braços de hipérbole são os desenhos formados nos gráficos das funções exponenciais.
Curiosidade: de onde surgiram as Cônicas?
Sim, as cônicas também começaram a ser estudadas na Grécia Antiga…
E, para variar, foram os clássicos Euclides, Arquimedes e Manaecmo que começaram esse assunto de Geometria. Inclusive, este último é que descobriu as cônicas e se dedicou a estudá-las.
Reza a lenda que tudo começou porque estavam diante de um problema:
O rei Minos fez o pedido de que o túmulo de seu filho, Glauco, fosse dobrado de tamanho sem perder o formato. Após inúmeras tentativas para achar um cálculo condizente com o formato do túmulo, Menaecmo resolveu pegar um cone e fazer seções nele.
Estudando as cônicas formadas, a solução foi encontrada. Daí em diante outros problemas semelhantes tiveram solução. Mais tarde, Apolônio deu os nomes de elipse, parábola e hipérbole para as figuras.
- Agora, vamos aprender as características e fórmulas de cada figura para saber como usá-las a nosso favor!
Como são as Circunferências?
A circunferência é uma figura plana que corresponde ao contorno do círculo. Sendo assim, ela é formada por uma linha que se curva. Porém, quando lembramos das definições da geometria plana, sabemos que as linhas são o alinhamento de diversos pontos.
Seguindo esse raciocínio, completamos com a ideia de que a circunferência é definida por:
Figura formada por um ponto central (C) cercado por todos os pontos que estão a uma mesma distância dele. Essa distância é chamada de raio (r).
O que precisamos saber para realizar os cálculos é a equação reduzida da circunferência.
Assim:
(x – a)² + (y – b)² = r²
- (a, b) = coordenadas do ponto C;
- (x, y) = coordenadas do ponto P, qualquer um que pertença à circunferência;
- r = raio.
Ela é a fórmula que nos dará as informações sobre a figura, como representá-la em um plano cartesiano e suas medidas.
Note que ela segue o mesmo modelo do Teorema de Pitágoras, que é o método usado para calcular a distância entre dois pontos!
Quais são as características das Elipses?
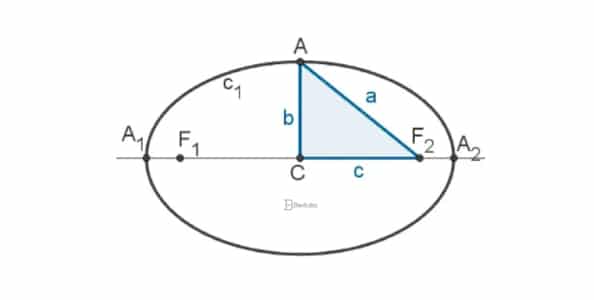
As Elipses são formatos semelhantes a uma “circunferência achatada”, melhor definido como um “oval simétrico”.
Nela, também há um ponto central C. A novidade é que ela possui “extremidades” bem definidas, marcadas pelos pontos A1 e A2 para a horizontal e o ponto A para a vertical.
Os pontos F1 e F2 são chamados de Foco e a distância entre cada um deles e o centro é a mesma (representada pela letra c). Portanto, a distância entre esses dois pontos será o dobro (2c).
Juntando as informações, podemos traçar um triângulo retângulo que liga o ponto C, o ponto A e um dos focos. Depois, completamos o desenho dando nomes aos lados formados. Se um deles já corresponde ao c, o outro é b e a hipotenusa será a.
Agora podemos entender a sua definição formal:
Dados os pontos F1 e F2, a elipse é o conjunto de pontos P em que vale a seguinte expressão:
dPF1 + dPF2 = 2a
Para realizar os cálculos, precisamos conhecer as duas equações reduzidas.
- A primeira é válida para quando os focos estão sobre o eixo das abscissas (x, horizontal) e o centro sobre a origem de um plano cartesiano:
(x²/a²) + (y²/b²) = 1
- A segunda é para os casos em que os vértices da elipse estão sobre o eixo das coordenadas (y, vertical) e seu centro sobre a origem do plano:
(y²/a²) + (x²/b²) = 1
Em que x e y são as coordenadas de um ponto pertencente.
O que é uma Parábola na matemática?
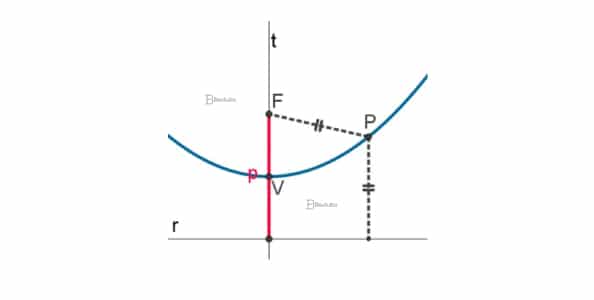
A parábola é semelhante ao formato da entrada de um túnel, sempre simétrica. É como se pegássemos uma elipse e partíssemos ao meio.
Uma definição mais formal é:
Dada uma parábola de foco F e uma reta r abaixo dela, cada um de seus pontos (P) apresentam uma distância própria até F que é igual até r.
dPF = dPr
A reta “t” é o eixo de simetria da parábola e, dependendo de sua posição, pode nos dar duas equações gerais:
- Se coincidir com o eixo x do plano e o vértice (V) estiver na origem do plano, a equação reduzida da parábola será:
y² = 2px
- Se seu eixo de simetria estiver sobre o eixo y e o vértice na origem do plano, a equação reduzida da parábola será:
x² = 2py
Em que x e y são as coordenadas de um ponto pertencente.
Como são as Hipérboles?
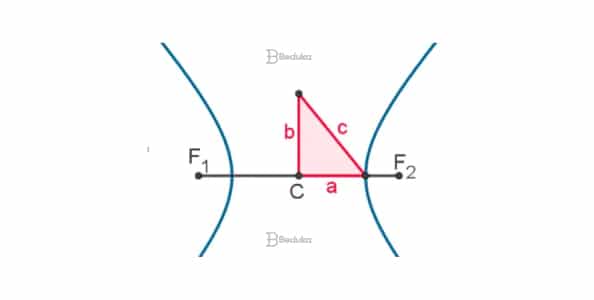
As hipérboles são figuras que possuem os focos F1 e F2. A distância de um dos focos até o centro (C) vale a. Logo, a distância entre os focos vale 2a.
Elas são mais formalmente definidas assim:
Conjunto de pontos do plano cuja diferença das distâncias até os focos é igual à constante 2a. Assim, se P é um ponto da hipérbole, vale a expressão modular:
|dPF1 – dPF2| = 2a
As equações reduzidas da hipérbole também são duas:
- A primeira para quando os focos estão sobre o eixo x e o centro coincide com a origem do plano cartesiano:
(x²/a²) + (y²/b²) = 1
- A segunda é para quando os focos estão sobre o eixo y e o centro coincide com a origem do plano cartesiano:
(y²/a²) + (x²/b²) = 1
Em que x e y são as coordenadas de um ponto pertencente.
Gostou do nosso resumo sobre o que são Cônicas? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





