Os 14 Melhores Exercícios sobre Funções com Gabarito

Na matemática, funções são regras que relacionam dois valores dependentes (x e y). Seus valores são agrupados em domínio e contradomínio e cada tipo de função possui propriedades e gráficos próprios. Neste texto você poderá testar o que sabe com alguns exercícios sobre funções. 

Quando você terminar os Exercícios sobre funções, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil. 

O que são Funções? (Definição)

Funções matemáticas são expressões numéricas e algébricas (números e letras). Elas possuem dois lados separados pelo sinal de igual (=) e obedecem uma lei de formação. 

Em um de seus lados aparece o “f(x)”, conhecido popularmente como “y”. Do outro lado, temos um conjunto de valores rodeando a incógnita “x”. Esses valores são chamados de regra matemática. 

Ser uma função significa ter dependência, ou seja, o valor de f(x) ou y se modifica à medida que modificamos o valor de x. Por isso, as soluções para as funções vêm em pares ordenados (x, y). 

Seguindo a regra matemática podemos desenhar um gráfico para a função e resolver exercícios sobre funções.

• Você é uma daquelas pessoas que tem fome de conhecimento? Então siga o Beduka no Instagram para conteúdos diários. 

Quais os elementos de uma função? 

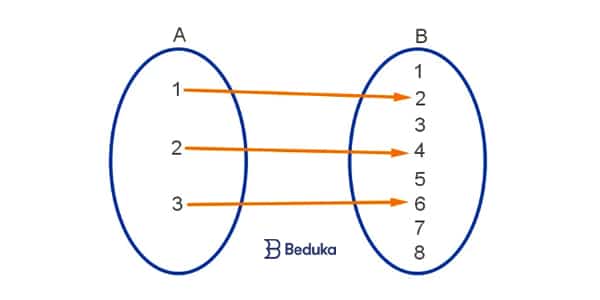
Os elementos de uma função são: 

• Domínio(D)
• Contradomínio(CD)
• Imagem(I) 

Vamos detalhar mais sobre eles: 

Domínio(D)

São todos os valores possíveis de “x”. 

Contradomínio(CD)

São todos os valores possíveis de serem gerados a partir de “x”. 

Imagem(I)

São todos os valores do contradomínio que satisfazem a função (o y de cada x).    

Para que a relação entre conjuntos seja considerada uma função, ela precisa cumprir duas condições: 

1- O domínio deve ser exatamente igual ao conjunto de partida. Isto é, todo elemento do (D) deve ser ponto de partida de uma “flecha”. Se houver um elemento de D do qual não se “parta uma flecha”, não é uma função!

2- Cada elemento de D só pode ter UMA correspondência no conjunto CD. De forma figurada, só pode “partir 1 flecha” de cada elemento do Domínio. Se um valor em D tiver “duas flechas” (ou mais) saindo de si mesmo, não é uma função!

Quais são os tipos de Funções?

Os tipos de funções matemáticas são: 

Função Injetora

Cada elemento do Domínio possui um único elemento na Imagem e vice-versa. Porém, podem existir elementos do Contradomínio que não são Imagem, eles sobram no conjunto. Portanto, a Imagem é diferente do Contradomínio.

Função Sobrejetora

Nesta função, cada elemento do Domínio possui um elemento na Imagem, mas pode acontecer de dois elementos do Domínio possuírem uma mesma imagem. 

O que não pode é um elemento do D possuir 2 imagens. Dessa forma, Imagem e o Contradomínio são iguais, não há sobra.

Função Bijetora

Cada elemento do Domínio possui um único elemento na Imagem e vice-versa, só que não há elementos que sobram. 

Por isso, ela pega um aspecto da Injetora (um elemento da  Imagem só pertence a um elemento do Domínio) e outro aspecto da Sobrejetora (não sobram elementos, imagem é igual ao contradomínio).

Função Constante

Na função Constante, qualquer número que colocar em x sempre resultará no mesmo valor de Y. Por esse motivo, o gráfico (resultados possíveis de cada par ordenado) é uma linha horizontal e reta.

Função de Primeiro Grau

Uma função do primeiro grau é aquela em que a lei de formação pode ser escrita na seguinte maneira: f(x) = ax + b

Além disso, o expoente que há na incógnita vale no máximo 1. Por isso é chamada de primeiro grau! Como consequência disso, seu gráfico é sempre uma reta.

As funções de primeiro grau podem ser chamadas de Afim e apresentam alguns tipos: Identidade ou Linear. 

Função do Segundo Grau (Quadrática)

Uma função do segundo grau é aquela em que a lei de formação pode ser escrita na seguinte maneira: f(x) = ax² + bx + c

Além disso, deve haver ao menos um expoente máximo valendo 2, na incógnita . Por isso é chamada de segundo grau! Como consequência disso, seu gráfico é sempre uma parábola.

Observe que o gráfico é composto por um segmento com duas características: uma crescente e outra decrescente. Observe também que ela pode ou não ser simétrica. Se for, pode ser do tipo par ou ímpar!

Função Exponencial

Uma Função Exponencial é caracterizada pela presença da variável (x) no expoente de uma base numérica, em que a lei de formação pode ser escrita na seguinte maneira: 

f(x) = aˣ

Por esse motivo, o seu gráfico é como um braço de hipérbole.

Função Logarítmica

É toda função que possuir um logaritmo na sua lei de formação, seguindo as condições de existência: 

f(x) = loga x

O Log é tido como operação inversa da exponenciação, da mesma forma, os gráficos também são inversos.

Função Par

A função par é toda aquela que for simétrica em relação ao eixo vertical (y) do plano cartesiano. Ao analisar a linha que se forma interligando os possíveis resultados, vemos que elas são como um reflexo de um espelho.

Função Ímpar

A função ímpar é toda aquela que for simétrica em relação ao eixo horizontal (x) do plano cartesiano. Imagine que é uma folha de papel e você dobra bem no lugar do eixo indicado. Observe que as figuras de cada face se encontrarão!

Função Crescente e Decrescente

• Crescente: Função que ao aumentar o valor de x, gera um valor maior de y.
• Decrescente: Função que ao aumentar o valor de x, reduz o valor de y.

As funções de 1° grau, exponenciais e logarítmicas podem ser de um tipo ou de outro. Já as funções de 2° grau e trigonométricas, apresentam um gráfico que contém segmentos dos dois tipos ao mesmo tempo!

Função Trigonométrica

São funções angulares utilizadas no estudo dos triângulos ou fenômenos periódicos. Sua lei de formação sempre terá algum fator trigonométrico:

f(x) = sen x

f(x) = cos x

f(x) = tg x

• Quer ver os gráficos de cada uma dessas funções? Então leia nosso artigo completo sobre funções matemáticas.

Como calcular funções?

Desde que você saiba a lei de formação, basta substituir os valores dados e encontrar os que faltam. O processo é o mesmo de resolver uma equação normal.  

1º Passo: Substitua os valores

Saiba identificar o que cada incógnita representa na conta, leia o enunciado e substitua na lei de formação. 

2º Passo: Elimine os parênteses e faça as operações prioritárias

Algumas expressões podem estar escritas dentro de símbolos, como os parênteses ( ), os colchetes [ ] e as chaves { }. Eles indicam a ordem: 1° resolvemos o que está dentro dos parênteses, 2° o que está dentro dos colchetes e 3° o que está dentro das chaves. 

Se for impossível continuar resolvendo o que está em 1° lugar de prioridade, pulamos para o próximo passo. Apenas depois disso podemos resolver o que está fora.

Uma vez que identificamos as prioridades, podemos efetuar as operações. Elas também têm uma ordem: 1º potenciação e radiciação; 2º multiplicação e divisão e 3º soma e subtração.

Se existir mais de uma operação com a mesma prioridade, elas serão resolvidas da esquerda para direita.

3º Passo: Transponha os termos

Após isso, para podermos trocar os termos e organizá-los em cada membro, devemos mudar o sinal que ele carregava para o seu oposto:

Aquilo que está negativo passa como positivo e vice-versa. O que está multiplicando passa dividindo e vice-versa. Se havia raiz quadrada, passa como potência de expoente ½ e vice-versa. 

Ao passar as incógnitas de lado, devemos mantê-las juntas aos seus coeficientes e à base em que está. 

4º Passo: Reduza os termos semelhantes 

Depois disso, efetue as operações entre termos semelhantes (número com número e letra com letra). 

5º Passo: Isole a incógnita

Quando não há mais nada a ser feito, aí isolamos a incógnita de um lado e aplicamos as propriedades ou operações para descobrir seu valor.

NOTA: As condições de existência de cada função vão influenciar nas formas de resolver os exercícios sobre funções.

Por exemplo, não tem como resolver uma função exponencial sem usar a potenciação. Da mesma maneira, não tem como resolver uma função logarítmica sem usar logaritmo. 

Exercícios sobre funções com Gabarito

Esperamos que, com esse resumo, tudo tenha ficado mais claro para você. 

Obrigado por ter lido até aqui!

Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.

Questão 1- (Encceja 2018) Uma prestadora de serviços cobra pela visita à residência do cliente e pelo tempo necessário para realizar o serviço na residência.

O valor da visita é R$ 40 e o valor da hora para realização do serviço é R$ 20.

Uma expressão que indica o valor a ser pago (P) em função das horas (h) necessárias à execução do serviço é:

a) P = 40h

b) P = 60h

c) P = 20 + 40h

d) P = 40 + 20h

Questão 2- (Enem 2016) Uma cisterna de 6 000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.

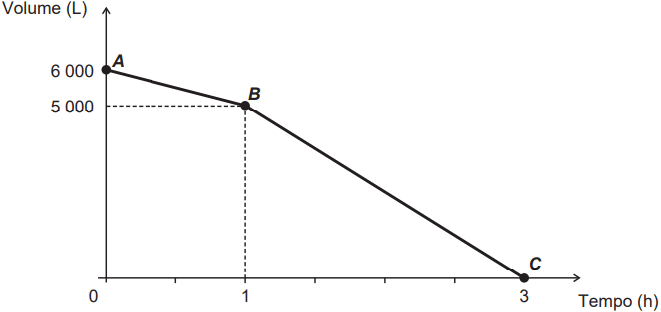
Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?

a) 1 000

b) 1 250

c) 1 500

d) 2 000

e) 2 500

Questão 3- (UFSM) Sabe-se que o preço a ser pago por uma corrida de táxi inclui uma parcela fixa, que é denominada bandeirada, e uma parcela variável, que é função da distância percorrida. Se o preço da bandeirada é de R$ 4,60 e o quilômetro rodado é R$ 0,96, a distância percorrida pelo passageiro que pagou R$ 19 para ir de sua casa ao shopping é de:

a) 5 km

b) 10 km

c) 15 km

d) 20 km

e) 25 km

Questão 4- (UCSal) Sejam f e g funções de R em R, sendo R o conjunto dos números reais, dadas por

f(x) = 2x – 3 e f(g(x)) = -4x + 1. Nestas condições, g(-1) é igual a:

a) -5

b) -4

c) 0

d) 4

e) 5

Questão 5- (UCSal) O maior valor assumido pela função y = 2 – ½ x – 2½ é:

a) 1

b) 2

c) 3

d) 4

e) 5

Questões 6 – (UCSal) O gráfico da função f de R em R, dada por f(x) = ½ 1 – x½ – 2, intercepta o eixo das abcissas nos pontos (a,b) e (c,d). Nestas condições o valor de d + c – b – a é:

a) 4

b) -4

c) 5

d) -5

e) 0

Questão 7-  (UFBA) Se f (g (x) ) = 5x – 2 e f (x) = 5x + 4 , então g(x) é igual a:

a) x – 2

b) x – 6

c) x – 6/5

d) 5x – 2

e) 5x + 2

• Muito bem! Você chegou à metade dos Exercícios sobre funções. Continue fazendo o restante.

Questão 8- (INFO) Chama-se ponto fixo de uma função f a um número x tal que f(x) = x. Se o ponto fixo da função f(x) = mx + 5 é igual a 10, então podemos afirmar que o módulo do décuplo do ponto fixo da função g(x) = 2x – m é igual a:

a) 5

b) 4

c) 3

d) 2

e) 1

Questão 9- (INFO)A diferença entre dois números é 8. O menor valor que se pode obter para o produto é:

a) 16

b) 8

c) 4

d) -4

e) -16

Questão 10- (INFO) Seja f : R ® R , uma função tal que f ( x ) = k.x – 1. Se f [ f ( 2 ) ] = 0 e f é estritamente decrescente, o valor da k-ésima potência de 2 é igual aproximadamente a:

a) 0,500

b) 0,866

c) 0,125

d) 0,366

e) 0,707

Questão 11- (INFO) Seja f(x) = ax + b; se os pares ordenados (1,5) Î f e (2,9) Î f então podemos afirmar que o valor do produto (a + b) (10a + 5b) é igual a:

a) 225

b) 525

c) 255

d) 100

e) 1000

Questão 12- (INFO) A função f é tal que f(2x + 3) = 3x + 2. Nestas condições, f(3x + 2) é igual a:

a) 2x + 3

b) 3x + 2

c) (2x + 3) / 2

d) (9x + 1) /2

e) (9x – 1) / 3

Questão 13- (UA–AM) Após várias experiências em laboratórios, observou-se que a concentração de certo antibiótico, no sangue de cobaias, varia de acordo com a função y = 12x – 2x², em que x é o tempo decorrido, em horas, após a ingestão do antibiótico. Nessas condições, qual o tempo necessário para atingir o nível máximo de concentração desse antibiótico, no sangue dessas cobaias? 

a) 6 horas

b) 3 horas

c) 18 horas

d) 12 horas

e) 9 horas

Questão 14- (FGV-SP) Um capital de R$ 12 000,00 foi aplicado em regime de juros compostos a uma taxa de 2,5% ao mês durante 12 meses. Ao retirar o montante resultante da aplicação a pessoa terá descontado do juro da aplicação 7% de imposto sobre aplicações financeiras envolvendo lucros mais 0,5% de contribuição para obras relacionadas à saúde pública, segurança e educação, totalizando 7,5% de descontos. Calcule o valor líquido dessa aplicação, isto é, o valor debitado os impostos.   

a) R$4138,67

b) R$16.138,67

c) R$ 310,67

d) R$12.000,00

e) R$15.828,27

• Parabéns, você fez todos os Exercícios sobre funções. Confira agora o Gabarito:

Gabarito dos Exercícios sobre funções

Exercício resolvido da questão 1 –

Alternativa correta: d) P = 40 + 20h

Exercício resolvido da questão 2 –

Alternativa correta: c) 1 500

Exercício resolvido da questão 3 –

Alternativa correta: c) 15 km

Exercício resolvido da questão 4 –

Alternativa correta: d) 4

Exercício resolvido da questão 5 –

Alternativa correta: b) 2

Exercício resolvido da questão 6 –

Alternativa correta: a) 4

Exercício resolvido da questão 7 –

Alternativa correta: c) x – 6/5

Exercício resolvido da questão 8 –

Alternativa correta: a) 5

Exercício resolvido da questão 9 –

Alternativa correta: e) -16

Exercício resolvido da questão 10 –

Alternativa correta: e) 0,707

Exercício resolvido da questão 11 –

Alternativa correta: a) 225

Exercício resolvido da questão 12 –

Alternativa correta: d) (9x + 1) /2

Exercício resolvido da questão 13 –

Alternativa correta: b) 3 horas

Exercício resolvido da questão 14 –

Alternativa correta: e) R$15.828,27

Estude para o Enem com o Simulado Beduka. É gratuito!

Gostou dos nossos Exercícios sobre funções? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.