Os planos são uma daquelas coisas que ninguém sabe definir, mas entende o que é! Curioso, não? Leia o resumo para organizar o seu conhecimento e treine seus com os exercícios sobre Planos na Matemática. Ao final, haverá um gabarito para confirmar suas respostas!
Quer seguir diretamente para alguma parte? Clique em um dos tópicos abaixo:
- Definição: o que são Planos na Matemática?
- Quais as Características dos Planos matemáticos?
- Os 10 melhores exercícios sobre Planos na Matemática!
- Gabarito das questões de Planos na Matemática.
Quando você terminar as atividades de Planos na Matemática, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil!
Conceito: o que é um Plano na Matemática?
O Plano é um dos três entes primitivos da geometria (os outros são o Ponto e a Reta). Isso significa que ele é a base dos outros conceitos e representações que estudamos adiante!
De forma bem simples e prática, um plano seria como uma folha de papel em branco. Ou seja: liso, reto, com largura e comprimento. Eles também correspondem aos lados ou faces dos sólidos geométricos.
Na verdade, não existe uma definição objetiva… Mas podemos falar sobre suas origem e características!
- São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
Quais as Características dos Planos matemáticos?
Se o conjunto de pontos formam uma reta, dizemos que o conjunto de retas formam o plano. Pela consequência da definição da reta, podemos dizer que o plano também é um conjunto de pontos, dispostos em uma rede fina e horizontal.
A área formada por esse alinhamento de retas e pontos é uma superfície plana, por isso chamada de Plano!
Ele se estende ao infinito e não possui espessura ou profundidade. Inclusive, ele serve como base para a construção das figuras planas (quadrado, triângulo, círculo, etc.).
Vamos resumir suas características:
- O plano é uma superfície reta, não faz curva.
- O plano é bidimensional (podemos medir sua altura e largura, como uma folha de papel).
- É representado por letras gregas minúsculas, como α, β, etc.
- O plano é infinito.
- É possível desenhar figuras sobre o plano.
- Um plano pode ser formado por 3 pontos não colineares (imagine um triângulo, ele é uma região plana com 3 vértices).
- Também pode ser formado por 1 reta mais um ponto fora dela.
- Um plano pode ser formado por duas retas concorrentes ou paralelas distintas.
- Há posições relativas entre os planos.
- No Plano Cartesiano, vemos as relações entre reta, ponto e plano!
Também temos um artigo sobre o que é Ponto, Reta, Plano e Espaço!
Os 10 exercícios sobre Planos na Matemática!
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Obrigado por ter lido até aqui!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1- (ESFCEX 2009)
Sobre os elementos primitivos da geometria espacial, assinale a alternativa correta.
a) Dois planos paralelos a uma reta são paralelos entre si.
b) Quatro pontos não coplanares determinam quatro planos.
c) Duas retas distintas não paralelas se cortam em um ponto.
d) Três planos distintos sempre se cortam segundo uma reta.
e) Duas retas distintas ortogonais a uma terceira são ortogonais entre si.
Questão 2- (UFAL)
Na cadeira representada na figura a seguir, o encosto é perpendicular ao assento e este é paralelo ao chão.
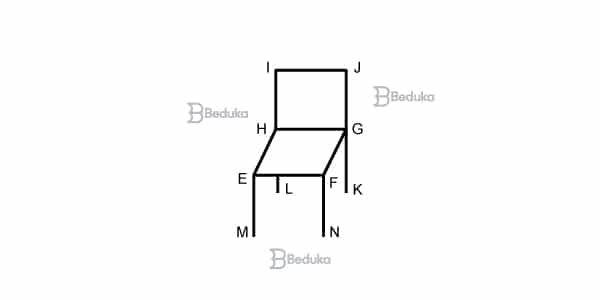
Sendo assim:
a) os planos EFN e FGJ são paralelos.
b) HG é um segmento de reta comum aos planos EFN e EFH.
c) os planos HIJ e EGN são paralelos.
d) EF é um segmento de reta comum aos planos EFN e EHG.
- Você já fez 20% dos exercícios de Planos na Matemática. Continue assim!
Questão 3- (Stoodi)
A Geometria Plana na Matemática é composta por um conjunto de retas, pontos e planos os quais dão origem a infinitas figuras e desenhos geométricos.
Considerando as definições dos elementos que compõem a Geometria Plana, é falso afirmar que:
a) um ponto não pode ser atravessado por mais que uma reta.
b) é impossível determinar o comprimento de uma reta, já que ela é adimensional.
c) um plano pode ser criado a partir de duas retas paralelas.
d) todos os pontos são especificados na Matemática como algo adimensional.
Questão 4- (Fatec -SP)
Seja A um ponto pertencente à reta r, contida no plano α. É verdade que:
a) existe uma única reta que é perpendicular à reta r no ponto A.
b) existe uma única reta, não contida no plano α, que é paralela à reta r.
c) existem infinitos planos distintos entre si, paralelos ao plano α, que contém a reta r.
d) existem infinitos planos distintos entre si, perpendiculares ao plano α e que contêm a reta r.
e) existem infinitas retas distintas entre si, contidas no plano α e que são paralelas à reta r.
Questão 5- (Brasil Escola)
Assinale a alternativa correta a respeito dos planos em Geometria.
a) Um plano é uma figura formada por retas, mas não por pontos.
b) Existem pelo menos um ponto em um plano e um ponto fora dele.
c) É possível construir um plano com apenas duas retas. Para isso, basta que elas sejam coincidentes.
d) Para que uma reta seja perpendicular a um plano, basta que ela seja perpendicular a uma reta que pertença a ele.
e) Para que dois planos sejam secantes, basta que possuam um ponto em comum.
- Nossa! Você já fez metade das questões sobre Planos na Matemática. Vamos lá!
Questão 6- (PM RJ – Exatus 2014)
Sobre retas, planos e suas relações posicionais, Adriana escreveu em seu caderno as seguintes afirmações:
I – Se duas retas distintas são paralelas a um plano, então elas são paralelas entre si.
II – Se uma reta r está contida em um plano α , então existem retas paralelas a r fora de α .
III – Duas retas concorrentes podem ser ortogonais.
IV – Dada uma reta r paralela a um plano α , então r não é paralela a todas as retas de α .
Está correto apenas o que se afirma em:
a) Apenas as afirmativas I e II.
b) Apenas as afirmativas II e III.
c) Apenas as afirmativas II e IV.
d) Apenas as afirmativas III e IV.
Questão 7- (Brasil Escola)
A respeito das posições relativas entre reta e plano, assinale a alternativa correta:
a) Dadas duas retas coincidentes r e s. Se a reta r estiver contida em um plano qualquer, não poderemos garantir que a reta s também estará contida nesse mesmo plano.
b) Dada a reta r e o ponto A, fora da reta r. Pelo ponto A, sabemos que existe uma reta s que contém o ponto A tal que r é paralela a s.
c) Uma reta está contida em um plano quando possui apenas dois pontos em comum com ele. Nenhum ponto a mais, nenhum ponto a menos.
d) Uma reta está contida em um plano quando possui apenas um ponto em comum com ele.
e) Uma reta está contida em um plano quando essas duas figuras não possuem pontos em comum.
Questão 8- (Matematiquês)
Considerando a figura abaixo, onde a reta r é perpendicular ao plano α e s é uma reta desse mesmo plano, assinale o que for correto:
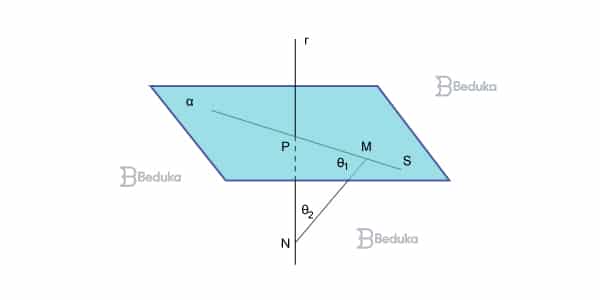
1- r e s são perpendiculares.
2- r e s determinam um plano perpendicular a α.
4- O triângulo PMN é equilátero.
8- r pertence a α.
16- A soma dos ângulos θ1 e θ2 é 90°.
- Ufa! Agora só faltam mais dois exercícios de Planos na Matemática!
Questão 9- (Brasil Escola)
A respeito das posições relativas entre retas e planos, assinale a alternativa correta:
a) Duas retas distintas, r e s, são paralelas. Se a reta r está contida no plano A, e a reta s está contida no plano B, então A e B jamais podem encontrar-se.
b) Duas retas r e s são reversas. Se a reta r está contida no plano A, então a reta s não está contida nesse mesmo plano.
c) Por um ponto fora de um plano, passa uma única reta paralela a esse plano dado.
d) Uma reta r é paralela a um plano somente se existirem duas retas contidas nesse plano e perpendiculares à reta r.
e) Uma reta é paralela a um plano quando possui dois pontos em comum com ele.
Questão 10 – (Matematiquês-adaptada)
Leia as afirmativas abaixo e escolha a alternativa correta:
I. Dados um plano α e dois pontos A e B fora dele é sempre possível passar por A e B um plano perpendicular a α.
II. Dadas 2 retas reversas a e b não existe nenhum plano eqüidistante das duas retas.
III. Se a intersecção de duas retas é o conjunto vazio, elas são paralelas ou reversas.
IV. Quatro pontos distintos e não-coplanares determinam exatamente 5 planos.
V. Se dois planos forem perpendiculares, todo plano perpendicular a um deles será perpendicular ao outro.
São verdadeiras:
a) I e III.
b) I e II.
c) III e IV.
d) IV e V.
e) II e V.
- Parabéns, você fez todas as atividades sobre Planos na Matemática. Confira agora o Gabarito:
Gabarito dos exercícios sobre Planos na Matemática
Exercício resolvido da questão 1 –
Alternativa correta: c) Duas retas distintas não paralelas se cortam em um ponto.
Exercício resolvido da questão 2 –
Alternativa correta: d) EF é um segmento de reta comum aos planos EFN e EHG.
Exercício resolvido da questão 3 –
Alternativa correta: a) um ponto não pode ser atravessado por mais que uma reta.
Exercício resolvido da questão 4 –
Alternativa correta: e) existem infinitas retas distintas entre si, contidas no plano α e que são paralelas à reta r.
Exercício resolvido da questão 5 –
Alternativa correta: b) Existem pelo menos um ponto em um plano e um ponto fora dele.
Exercício resolvido da questão 6 –
Alternativa correta: c) Apenas as afirmativas II e IV.
Exercício resolvido da questão 7 –
Alternativa correta: b) Dada a reta r e o ponto A, fora da reta r. Pelo ponto A, sabemos que existe uma reta s que contém o ponto A tal que r é paralela a s.
Exercício resolvido da questão 8 –
Alternativa correta: 1, 2 e 16.
Exercício resolvido da questão 9 –
Alternativa correta: b) Duas retas r e s são reversas. Se a reta r está contida no plano A, então a reta s não está contida nesse mesmo plano.
Exercício resolvido da questão 10 –
Alternativa correta: a) I e III.
- Estude para o Enem com o Simulado Enem do Beduka. É gratuito!
Gostou dos nossos exercícios sobre Planos na Matemática? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.





