Na matemática, os Planos são um daqueles elementos que quase ninguém sabe explicar, mas que usamos o tempo todo! Para dominar mesmo a Geometria Plana e a Espacial, é preciso entender quais são as suas características, seus tipos, ver exemplos aplicados e conhecer os intrigantes postulados!
Neste resumo sobre os planos na matemática, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:
- Introdução: o que é a Geometria?
- O que é o Plano na matemática?
- Como um Plano pode ser definido?
- O que são os Postulados ou Axiomas do Plano?
- Qual a diferença entre Plano e Espaço?
- Quais são as posições relativas entre Planos?
- Resumo: características dos Planos.
Depois você pode testar o que aprendeu. É só fazer o nosso Simulado ENEM gratuito! Ele pode ser personalizado com as matérias que você quiser.
Introdução: o que é a Geometria?
Antes de tudo, é preciso saber que o plano é um elemento da Geometria. Isso significa que estamos lidando com uma parte da matemática que se baseia nas representações gráficas (desenhos).
O conceito de plano surge na Geometria Plana. Depois, eles são muito usados para construir a Geometria Espacial, embora não citamos diretamente o seu nome.
Nós só estamos querendo te mostrar que esse é um elemento muito importante. Mas fique tranquilo, nos próximos tópicos, explicaremos os conceitos em cada área e daremos exemplos!
- São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
O que é um plano na matemática?
O Plano é um dos três entes primitivos da geometria. Isso significa que ele é a base dos outros conceitos e representações que estudamos adiante. Os outros entes são o Ponto e Reta, que precisamos conhecer antes de avançarmos!
De forma bem simples e prática, um plano seria como uma folha de papel em branco. Ou seja: liso, reto, com largura e comprimento. Mas não é só isso não…
Agora que já temos uma ideia de partida, podemos entender as definições matemáticas e a sua utilidade:
Como um plano pode ser definido matematicamente?
Assim como o ponto e a reta, não existe uma definição objetiva… Por isso é tão difícil para os professores explicarem e os alunos entenderem! Mas podemos falar sobre suas origem e características.
Se o conjunto de pontos formam uma reta, dizemos que o conjunto de retas formam o plano. Assim, o plano é um conjunto de retas alinhadas, coladinhas umas nas outras.
Pela consequência da definição da reta, podemos dizer que o plano também é um conjunto de pontos, dispostos em uma rede fina e horizontal. A área formada por esse alinhamento de retas e pontos é uma superfície plana, por isso chamada de Plano!
Ele se estende ao infinito e não possui espessura ou profundidade. Inclusive, ele serve como base para a construção das figuras planas (quadrado, triângulo, círculo, etc.).
Até agora pode ser que você tenha lido só coisas óbvias, então vamos dar um passo adentro:
Como representamos um plano na matemática?
Os planos são nomeados por alguma letra minúscula do alfabeto grego (α, β); bem como os pontos são representados por letras maiúsculas do alfabeto latino e as retas por pelas minúsculas.
Além disso, representamos os planos como uma região plana, exatamente como uma folha ou superfície reta em que podemos desenhar coisas.
- Porém, o mais intrigante sobre os planos são os seus postulados:
O que são os Postulados sobre o Plano?
Os Postulados, também chamados de axiomas, são frases que descrevem uma certeza. Elas não precisam de uma razão ou demonstração, define-se que aquilo existe e a partir daí se constrói tudo o mais.
Já que os entes primitivos não podem ser definidos, apenas descrevemos suas características. É de se esperar que as suas existências sejam garantidas pelos postulados.
No caso específico do plano, o postulado de sua existência é:
“Existem planos e, neles ou fora deles, existem pontos.”
Há, também, o postulado da inclusão:
“Se um plano contém dois pontos distintos de uma reta, ele contém toda essa reta.”
Há outros dois postulados que indicam o que acontece quando traçamos uma reta em um plano, ou um plano em um espaço. Eles seguem o mesmo raciocínio, veja:
“Uma reta divide um plano em duas partes nas quais ela está contida.”
“Um plano divide o espaço em duas partes nas quais ele está contido.”
Postulados da origem do Plano
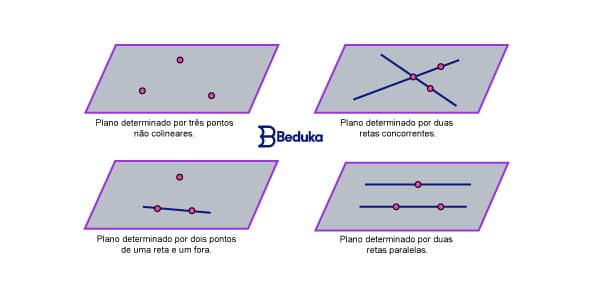
Além desses axiomas que já vimos, também existem postulados de determinação. Esses são conceitos que falam sobre como podemos identificar que ali se formou um plano.
Eles falam sobre as possibilidades de formação de um plano:
“Três pontos não colineares determinam um plano único que os contém.”
“Dois pontos distintos na reta e o ponto fora dela também determinam um plano.”
“Duas retas concorrentes encontram-se em um ponto. Tome outros dois pontos, um em cada reta. Esses dois últimos e o primeiro não são colineares, logo, determinam um plano.”
“Sejam duas retas paralelas, tome dois pontos de uma delas e um ponto na outra. Esse último e os dois primeiros não são colineares, logo, determinam um plano.”
Qual a diferença entre Plano e Espaço?
Agora que já entendemos o que é um plano, podemos dizer que cada face de um sólido geométrico está em um plano.
E adivinhe só? Os sólidos são figuras da Geometria Espacial.
Isso já nos dá uma dica: o espaço é o conjunto de vários planos, de modo que não haja nenhuma distância entre eles. O espaço é tudo o que está ao redor, é como o universo.
Sendo assim, podemos associar que: cada vértice é um ponto, cada aresta é uma reta, cada face é um plano e o espaço é onde todos esses elementos se encontram!
Quais são as posições relativas entre planos?
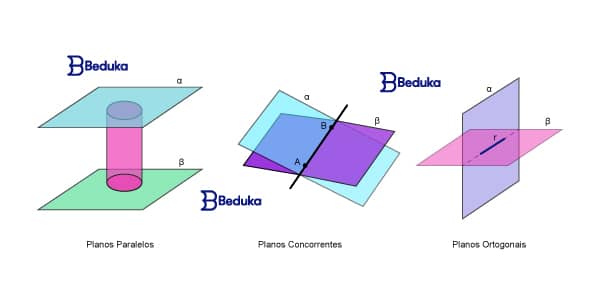
Nós só lidamos com um único plano na Geometria Plana, mas na Espacial veremos vários ao mesmo tempo. Assim, é possível classificar os planos dependendo da posição que eles têm entre si.
- Paralelos ou deformes: Não possuem nenhum ponto em comum. Ex: os planos das bases dos cilindros.
- Secantes ou Concorrentes: possuem pontos em comum, formando uma reta na interseção.
- Ortogonais ou Perpendiculares: são planos secantes que formam ângulos especificamente de 90°.
Resumo: como podemos caracterizar os planos?
- O plano é uma superfície reta, não faz curva.
- O plano é bidimensional (podemos medir sua altura e largura, como uma folha de papel).
- É representado por letras gregas minúsculas, como α, β, etc.
- O plano é infinito.
- É possível desenhar figuras sobre o plano.
- Um plano pode ser formado por 3 pontos não colineares (imagine um triângulo, ele é uma região plana com 3 vértices).
- Também pode ser formado por 1 reta mais um ponto fora dela.
- Um plano pode ser formado por duas retas concorrentes ou paralelas distintas.
- Há posições relativas entre os planos.
Alguns matemáticos, como Descartes, fizeram um plano com elementos destacados. Estamos falando daquele que tem 2 retas em sentidos diferentes e alguns de seus pontos são representados por números.
É isso mesmo, estamos falando do Plano Cartesiano! É essencial saber seus elementos e como usá-lo, não deixe de ler o artigo!
Gostou do nosso resumo sobre os planos na matemática? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





