A probabilidade é um conceito na matemática que calcula possibilidade de um certo evento ocorrer . É através dela, por exemplo, que podemos descobrir a chance de obter cara ou coroa no lançamento de uma moeda.
Leia abaixo o nosso resumo para relembrar e treine com os melhores exercícios de probabilidade. Tem gabarito!
Neste artigo, você encontrará todos os temas abaixo. Clique em um dos tópicos abaixo para ir direto ao conteúdo da sua escolha:
- Definições básicas de probabilidade.
- Como calcular Probabilidade?
- Lista de exercícios de Probabilidade.
- Gabarito dos exercícios sobre Probabilidade!
Quando você terminar as questões sobre Probabilidade, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil.
Domine os temas mais exigidos de matemática no Enem e conquiste uma boa nota.
Supere os desafios do Enem!
Definições básicas de probabilidade
Com esses conceitos iniciais será mais fácil responder à cada uma das questões de vestibulares que selecionamos para você treinar.
O que é experimento aleatório?
São acontecimentos que, quando repetidos inúmeras vezes em processos semelhantes, possuem alta diversidade de resultados, isto é, o mesmo fenômeno pode ter várias soluções diferentes.
Ao lançar um dado, por exemplo, podemos obter um total de 6 resultados aleatórios. Essas alternâncias de resultados dentro de um mesmo fenômeno são particularidades dos experimentos aleatórios.
Espaço amostral
Espaço amostral de um experimento aleatório é o conjunto de todos os resultados possíveis do experimento.
Exemplo:
No caso do lançamento de um dado, o espaço amostral, geralmente indicado pela letra S, seria:
S= {1,2,3,4,5,6}
Evento
Na probabilidade, evento é qualquer subconjunto de um espaço amostral. Ele pode conter nenhum elemento ou todos os elementos do espaço amostral.
Exemplo:
Sair um número par no lançamento de um dado.
O evento é sair um número par:
E = {2, 4, 6}
O seu número de elementos do evento é 3.
- São mais de 200 resumos no Instagram do Beduka!
Como calcular probabilidade?
Se, em um experimento aleatório, as várias possibilidades de resultados têm chances iguais de ocorrer, a probabilidade de um certo evento A é medida pela divisão entre o número de eventos favoráveis e o número total de resultados possíveis.
A probabilidade é determinada pela seguinte fórmula:
P(A) = nª/n
Onde nª é o número de eventos favoráveis e n ao número de casos possíveis.
Voltando ao exemplo do dado ao ser lançado.
São 3 formas diferentes do número par sair dentro das 6 possibilidades existentes que são todas iguais. Nesse contexto, concluímos que:
P(A) = 3/6
(3 possibilidades e sair o número par entre 6 resultados totais possíveis)
P(A)= 1/2
P(A)= 50%
Calculando exercícios de probabilidade de múltiplos eventos aleatórios
Para calcular a probabilidade de eventos múltiplos em um espaço amostral devemos dividir o problema em probabilidades separadas.
Tomando o exemplo do lançamento do dado novamente, vamos considerar as probabilidades de obter dois “cincos” consecutivos com o dado de seis lados:
- A probabilidade de sair um cinco é igual a 1/6.
- A probabilidade de obtermos outro cinco também é igual a 1/6.
Esses são eventos independentes, porque o resultado obtido no primeiro lançamento não influencia o do segundo.
Multiplicando as probabilidades de ambos os evento, teremos o resultado da probabilidade de múltiplos eventos acontecendo um após o outro. Temos então:
P(A)= 1/6 × 1/6
P(A)= 1/36
P(A)= 0,027 ou 2,7%.
Exercícios de probabilidade com gabarito
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Parabéns por ter lido até aqui!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1 – (UFV-04)
Os bilhetes de uma rifa são numerados de 1 a 100. A probabilidade do bilhete sorteado ser um número maior que 40 ou número par é:
a) 60%.
b) 70%.
c) 80%.
d) 90%.
e) 50%.
Questão 2 –
Os números naturais de 1 a 10 foram escritos, um a um, sem repetição, em dez bolas de pingue-pongue. Se duas delas forem escolhidas ao acaso, o valor mais provável da soma dos números sorteados é igual a:
a) 9.
b) 10.
c) 11.
d) 12.
e) 13.
Questão 3 –
Uma moeda é viciada, de forma que as caras são três vezes mais prováveis de aparecer do que as coroas. Determine a probabilidade de num lançamento sair coroa.
a) 25%.
b) 50%.
c) 35%.
d) 70%.
e) 20%.
Questão 4 –
Um cartão é retirado aleatoriamente de um conjunto de 50 cartões numerados de 1 a 50. Determine a probabilidade do cartão retirado ser de um número primo.
a) ⅓.
b) ⅕.
c) ⅖.
d) 3/10.
e) 7/10.
- Você já fez 20% das questões sobre Probabilidade. Continue assim!
Questão 5 –
Escolhem-se ao acaso dois números naturais distintos, de 1 a 20. Qual a probabilidade de que o produto dos números escolhidos seja ímpar?
a) 9/38.
b) ½.
c) 9/20.
d) ¼.
e) 8/25.
Questão 6 –
Uma carta é retirada de um baralho comum, de 52 cartas, e, sem saber qual é a carta, é misturada com as cartas de um outro baralho idêntico ao primeiro. Retirando, em seguida, uma carta do segundo baralho, a probabilidade de se obter uma dama é:
a) 3/51.
b) 5/53.
c) 5/676.
d) 1/13.
e) 5/689.
Questão 7 –
Três pessoas A, B e C vão participar de um concurso num programa de televisão. O apresentador faz um sorteio entre A e B e, em seguida, faz um sorteio, para decidir quem iniciará o concurso. Se em cada sorteio as duas pessoas têm a mesma “chance” de ganhar, qual é a probabilidade de A iniciar o concurso?
a) 12,5%.
b) 25%.
c) 50%.
d) 75%.
e) 95%.
Questão 8 – (Enem/2012)
O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa.
O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido. Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta.
As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.
O diretor sabe que algum aluno acertará a resposta porque há:
a) 10 alunos a mais do que possíveis respostas distintas.
b) 20 alunos a mais do que possíveis respostas distintas.
c) 119 alunos a mais do que possíveis respostas distintas.
d) 260 alunos a mais do que possíveis respostas distintas.
e) 270 alunos a mais do que possíveis respostas distintas.
Questão 9 – (Enem/2012)
Em um jogo há duas urnas com dez bolas de mesmo tamanho em cada urna. A tabela a seguir indica as quantidades de bolas de cada cor em cada urna.

Uma jogada consiste em:
- 1.º: o jogador apresenta um palpite sobre a cor da bola que será retirada por ele da urna 2
- 2.º: ele retira, aleatoriamente, uma bola da urna 1 e a coloca na urna 2, misturando-a com as que lá estão
- 3.º: em seguida ele retira, também aleatoriamente, uma bola da urna 2
- 4.º: se a cor da última bola retirada for a mesma do palpite inicial, ele ganha o jogo
Qual cor deve ser escolhida pelo jogador para que ele tenha a maior probabilidade de ganhar?
a) Azul.
b) Amarela.
c) Branca.
d) Verde.
e) Vermelha.
Questão 10 – (Enem/2013)
Numa escola com 1.200 alunos foi realizada uma pesquisa sobre o conhecimento desses em duas línguas estrangeiras: inglês e espanhol.
Nessa pesquisa constatou-se que 600 alunos falam inglês, 500 falam espanhol e 300 não falam qualquer um desses idiomas.
Escolhendo-se um aluno dessa escola ao acaso e sabendo-se que ele não fala inglês, qual a probabilidade de que esse aluno fale espanhol?
a) ½.
b) ⅝.
c) ¼.
d) ⅚.
e) 5/14.
- Muito bem! Você está na metade das questões de Probabilidade!
Questão 11 – (Enem/2013)
Considere o seguinte jogo de apostas:
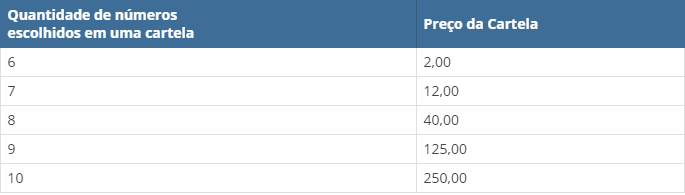
Numa cartela com 60 números disponíveis, um apostador escolhe de 6 a 10 números. Dentre os números disponíveis, serão sorteados apenas 6.
O apostador será premiado caso os 6 números sorteados estejam entre os números escolhidos por ele numa mesma cartela.
O quadro apresenta o preço de cada cartela, de acordo com a quantidade de números escolhidos.
Cinco apostadores, cada um com R$ 500,00 para apostar, fizeram as seguintes opções:
- Arthur: 250 cartelas com 6 números escolhidos
- Bruno: 41 cartelas com 7 números escolhidos e 4 cartelas com 6 números escolhidos
- Caio: 12 cartelas com 8 números escolhidos e 10 cartelas com 6 números escolhidos
- Douglas: 4 cartelas com 9 números escolhidos
- Eduardo: 2 cartelas com 10 números escolhidos
Os dois apostadores com maiores probabilidades de serem premiados são:
a) Caio e Eduardo.
b) Arthur e Eduardo.
c) Bruno e Caio.
d) Arthur e Bruno.
e) Douglas e Eduardo.
Questão 12 – (PUC-RIO 2010)
Quatro moedas são lançadas simultaneamente. Qual é a probabilidade de ocorrer coroa em uma só moeda?
a) ⅛.
b) 2/9.
c) ¼.
d) ⅓.
e) ⅜.
Questão 13 – (PUC-RIO 2009)
Jogamos dois dados comuns. Qual a probabilidade de que o total de pontos seja igual a 10?
a) 1/12.
b) 1/11.
c) 1/10.
d) 2/23.
e) ⅙.
Questão 14 – (PUC-RIO 2008)
No jogo de Lipa sorteia-se um número entre 1 e 600 (cada número possui a mesma probabilidade). A regra do jogo é: se o número sorteado for múltiplo de 6 então o jogador ganha uma bola branca e se o número sorteado for múltiplo de 10 então o jogador ganha uma bola preta. Qual a probabilidade de o jogador não ganhar nenhuma bola?
a) 13/17.
b) 11/15.
c) 23/30.
d) ⅔.
e) ½.
Questão 15 – (PUC-RIO 2008)
A probabilidade de um casal com quatro filhos ter dois do sexo masculino e dois do sexo feminino é:
a) 60%.
b) 50%.
c) 45%.
d) 37,5%.
e) 25%.
Questão 16 – (PUC – RIO 2007)
A probabilidade de um dos cem números 1, 2, 3, 4, …, 100 ser múltiplo de 6 e de 10 ao mesmo tempo é:
a) 3%.
b) 6%.
c) 2%.
d) 10%.
e) 60%.
- Ufa, estamos quase lá! Faça os quatro últimos exercícios sobre Probabilidade!
Questão 17 – (UFMG 2009)
Dois jovens partiram, do acampamento em que estavam, em direção à Cachoeira Grande e à Cachoeira Pequena, localizadas na região, seguindo a trilha indicada neste esquema:
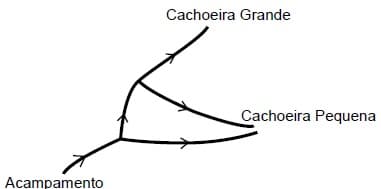
Em cada bifurcação encontrada na trilha, eles escolhiam, com igual probabilidade, qualquer um dos caminhos e seguiam adiante. Então, é CORRETO afirmar que a probabilidade de eles chegarem à Cachoeira Pequena é:
a) ½.
b) ⅔.
c) ¾.
d) ⅚.
Questão 18 – (UFMG 2008)
Considere uma prova de Matemática constituída de quatro questões de múltipla escolha, com quatro alternativas cada uma, das quais apenas uma é correta. Um candidato decide fazer essa prova escolhendo, aleatoriamente, uma alternativa em cada questão. Então, é CORRETO afirmar que a probabilidade de esse candidato acertar, nessa prova, exatamente uma questão é:
a) 27/64.
b) 27/256.
c) 9/64.
d) 9/256.
Questão 19 – (Fuvest 2009)
Dois dados cúbicos, não viciados, com faces numeradas de 1 a 6, serão lançados simultaneamente. A probabilidade de que sejam sorteados dois números consecutivos, cuja soma seja um número primo, é de:
a) 2/9.
b) ⅓.
c) 4/9.
d) 5/9.
e) ⅔.
Questão 20 – (ADVISE 2009)
O quadro funcional de uma empresa é composto de 35 pessoas efetivas e 15 pessoas prestadoras de serviços. Do pessoal efetivo 20 são homens e do pessoal prestador de serviço 5 são mulheres. Escolhendo aleatoriamente uma pessoa dessa empresa, a probabilidade dessa pessoa ser homem ou prestar serviço é:
a) ⅕.
b) 7/10.
c) 9/10.
d) ⅗.
e) ⅘.
- Parabéns, você fez todos os exercícios de probabilidade!
Gabarito dos exercícios sobre probabilidade
Exercício resolvido da questão 1
Alternativa correta: c) 80%.
Exercício resolvido da questão 2
Alternativa correta: c) 11.
Exercício resolvido da questão 3
Alternativa correta: a) 25%.
Exercício resolvido da questão 4
Alternativa correta: d) 3/10.
Exercício resolvido da questão 5
Alternativa correta: a) 9/38.
Exercício resolvido da questão 6
Alternativa correta: d) 1/13.
Exercício resolvido da questão 7
Alternativa correta: b) 25%.
Exercício resolvido da questão 8
Alternativa correta: a) 10 alunos a mais do que possíveis respostas distintas.
Exercício resolvido da questão 9
Alternativa correta: e) Vermelha.
Exercício resolvido da questão 10
Alternativa correta: a) 1/2.
Exercício resolvido da questão 11
Alternativa correta: a) Caio e Eduardo.
Exercício resolvido da questão 12
Alternativa correta: c) 1/4.
Exercício resolvido da questão 13
Alternativa correta: a) 1/12.
Exercício resolvido da questão 14
Alternativa correta: c) 23/30.
Exercício resolvido da questão 15
Alternativa correta: d) 37,5%.
Exercício resolvido da questão 16
Alternativa correta: a) 3%.
Exercício resolvido da questão 17
Alternativa correta: c) 3/4.
Exercício resolvido da questão 18
Alternativa correta: a) 27/64.
Exercício resolvido da questão 19
Alternativa correta: a) 2/9.
Exercício resolvido da questão 20
Alternativa correta: b) 7/10.
Gostou dos nossos exercícios de probabilidade? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, mensalidade e muito mais.
Experimente agora!






12 Comentários
Bom dia!!
Poderia por gentileza rever o gabarito da questão 01. Nas minhas contas a resposta correta seria 90%. No Gabarito consta 80%.
Grata, abraços!!
Boa tarde Viviane! Conferimos aqui e o gabarito é letra D) 80% mesmo.
Por que? Porque a questão pede a possibilidade de ser maior que 40 ou par.
Se há rifas de 0 a 100, então há 60 delas que são maiores que 40. Portanto, 60/100 ou 3/5.
Se queremos saber as pares é só fazer metade 50/100 ou 1/2.
Só que, dentro desses 60 números maiores que 40, eu já estou contando os pares. Para não contá-los repetidamente, precisamos subtraí-los. 60-30 = 30 , representando então 30/100 ou 3/10.
Sendo assim, a condição “ou” indica uma soma e faremos: 3/5 + 1/2 – 3/10 = 0,8 ou 80%.
Olá! gostaria de entender a questão 5.
Veja Manina, entre 1 e 20, temos exatamente 10 números pares e 10 números ímpares. Considerando que uma multiplicação só pode resultar em um número ímpar se os dois números multiplicados forem ímpares, só chegaremos ao resultado se escolhermos dois números ímpares entre os 20 disponíveis. Sendo assim, escolhemos um deles dentre os 10 que existem, e depois escolhemos o segundo entre os 9 que sobraram após a primeira escolha. Apenas assim o resultado dará ímpar.
Como o problema pede a probabilidade, temos que multiplicar a fração que representa a probabilidade de escolheremos um ímpar na primeira opção (10/20) e depois multiplicar essa fração pela que representa a probabilidade de escolhermos um ímpar novamente (9/19). Assim, chegamos 9/38.
boa tarde, eu achei muito INTERESSANTE o site de vocês para estudos! porém deveria ter uma explicação do pq tal conta da o resultado x, pois tem questão que eu não faço a mínima ideia da resolução da conta.
Obrigado pela sugestão, Débora. Vamos trabalhar nisso.
Gostaria de entender a questão 2 de probabilidade
Janderson, o que você deve fazer nessa questão é ver qual o número entre as alternativas que mais pode aparecer como resultado de somas de pares de bolinhas. Por exemplo, quantos pares de bolinhas podem resultar no número 9?
concordo, so as respostas sem os desenvolvimentos, não ajudam .
Um futuro projeto envolve incluir as resoluções nos exercícios, Ricardo. Obrigado pelo apontamento.
boa noite , eu queria perguntar se a resposta da questão 2 está mesmo correta, pois eu fiz a conta e deu outra resposta
Sim, Lucas, o resultado é 11 mesmo, como indicado no gabarito. A questão quer que você diga qual das opções tem mais chance de ser a soma dos números escritos nas bolinhas, quando duas são tiradas ao acaso. As chances do número 11 são as maiores, pois ele pode ser o resultado de 5 somas.