Os 5 melhores exercícios de Produtos Notáveis

Os Produtos notáveis são parte daquela matéria que todo mundo decora pra passar de ano e não aprende nada! Mas é essencial entender esse assunto de verdade, porque ele nos acompanha em outras matérias. Leia o resumo e treine com os exercícios de produtos notáveis.

Neste artigo, você encontrará todos os temas abaixo. Clique em um dos tópicos para ir direto ao conteúdo da sua escolha:

• O que são Produtos Notáveis?
• Quais são os 5 produtos notáveis que caem nas provas?
• Lista de exercícios de Produtos Notáveis!
• Resposta dos exercícios sobre Produtos Notáveis.

Quando você terminar as questões de Produtos Notáveis, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil.

O que são Produtos Notáveis?

Os produtos notáveis são multiplicações que fazemos com polinômios e que o resultado é cheio de propriedades. Assim, podemos fatorar e transformá-los de acordo com algumas regrinhas para cada situação.

Ah, você esqueceu o que é polinômio? são expressões algébricas com duas ou mais letras. Exemplo: 2x+4y. 

• Simples né? Há mais de 200 resumos como esse no Instagram do Beduka!

Quais são os principais casos de Produto Notável?

Existem cinco produtos notáveis que usamos muito durante a vida escolar:

• Quadrado da soma;
• Quadrado da diferença; 
• Produto da soma pela diferença; 
• Cubo da soma;
• Cubo da diferença.

Agora vamos entender sobre o que fazer em cada um deles:

1. Quadrado da soma

O quadrado de um soma é o produto notável que está elevado ao quadrado. (lembre-se que a potência é como uma “evolução” da multiplicação).

Ele é representado pela expressão (x + a)² . Observe que ela possui dois termos quaisquer: o primeiro é “x” e o segundo é “a”. Note que a potência ao quadrado é a multiplicação de um número por ele mesmo. Assim: 3 x 3 = 3².

Portanto, se pegarmos o polinômio x+a e o multiplicarmos por ele mesmo, teremos que o quadrado da soma também pode ser escrito dessa forma: (x + a)(x + a).

Agora você já sabe! Apareça de um jeito ou de outro, temos certeza de que está se referindo ao caso do quadrado da soma. Mas o que fazer diante disso?

Para resolver, basta multiplicar termo por termo. Porém, é muito trabalhoso e desgastante ficar fazendo isso toda hora. Então o ideal é que o aluno decore o padrão.

O resultado do produto notável apresentado sempre será x² + 2xa + a². Nós lemos assim “o quadrado do primeiro termo, mais duas vezes o primeiro e o segundo termo, mais o quadrado do segundo termo”.

Exemplo

Pergunta: Se (x + a)² = x² + 2xa + a², então quanto vale (x + 3)²?

Resposta: x² + 6x + 9

Viu como é importante? Transformamos uma expressão aleatória em uma equação do segundo grau. Então já sabemos o que fazer a partir daqui e achar o valor de x!

2. Quadrado da diferença

O raciocínio que temos aqui é idêntico ao que já falamos aí atrás. A diferença é que temos uma troca de sinal do positivo para o negativo.

Então, a fórmula do quadrado da diferença é (x – a)(x – a) ou (x – a)². Já o seu resultado será semelhante ao da soma, só que troca o primeiro sinal. Será: x² – 2xa + a².

Então ele pode ser lido assim: “o quadrado do primeiro termo, menos duas vezes o primeiro e o segundo termo, mais o quadrado do segundo termo”.

Exemplo

Pergunta: Se (x – a)² = x² – 2xa + a², então quanto vale (4 – y)²?

Resposta: 16 – 8y + y²

Novamente, transformamos uma expressão aleatória em uma equação do segundo grau. Então já sabemos o que fazer a partir daqui e achar o valor de x!

3. Produto da soma pela diferença

O produto da soma pela diferença relaciona uma soma e uma outra subtração. Assim: (x + a)(x – a). Como cada um dos sinais estão diferentes, não conseguimos representar em uma potência única.

Então já vamos te contar logo qual será o resultado: x² – a².

Lemos assim: ” O quadrado do primeiro termo menos o quadrado do segundo termo”.

Exemplo

Pergunta: Se (x + a)(x – a) = x² – a², então quanto vale (z + 2)(z – 2)?

Resposta: z² + 4

Agora chegamos à forma simplificada desse polinômio. Muitas vezes não dará para encontrar um valor numérico para a incógnita, então a resposta terá apenas o polinômio reduzido mesmo.

4. Cubo da soma

Lembra que a gente falou do quadrado da soma? Então, o cubo da soma segue uma lógica parecida, só que ao invés de elevar a dois, estamos elevando a três (cubo).

Por isso, um polinômio escrito dessa forma: (x + a)(x + a)(x + a) pode aparecer também assim: (x + a)³.

Como de costume, o resultado será: x³ + 3x²a + 3xa² + a³. Podemos lê-lo assim: “o cubo do primeiro termo, mais três vezes o quadrado do primeiro pelo segundo termo, mais três vezes o primeiro termo pelo quadrado do segundo, mais o cubo do segundo termo.”

Exemplo

Pergunta: Se (x + a)³ = x³ + 3x²a + 3xa² + a³, então quanto vale (b + 5)³?

Resposta: b³ + 15b² + 75b + 125

5. Cubo da diferença

Por último mas não menos importante, temos o cubo da diferença. O raciocínio que temos aqui é idêntico ao tópico anterior. Novamente, a diferença é que temos uma troca de sinal do positivo para o negativo.

Então, a fórmula do cubo da diferença é (x – a)(x – a)(x – a) ou (x – a)³. Já o seu resultado será semelhante ao da soma, só que troca o primeiro e o último sinal. Será: x³ – 3x²a + 3xa² – a³.

Então ele pode ser lido assim: “o cubo do primeiro termo, menos três vezes o quadrado do primeiro pelo segundo termo, mais três vezes o primeiro termo pelo quadrado do segundo, menos o cubo do segundo termo.

Exemplo

Pergunta: Se (x – a)³ = x³ – 3x²a + 3xa² – a³, então quanto vale (b – 4)³?

Resposta: b³ – 12b² + 48b – 64

Exercícios de Produtos Notáveis

Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.

Parabéns por ter lido até aqui!

Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.

Questão 1 – (IMNEC – 2004)

A diferença entre o quadrado da soma e o quadrado da diferença entre dois números reais é igual a:

a) a diferença dos quadrados dos dois números.

b) a soma dos quadrados dos dois números.

c) a diferença dos dois números.

d) ao dobro do produto dos números.

e) ao quádruplo do produto dos números.

Questão 2 – Faetec – 2017

Ao entrar na sua sala de aula, Pedro encontrou as seguintes anotações no quadro:

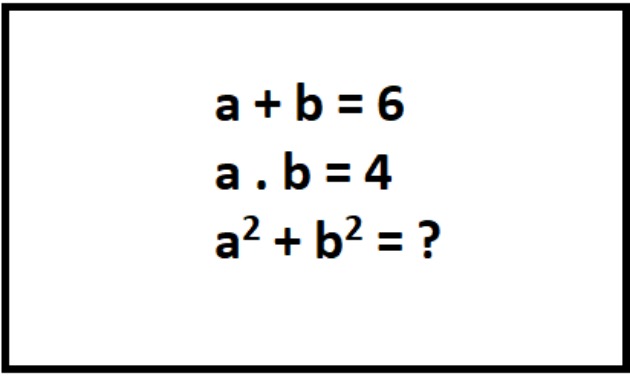
Usando seus conhecimentos sobre produtos notáveis, Pedro determinou corretamente o valor da expressão a2 + b2. Esse valor é:

a) 26.

b) 28.

c) 32.

d)36.

Questão 3 – Cefet/MG – 2017 – Se x e y são dois números reais positivos, então a expressão

a) √xy.

b) 2xy.

c) 4xy.

d) 2√xy.

• Ufa, estamos quase lá! Faça os dois últimos exercícios de Produtos Notáveis!

Questão 4 – Cefet/RJ – 2016

Considere p e q números reais não nulos e não simétricos. A seguir são descritas seis afirmações envolvendo esses números e cada uma delas está associada a um valor informado entre parênteses.

A opção que representa a soma dos valores referentes às afirmações verdadeiras é:

a) 190.

b) 110.

c) 80.

d) 20.

Questão 5 – UFRGS – 2016

Se x + y = 13 e x . y = 1, então x2 + y2 é

a) 166.

b) 167.

c) 168.

d) 169.

e) 170.

• Parabéns, você fez todas as questões sobre Produtos notáveis! Confira o gabarito logo abaixo:

Gabarito dos Exercícios sobre Produtos Notáveis

Exercício resolvido da questão 1 –

Alternativa Correta: e) ao quádruplo do produto dos números.

Exercício resolvido da questão 2 –

Alternativa Correta: b) 28.

Exercício resolvido da questão 3 –

Alternativa Correta: c) 4xy.

Exercício resolvido da questão 4 –

Alternativa Correta: c) 80.

Exercício resolvido da questão 5 –

Alternativa Correta: b) 167.

Gostou dos nossos exercícios de Produtos Notáveis? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, mensalidade e muito mais.

Experimente agora!