Fatorial é apenas uma ferramenta matemática, um símbolo que indica uma operação. Ele é representado por um número inteiro com uma exclamação na frente (n!). O resultado disso é a multiplicação entre todos os antecessores inteiros e positivos de n. Vamos resolver alguns exercícios sobre fatorial para treinar?
Que tal finalmente aprender a resolver os exercícios sobre fatorial? Não é nada complicado e neste artigo vamos explicar tudo passo a passo. Se quiser, clique em um desses tópicos para ir diretamente ao tema:
- O que é fatorial?
- Como fazer simplificação de fatorial?
- Como fazemos operações com fatoriais?
- Exercícios sobre Fatorial
- Gabarito das questões de Fatorial
Quando você terminar os Exercícios sobre Fatorial, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil. É gratuito e é do Beduka para você!
O que é um número fatorial?
Um número fatorial é, na verdade, uma sequência de multiplicações que se inicia no próprio número e se prolonga até o 1. É o produto (resultado) de todos os fatores, começando pelo próprio número e baixando até o 1.
O número fatorial é escrito assim: 6!
6! é o fatorial que desmembrado é o mesmo que 6.5.4.3.2.1, cujo resultado é: 720
(6! = 6.5.4.3.2.1 = 720)
Veja esses outros exemplos, pois esses são números comuns em exercícios sobre fatorial:
5! = 5.4.3.2.1 = 120
4! = 4.3.2.1 = 24
3! = 3.2.1 = 6
2! = 2.1 = 2
Viu como é muito simples? Trata-se apenas de uma sequência de multiplicações com todos os antecessores do número em questão, ou seja, de todos os números menores que ele até o 1.
ATENÇÃO!
- Só existe fatorial de número natural, ou seja, não há fatorial de números negativos ou fracionários, etc.
- Fórmula geral definidora do fatorial: n! = n.(n-1).(n-2).(n-3).(n-4)…3.2.1.
- Por definição matemática temos que 1! = 1 e 0! = 1.
Como fazer simplificação de fatorial?
É muito comum encontrar situações nas quais os exercícios sobre fatorial precisam ser simplificados para serem resolvidos. Simplificar um fatorial é muito simples, basta escolher em qual número você quer parar a sequência.
Exemplo:
5!
5 . 4!
5 . 4 . 3!
5 . 4 . 3 . 2!
Todas as formas acima são diferentes maneiras de se escrever 5!, pois o resultado de todas é 120.
Quando você escolher onde parar a sequência, pode fazer como se vê abaixo:

Equações fatoriais
Bem, o que você esperava? Com certeza os principais exercícios sobre fatorial aparecem em equações. Mas é simples, não precisa se preocupar.
Exemplo: X + 20 = 5!
Basta primeiro resolver o fatorial e depois o restante da equação, logo ela fica assim:
X + 20 = 120
X = 120 – 20
X = 100
Quais operações fazemos com fatoriais?
Aprenda separadamente como realizar cada uma das operações e depois apenas aplique o mesmo nas equações quando estiver resolvendo exercícios sobre fatorial.
Soma ou subtração com fatorial
4! + 3!
(4 . 3 . 2 . 1) + (3 . 2 . 1)
24 + 6 = 30
6! – 4!
(6 . 5 . 4 . 3 . 2 . 1) – (4 . 3 . 2 . 1)
720 – 24 = 696
Multiplicação com fatorial
0! . 5!
1 . (5. 4 . 3 . 2 . 1)
1 . 120 = 120
Divisão com fatorial
Na divisão pode-se realizar a operação resolvendo totalmente o fatorial e depois dividindo-se. Também pode-se fazer pelo método da simplificação como já mostrado. Por uma questão de tempo, caso você esteja fazendo exercícios sobre fatorial no vestibular, é recomendável usar a simplificação.
Exemplo:

O número fatorial aparece na maioria dos problemas de análise combinatória, por isso, é importante treinar com os exercícios sobre fatorial. E fique atento ao nosso blog, pois também postaremos um artigo sobre análise combinatória.
Incógnita no fatorial
O fatorial pode aparecer com letras, mas o processo de simplificação é o mesmo. Basta escrever reduzindo até o formato em que for possível cortar para simplificar.
Veja este caso:
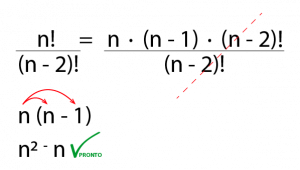
E este:

Perceba, um número negativo diminui quando se distancia de zero e aumenta quando se aproxima, por isso -1 é maior que -2. Logo, se temos n! a forma de fazê-lo é n . (n-1) . (n-2)! etc. Você escolhe onde quer parar para simplificar.
ATENÇÃO: Os exemplos abaixo não são válidos, não cometa esses erros ao fazer exercícios sobre fatorial!
- n! + x! = (n+x)!
- n! – x! = (n-x)!
- n! . x! = (n . x)!
Exercícios sobre Fatorial com Gabarito
Obrigado por ter lido até aqui!
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você. Agora chega de enrolação e vamos às questões sobre Fatorial!
1° dos exercícios sobre Fatorial – (UFF)
O produto 20 x 18 x 16 x 14 x … x 6 x 4 x 2 é equivalente a:
a) 20!/2.
b) 2 . 10!.
c) 20!/210.
d) 210 . 10.
e) 20!/10!.
2° dos exercícios de Fatorial – (UNIFOR)
A soma de todos os números primos que são divisores de 30! é :
a) 140.
b) 139.
c) 132.
d) 130.
e) 129.
3° dos exercícios sobre Fatorial – (Unitau – SP – Adaptada)
Sendo n ≠ 0, assinale a alternativa que possui o(s) valor(es) que satisfaz(em) a equação abaixo:
a) 7.
b) 0 e 7.
c) 0 e 10.
d) 1.
e) 0 e 2.
- Ufa, estamos quase no fim. Faça os 2 últimos exercícios de Fatorial.
4° dos exercícios de Fatorial – (Unifor–CE)
Um casal e seus quatro filhos vão ser colocados lado a lado para tirar uma foto. Se todos os filhos devem ficar entre os pais, de quantos modos distintos os seis podem posar para tirar a foto?
a) 24.
b) 48.
c) 96.
d) 120.
e) 720.
5° dos exercícios sobre Fatorial – (ITA–SP)
Quantos números de seis algarismos distintos podemos formar usando os dígitos 1, 2, 3, 4, 5 e 6, nos quais o 1 e o 2 nunca ocupam posições adjacentes (juntos), mas o 3 e o 4 sempre ocupam posições adjacentes?
a) 144.
b) 180.
c) 240.
d) 288.
e) 360.
- Parabéns, você fez todos as questões sobre Fatorial, confira agora o Gabarito:
Gabarito das questões de Fatorial
Exercício resolvido da questão 1 –
Alternativa correta: d) 210 . 10.
Exercício resolvido da questão 2 –
Alternativa correta: e) 129.
Exercício resolvido da questão 3 –
Alternativa correta: a) 7.
Exercício resolvido da questão 4 –
Alternativa correta: b) 48 (2 * 4! = 48).
Exercício resolvido da questão 5 –
Alternativa correta: a) 14.
Curtiu os nossos exercícios sobre Fatorial? Então siga o Beduka no Instagram para conteúdos diários. Lá é cheio de dicas e resumos para ajudar os vestibulandos e demais estudantes!






8 Comentários
A questão ta errada, o correto seria 2^10 * 10 !
Obrigado pelo alerta Davi.
A resposta está correta agora.
Obrigado pelo post,me salvou na questão.
Não foi nada, Marcos. Ficamos felizes em ajudar.
Olá! Por favor, me ajudem com essa questão:
Entre os números a seguir, o único que é um quadrado perfeito é:
A) ( 14! 15! ) ÷ 2
B) ( 15! 16! ) ÷ 2
C) ( 16! 17! ) ÷ 2
D) ( 17! 18! ) ÷ 2
E) ( 18! 19! ) ÷ 2
Essa questão caiu no concurso. A resposta certa é a letra D.
Por que a resposta certa é a letra D?
Mandem a resolução para meu e-mail, por favor.
Desde já, muito obrigado.
José, a resposta é D porque aplicando a simplificação de fatoriais, todos vão dar em algum resultado, mas o único que terá raiz exata é o da letra D.
Entenda que se um numero inteiro vezes x ele próprio resulta num quadrado perfeito, basta perceber que
na letra a vc teria 14! ao quadrado vezes 7,5
Na letra b vc teria 15! ao quadrado vezes 8
Na letra c vc teria 16! ao quadrado vezes 8,5
Na letra d vc teria 16! ao quadrado vezes 9
Na letra e vc teria 18! ao quadrado vezes 9,5.
Portanto, como 9 é quadrado perfeito, essa é a resposta
Isso, professora. Muito obrigado!