Os 7 Melhores Exercícios sobre Números Complexos com Gabarito

Os números complexos são representados de 3 formas: a forma geométrica (representada no plano complexo conhecido como plano de Argand-Gauss, a forma trigonométrica, conhecida como forma polar e a forma algébrica (z = a + b), composta por uma parte real “a” e uma parte imaginária “b”. Leia nosso resumo e faça os 8 Melhores Exercícios sobre Números Complexos.

Quando você terminar os 8 Melhores Exercícios sobre Números Complexos, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil. 

Estudar números complexos não é uma tarefa fácil. Eles não são complexos apenas no nome… Calma!

Nós sabemos que você não tem tempo para enrolações, certo? Então vamos direto ao ponto:

Escrevemos um resumo que lhe passará uma matéria difícil de maneira mais simples e, ao final, ainda lhe daremos a oportunidade de fazer Os 10 Melhores Exercícios sobre Números Complexos.

Não é um milagre, mas já é uma mão na roda, né?

Então se gostou da ideia, leia este artigo até o final.

• Sabia que os números complexos é um dos assuntos que mais caem na prova da Fuvest?

O que é um Número Complexo?

Os números complexos são representados de 3 formas: a forma geométrica (representada no plano complexo conhecido como plano de Argand-Gauss), a forma trigonométrica, conhecida como forma polar e a forma algébrica (z = a + b), composta por uma parte real “a” e uma parte imaginária “b”.

Os números complexos surgiram a partir da necessidade de resolver equações que possuem raízes de números negativos. Podendo ser expresso de diferentes formas.

Eles possuem operações bem definidas: 

• subtração;
• multiplicação; 
• divisão;
• potencialização.

Forma algébrica de um número complexo (z = a + b)

Antigamente, quando tentávamos resolver uma operação do segundo grau, como X² = -16, considerávamos ela sem solução. Isso mudou…

Com o surgimento dos números complexos e da possibilidade de representá-los algebricamente, tornou-se possível a realização desse tipo de operação.

Para possibilitar a resolução das situações em que se trabalha com a raiz quadrada de um número negativo, foi determinada a unidade imaginária:

i = -1

Então, analisando- a equação apresentada em x² = -16, temos que:

X² = -16

X = +/- -16

X = +/- 16 . (-1)

X = +/- (16. -1)

X = +/- 4i

Sendo assim, as soluções para esta equação são -4i e 4i

• Relembre tudo sobre Equação do 2° Grau

Estrutura de um Número Complexo 

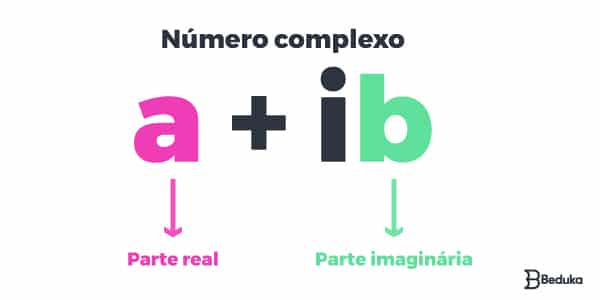
Sendo que:

• a e b são números reais.
• a: parte real, indicada por a = Re(z);
• b: parte imaginária, indicada por Im(z);
• i: unidade imaginária.

Adição entre Números Complexos

Tendo em mente dois números complexos (T₁ e T₂), faremos a adição da parte imaginária e depois a adição da parte real entre eles, observe:

T₁ = a + bi

T₂ = c + di

T₁ +T₂ = (a + c) + (b + d)i

Subtração entre Números Complexos

Tendo em mente dois números complexos (T₁ e T₂), faremos a subtração da parte imaginária e depois a subtração da parte real entre eles, observe:

Realização da subtração de T₁ e T₂.

T₁ = 2 + 3i

T₂ = 1 + 2i

T₁ –T₂ = (2 – 1) + (3 – 2)i

T₁ –T₂ = 1 + 1i = 1+ i

Potência da Unidade Imaginária

Para encontrarmos uma potência da unidade i ⁿ, faremos a divisão de n (o expoente) por 4, e o resto dessa divisão (r = { 0, 1, 2, 3}) será o novo expoente de i. Observe:

Cálculo de i²⁵

Ao resolvermos a divisão de 25 por 4, o quociente será 6 e o resto será igual a 1. Logo:

i ²⁵ = i¹ = i

Multiplicação de Números Complexos 

Antes de resolvermos a multiplicação é preciso entender a propriedade distributiva. Observe:

T₁ = a + bi

T₂ = c +di, então o produto:

T₁ · T₂ = (a + bi) (c + di), aplicando a propriedade distributiva,

T₁ · T₂ = ac + adi + cbi + bdi ², mas, como vimos, i ² = -1

T₁ · T₂ = ac + adi + cbi – bd

T₁ · T₂ = (ac – bd) + (ad + cb)i

A partir disso, é possível encontrarmos o produto de quaisquer números complexos. 

Não é preciso decorar essa fórmula, já que, para o cálculo em questão, basta aplicarmos a propriedade distributiva. Entenda melhor com um exemplo:

Calcule o produto de (2+3i) (1 – 4i):

(2+3i) (1 – 4i) = 2 – 8i + 3i – 12i ², lembrando que i² = -1:

(2 + 3i) (1 – 4i) = 2 – 8i + 3i + 12

(2 + 3i) (1 – 4i) = (2 + 12) + (– 8 + 3)i

(2+3i) (1 – 4i) = 14 – 5i

Divisão de Números Complexos

Multiplique a fração pelo conjugado do denominador para que fique bem definido o que é a parte real e o que é a parte imaginária.

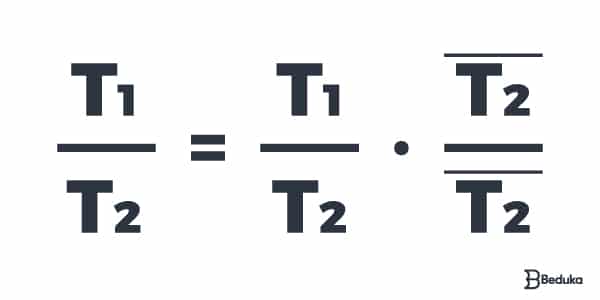
Para encontrarmos o conjugado de um número complexo, trocamos o sinal da parte imaginária. Sendo assim:

T = a + bi → T = a – bi

Calcule a divisão de (6 – 4i) : (4 + 2i)

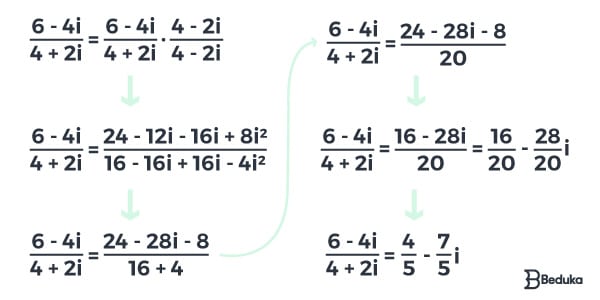
Plano complexo ou plano de Argand-Gauss (Forma Geométrica)

Esse plano é uma adaptação do plano cartesiano com o objetivo de representar números complexos

• Re (z): eixo da parte real;
• Im (z): eixo da parte imaginária;

Representação do número 4 + 3i na forma geométrica T(4,3).

• ENTENDA TUDO SOBRE GEOMETRIA!

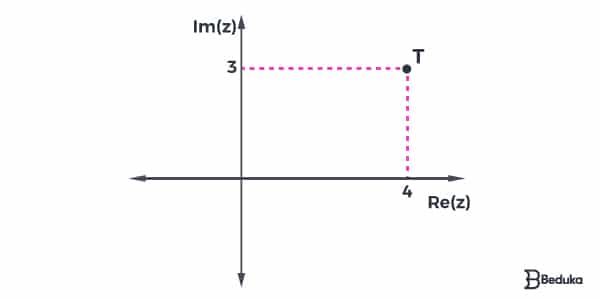
Representação Trigonométrica dos Números Complexos (Forma Polar)

A partir da forma algébrica z = a + bi, iremos analisar o plano complexo:

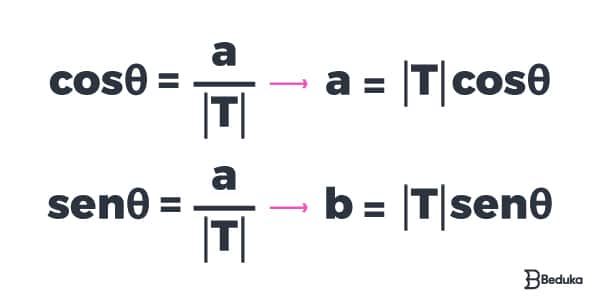
Ao substituirmos, na forma algébrica, os valores de a = |T| cos θ e b = |T| sen θ, temos que:

T = a + bi

Com T = |T| cos θ + |T| sen θ · i, colocando |T| em evidência, chegamos à fórmula da forma trigonométrica:

• É essencial conhecer bastante sobre Trigonometria para mandar bem nos Exercícios sobre Números Complexos

Exercícios sobre Números Complexos com Gabarito

Esperamos que, com esse resumo, tudo tenha ficado mais claro para você. 

Parabéns por ter lido até aqui!

Questão 1 – (Unesp-SP) Se z = (2 + i) ∙ (1 + i) ∙ i, então z, o conjugado de z, será dado por:

a) −3 − i

b) 1 − 3i

c) 3 − i

d) −3 + i

e) 3 + i

Questão 2 – (PUC) Na soma S = 1 + i + i² + i³ + i⁴ + i⁵, onde i = √ –1, o valor de S é:

a) 2 – i

b) 1 – i

c) 2 + i

d) 1 + i

Questão 3 – (UFU 2008) Considere o triângulo cujos vértices correspondem aos números complexos z1= 3, z2= 6 e z3=8+3i, em que i é a unidade imaginária. Sabe-se que outro triângulo de vértices correspondentes a w1 = –iz1, w2 = –iz2 e w3 = –ihz3, sendo h um número real positivo, possui área igual a 18. Então, o valor de h é igual a:

a) 10

b) 6

c) 8

d) 4

• Você está indo muito bem! Chegamos à metade dos Exercícios sobre Números Complexos.

Questão 4 – (UEA 2005) Qual é o conjunto das imagens dos complexos z tais que |z + 1| = |z – 1|?

a) reta

b) circunferência

c) elipse

d) hipérbole

e) parábola

Questão 5 – (FURG) Se u = 1 – 2i é um número complexo e U, seu conjugado, então z = u2 + 3U é igual a:

a) – 6 – 2i

b) 2i

c) – 6

d) 8 + 2i

e) – 6 + 2i

• Ufa! Estamos quase no fim, continue e faça o último exercícios sobre Números Complexos

Questão 6 – (UEFS) Se m – 1 + ni = (3 + i).(1 + 3i), então m e n são respectivamente:

a) 1 e 10      

b) 5 e 10       

c) 7 e 9      

d) 5 e 9      

e) 0 e -9

Questão 7 – (UEFS) A soma de um número complexo z com o triplo do seu conjugado é igual a -8 – 6i. O módulo de z é:

a) Ö13      

b) Ö7       

c) 13      

d) 7     

e) 5

• Parabéns, chegou ao fim dos Exercícios sobre Números Complexos. Confira agora o Gabarito:

Gabarito dos Exercícios sobre Números Complexos

Exercício resolvido da questão 1 –

Alternativa correta: a) −3 − i 

Exercício resolvido da questão 2 –

Alternativa correta: d) 1 + i

Exercício resolvido da questão 3 –

Alternativa correta: d) 4

Exercício resolvido da questão 4 –

Alternativa correta: a) reta

Exercício resolvido da questão 5 –

Alternativa correta: b) 2i

Exercício resolvido da questão 6 –

Alternativa correta: a) 1 e 10   

Exercício resolvido da questão 7 –

Alternativa correta: a) Ö13 

Estude para o Enem com o Simulado Beduka. É gratuito!

Gostou dos nossos Exercícios sobre Números Complexos? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.