Números Complexos são aqueles que estão além do conjunto dos Números Reais. Eles foram desenvolvidos para ajudar no cálculo de raízes de números negativos, como na resolução de uma equação de segundo grau. Eles podem ser representados pela forma polar, geométrica ou algébrica que possui a unidade imaginária “i” de valor √-1.
Neste artigo sobre o que são números complexos, você encontrará:
- O que são números complexos – Exemplos
- Para que servem os números complexos
- História do conjunto dos números complexos
- Operações com os números complexos: soma, subtração, divisão e multiplicação
- Depois de ler o artigo, treine com os exercícios de números complexos!
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que são números complexos – Exemplos
Os números Complexos fazem parte de um dos conjuntos numéricos, caracterizados por exceder os dos números Reais.
Pode ser um pouco difícil tentar compreender isso, pois na escola crescemos utilizando apenas os números Naturais (1,2,3…), os Inteiros (-1, -2, 4, 5…), os Racionais
(½ , 0.75…) e os Irracionais ( π, e, …).
Todos os citados acima fazem parte dos números Reais, então, o que seriam os Complexos?
Eles costumam ser definidos pela forma algébrica z = a + bi. Vamos entendê-la:
Forma algébrica
Os números complexos são expressos pelo símbolo “z” que é, na verdade, uma expressão algébrica:
- z = a + bi
Sendo assim, temos:
- a → é a parte real porque contém um número Real sozinho, assim é simbolizada por “a = Re(z)”
- b → é um elemento da parte imaginária porque o b é número Real que multiplica o “i”, sendo indicada por “Im(z)”
- i → chama-se unidade imaginária, um recurso que foi criado para resolução de cálculos. O seu valor é i = √– 1.
Exemplos numéricos:
- 2 + 3i
- -1 + 4i
- 5 – 0,2i
- -1 – 3i
Quando a parte real é nula, o número é conhecido como imaginário puro.
Exemplos: –5i, 3i e 7,8i.
Mas, quando a parte imaginária é nula, o número Complexo é também um número Real.
Exemplo: 5 , que veio de “5 + 0.i”.
Forma geométrica (plano cartesiano)
Na matemática existem diversas formas de expressar quantidade, seja pela álgebra ou pela geometria. Aqui iremos representar a mesma coisa que foi dita anteriormente, mas em uma linguagem traduzida para o plano cartesiano.
Como a e b são números reais, eles já eram considerados pontos de um plano cartesiano. Neste caso é conhecido como plano de Argand-Gauss, pois expressa quantidades que estão além dos Reais, como o “i” que é dos Complexos.
O plano cartesiano é definido por duas retas ortogonais, ou seja, que fazem um ângulo reto (90°) entre si. Essas retas são conhecidas como eixos x (horizontal, abscissas) e y (vertical, ordenadas).
Os números Reais são representados de forma que nas retas colocamos os números Racionais e os espaços restantes entre os pontos das retas são preenchidos com os Irracionais.
Assim, todos os outros pontos pertencentes a esse plano, e que não estão nas retas, são a diferença entre os números Complexos e os Reais.
Por isso fica evidente que o conjunto dos números Reais está contido no conjunto dos números Complexos, bem como os dos Naturais está contido nos dos Inteiros, ainda que mantenham suas diferenças.
Forma trigonométrica ou polar
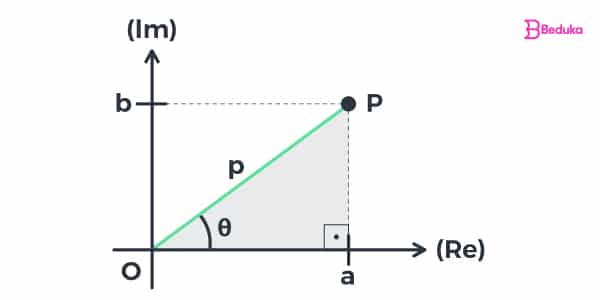
Essa terceira forma de representar os números Complexos utiliza o módulo, ou seja, quando um número é representado entre duas barras e tem como resultado sempre o “positivo” desse número.
Na realidade, ele expressa o valor absoluto, a quantia em si, sendo a distância entre o número posicionado e a origem (0).
Exemplo: |5| = 5 e |-5| = 5 .
Como no plano cartesiano o número Complexo Z não faz parte da reta, a sua distância até o centro (para obter o módulo) será calculado pelo ângulo da reta que liga a localização do ponto Z à origem.
Por esse motivo, o número complexo Z pode ser representado com a forma polar por:
- Z = |Z|·(cosθ + icosθ)
Esqueceu o que é “cos”? Confira a nossa matéria de trigonometria!
História do conjunto dos números complexos

Mas de onde surgiu tudo isso? Bem, em 1572 Rafael Bombelli tentava resolver algumas equações de segundo grau e se deparou com uma em que o discriminante era negativo.
Ele viu que não fazia sentido calcular a raiz quadrada de um número negativo, pois a sua conta oposta é a exponenciação ao quadrado e, independe do sinal da base, ter um expoente par sempre resulta positivo. Veja:
(-2)² = 4 (-2 . -2) e 2² = 4 (2 . 2)
Então √4 = 2 ou -2.
A única forma de obter um resultado negativo ao multiplicar dois números, é se eles forem opostos, como “-2” e “2”. Mas aí já não cabe no conceito de exponenciação e raíz, pois eles levam em conta a multiplicação de um número por ele mesmo.
Por isso, teve a ideia de supor que √– 121 poderia ser representado como √(– 11·11), decompondo o número. Continuando a conta utilizando a ideia de fator comum, teremos 11·√– 1.
Esse tipo de operação deveria receber um novo nome porque não se enquadrava em nada visto antes e era uma forma de “raiz não real”. Se continuarmos aplicando essa técnica em outras raízes, sempre restará a sua raiz real seguida pela multiplicação do “√– 1”, veja:
√-100 = √ -10 . 10 = 10 √-1
√-25 = √ -5 . 5 = 5 √-1
√-625 = √ -25 . 25 = 25 √-1
Por isso, decidiram chamar o √– 1 de “i”. Dessa forma chegamos à fórmula algébrica já estudada : z = a + bi. Nos casos acima o “a” vale 0, o “b” seria o resultado da raiz real e o “i” indica que na verdade veio de uma raíz não real, negativa.
Somente no final do século XVIII que Gauss chamou esse conjunto de números como “Números Complexos”.
Para que servem os números complexos?
Com base em toda essa explicação, você já deve ter entendido que os números complexos servem para auxiliar na resolução de equações de segundo grau cujo determinante resulta negativo.
Até meados do século XVI, equações como x2 – 6x + 10 = 0 eram consideradas como “sem solução”. Agora é possível ter uma noção de algo próximo ao resultado, ainda que não seja Real.
Operações com os números complexos
Como estamos trabalhando com um conjunto numérico, os números complexos também possuem as 4 operações básicas bem definidas: adição, subtração, multiplicação, divisão.
Agora que você já sabe o que são números complexos, vamos entender as operações!
Adição de números complexos
Para realizarmos a adição de dois números complexos Z1 e Z2, basta fazer a soma da parte real e depois a soma da parte imaginária.
- Exemplo algébrico:
Seja Z1 = a + bi e Z2 = c + di
Teremos que Z1 + Z2 = (a + c) + (b + d)i
- Exemplo numérico:
Seja Z1 = 2 + 3i e Z2 = 1 + 2i
Teremos que Z1 + Z2 = (2 + 1) + (3 + 2)i
Então = 3 + 5i
Subtração de números complexos
Antes, precisamos ter em mente que o inverso de z é representado por –Z, ou seja, –Z = –a – bi.
Para realizarmos a subtração entre Z1 e Z2, faremos a subtração entre as partes reais e as imaginárias separadamente. Porém, é necessário compreender que –Z2 é o inverso de um número complexo, o que torna necessário a realização de um jogo de sinal.
- Exemplo numérico
Seja Z1 = 2 + 3i e Z2 = 1 + 2i
Teremos que Z1 – Z2 = (2 – 1) + ( 3 – 2)i
Então Z1 – Z2 = 1 + 1i , ou seja, 1+ i
Divisão de números complexos
Antes de falarmos de divisão, precisamos saber o que é conjugado de um número. O conceito é simples: para encontrar o conjugado basta trocar o sinal da parte imaginária.
Divisão de números complexos
Para realizar a divisão de números complexos, multiplique numerador e denominador pelo conjugado do denominador. Assim fica bem definido o que é a parte real e o que é a parte imaginária.
- Exemplo numérico
Se (6 – 4i) : (4 + 2i)
Então (6 – 4i)(4 – 2i)/ (4 + 2i)(4 – 2i)
24 – 12i – 16i +8i² / 16 -8i +8i -4i²
Sabendo que i² = -1, então 24 -38i – 8 / 16 +4
16 – 38i / 20
Multiplicação de números complexos
Antes de falarmos da multiplicação, precisamos entender que as potências da unidade imaginária comportam-se de forma cíclica. Veja:
i^4 = i^2 · i^2 = (–1) . (–1) = 1
i^5 = i 2 · i 3 = (–1) (–i) = i
Se você continuar calculando as potências, as respostas sempre serão elementos do conjunto {i, 1, –i,–1}, de forma alternada.
Por causa desses ciclos, para encontrarmos uma potência de base “i”, basta dividir o número do expoente por 4 (só há 4 resultados possíveis). O resto dessa divisão será o novo expoente de i.
- Exemplo numérico
Para saber quanto é i^25 basta fazer 25/4. O resto é 1, logo, i^25 = i^1. Sabemos que todo número elevado a 1 é ele mesmo, então i^25 = i.
Para saber quanto é i^403 basta fazer 403/4. O resto é 3, logo, i^403 = i^3. Assim, temos que i^3 = -i.
Multiplicação de números complexos
Para realizarmos a multiplicação de dois números complexos, vamos aplicar a propriedade distributiva.
- Exemplo algébrico
Seja Z1 = a + bi e Z2 = c +di
Então o produto Z1 · Z2 = (a + bi) (c + di)
Aplicando a propriedade distributiva temos Z1 · Z2 = ac + adi + cbi + bd.i²
Como vimos nas potências, i ² = -1, então: Z1 · Z2 = ac + adi + cbi – bd
Utilizando fato comum chegamos à Z1 · Z2 = (ac – bd) + (ad + cb)i
Se você decorar apenas essa última fórmula, conseguirá encontrar o produto de qualquer número complexo. Mas, de modo geral, ela não precisa ser decorada porque basta aplicarmos a propriedade distributiva e o fator comum!
- Exemplo numérico
Cálculo do produto de (2+3i) (1 – 4i) = 2 – 8i + 3i – 12i ²
Lembrando que i² = -1, teremos (2 + 3i) (1 – 4i) = 2 – 8i + 3i + 12
(2 + 3i) (1 – 4i) = (2 + 12) + (– 8 + 3)i
(2+3i) (1 – 4i) = 14 – 5i
Gostou do nosso artigo sobre o que são números complexos? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!







