As razões trigonométricas são um estudo da matemática capaz de relacionar determinados ângulos de um triângulo retângulo e suas medidas, lados. Faça os Exercícios sobre Razões Trigonométricas para testar os seus conhecimentos sobre o assunto.
A matéria de Razões Trigonométricas é cobrada na prova de Matemática e suas Tecnologias no Enem, na parte de matemática. Por isso fazer os exercícios sobre razões trigonométricas e revisar a matéria vai te preparar ainda mais para os principais vestibulares.
Razões Trigonométricas
As razões trigonométricas são essenciais para a trigonometria e são obtidas pelas dimensões dos lados de um triângulo retângulo, lembrando que o triângulo só é retângulo quando um dos ângulos é reto, tem 90º.
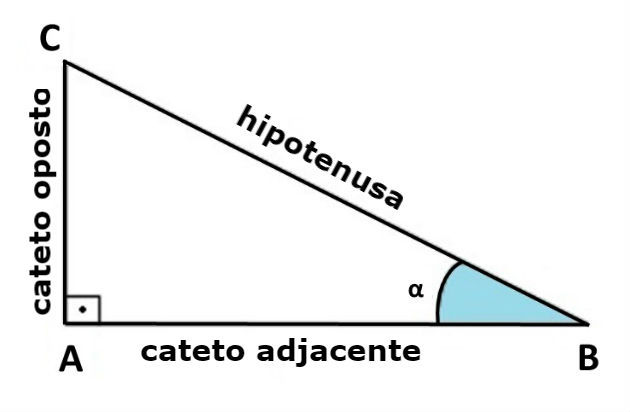
A trigonometria surgiu por causa da necessidade do homem em relacionar ângulos a distâncias difíceis de serem acessíveis. O triângulo foi uma peça essencial para o desenvolvimento da trigonometria, pois a partir dele relações particulares entre os ângulos e a medida dos lados conseguiram ser ditas.
O estudo da trigonometria foi denominado de razões trigonométricas, sendo definidas como seno, cosseno e tangente. As razões trigonométricas são utilizadas no triângulo retângulo, veja a representação na imagem abaixo:
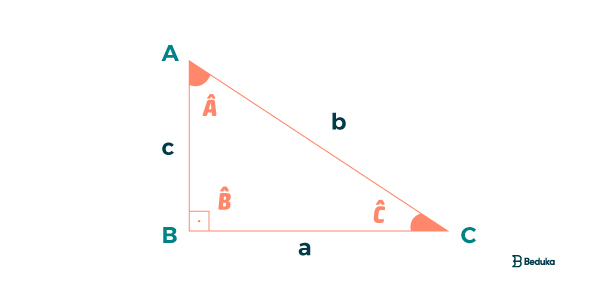
O ângulo “b” tem 90º, já os lados dos ângulos “a” e “c”são denominados de catetos e o oposto ao ângulo reto é definido como hipotenusa, o maior lado do triângulo retângulo.
Assim, se imaginarmos que temos o ângulo ”a“ como referência, será oposto ao cateto ”a“ e será adjacente ao cateto “c”. O cálculo do seno e cosseno é a razão entre o cateto oposto e o cateto adjacente com a hipotenusa, já a tangente é então a razão entre o seno e o cosseno.
Saiba como aprender geometria!
Agora é a sua vez de fazer os Exercícios sobre Razões Trigonométricas e testar os seus conhecimentos sobre o assunto.
Exercícios sobre Razões Trigonométricas
Baixe o melhor plano de estudos gratuito que você encontrará na internet.
1 – (Cesgranrio) – Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:
a) 6√3 m.
b) 12 m.
c) 13,6 m.
d) 9√3 m.
e) 18 m.
2 – (UFAM)- Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente, então a tangente do ângulo oposto ao menor lado é:
a) 2√3
b) √3
3
c) √3
6
d) √20
20
3 – (ENEM 2013) – As torres Puerta de Europa são duas torres inclinadas uma contra a outra, construídas numa avenida de Madri, na Espanha. A inclinação das torres é de 15° com a vertical e elas têm, cada uma, uma altura de 114 m (a altura é indicada na figura como o segmento AB). Estas torres são um bom exemplo de um prisma oblíquo de base quadrada e uma delas pode ser observada na imagem.

1ª questão com seno, cosseno e tangente – Enem 2013
Disponível em: www.flickr.com. Acesso em: 27 mar. 2012.
Utilizando 0,26 como valor aproximado para a tangente de 15° e duas casas decimais nas operações, descobre-se que a área da base desse prédio ocupa na avenida um espaço:
a) menor que 100m².
b) entre 100 m² e 300 m².
c) entre 300 m² e 500 m².
d) entre 500 m² e 700 m².
e) maior que 700 m².
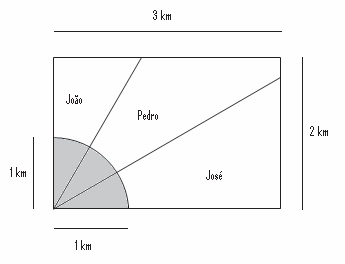
4 – (ENEM 2009) – Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular de 3 km x 2 km que contém uma área de extração de ouro delimitada por um quarto de círculo de raio 1 km a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro, os irmãos acordaram em repartir a propriedade de modo que cada um ficasse com a terça parte da área de extração, conforme mostra a figura.
2ª questão com seno, cosseno e tangente – Enem 2013
Em relação à partilha proposta, constata-se que a porcentagem da área do terreno que coube a João corresponde, aproximadamente, a
(Considere = 0,58)
a) 50%
b) 43%
c) 37%
d) 33%
e) 19%
5 – (Cesgranrio) – Uma escada de 2m de comprimento está apoiada no chão e em uma parede vertical. Se a escada faz 30° com a horizontal, a distância do topo da escada ao chão é de:
a) 0,5 m
b) 1 m
c) 1,5 m
d) 1,7 m
e) 2 m
6– (Ufjf) – A uma tela de computador está associado um sistema de coordenadas cartesianas, com origem no canto inferior esquerdo. Um certo programa gráfico pode ser usado para desenhar na tela somente retas de inclinações iguais a 0°, 30°, 45°, 60° e 90° em relação ao eixo horizontal. Então, considerando-se os pontos a seguir, o único que NÃO pode estar sobre uma reta, A PARTIR DA ORIGEM, desenhada por este programa é:
a) (0, 10Ë3).
b) (10Ë3, 0).
c) (10Ë3, 10Ë3).
d) (10Ë3, 5Ë3).
e) (10Ë3, 10).
7 – (Ufes) – Duas circunferências são tangentes entre si e aos lados de um ângulo. Se R é o raio da maior, r é o raio da menor e o ângulo mede 60°, então
a) R = (3Ë3)r/2
b) R = 2Ë3r
c) R = 3Ë3r
d) R = 2r
e) R = 3r
Respostas dos Exercícios sobre Razões Trigonométricas
Exercício resolvido da questão 1 –
e) 18 m.
Exercício resolvido da questão 2 –
b) √3
3
Exercício resolvido da questão 3 –
e) maior que 700 m².
Exercício resolvido da questão 4 –
e) 19%
Exercício resolvido da questão 5 –
b) 1 m
Exercício resolvido da questão 6 –
d) (10Ë3, 5Ë3).
Exercício resolvido da questão 7 –
e) R = 3r
Estude para o Enem com o Simulado Enem do Beduka. É gratuito!
Gostou dos nossos Exercícios sobre Razões Trigonométricas? Compartilhe com os seus amigos e comente abaixo sobre áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





